2017-2018-1 20155327 《信息安全系统设计基础》第十三周学习总结
本章要点
程序的机器级表示
计算机执行机器代码,用字节序列编码低级操作,包括处理数据、管理储存器、读写储存设备上的数据,以及利用网络通信。
3.1历史观点
Intel处理器俗称X86,经历了长期的、不断进化的发展过程。
3.2程序编码
编译代码:
gcc =O1 -o p p1.c p2.c
实际上gcc命令调用了一系列程序,将源代码转化成可执行代码。
3.2.1机器级代码
指令集体系结构ISA:定义了处理器状态、指令的格式,每条指令对状态的影响。
3.3数据格式
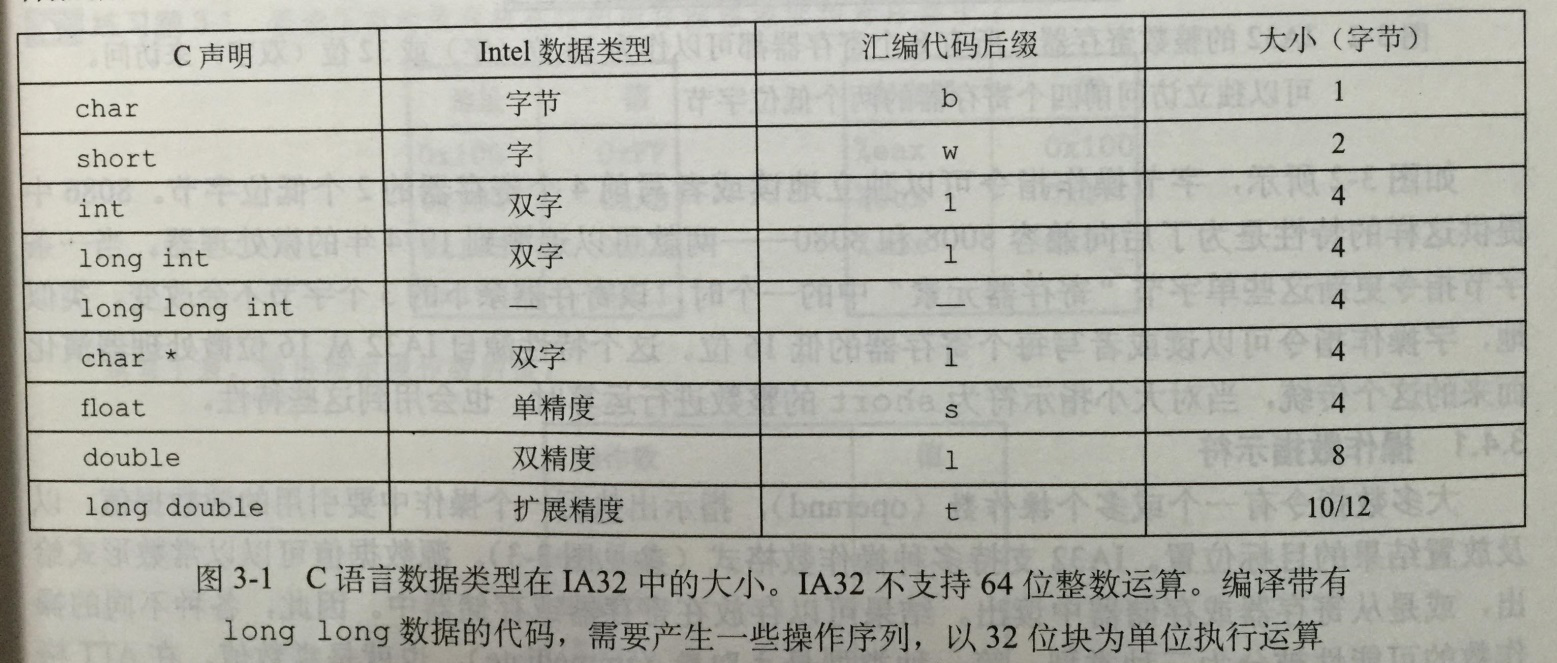
3.4访问信息
一个IA32中央处理单元包含一组8个储存32位值的寄存器。这些寄存器用来存储整数数据和指针。
3.4.1操作数指示符
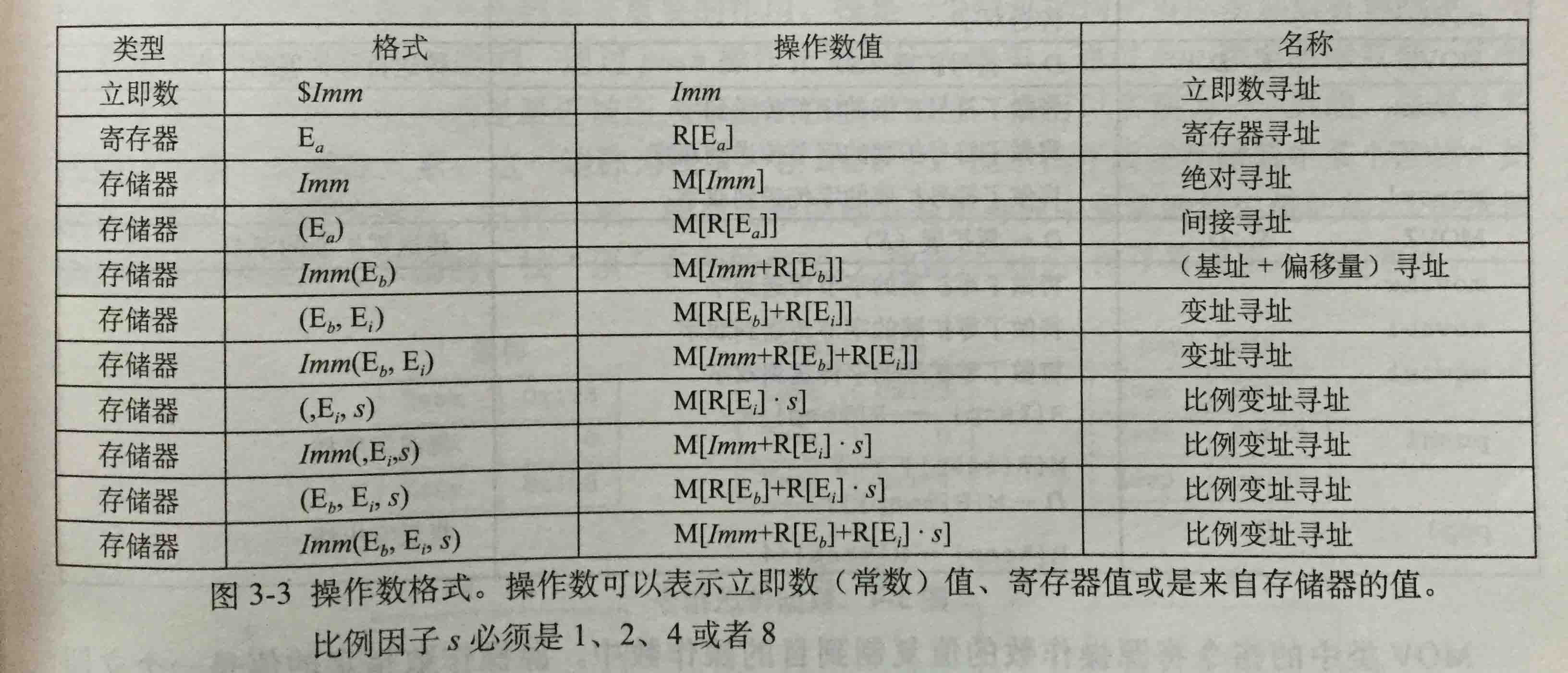
3.4.2数据传送指令
将数据从一个位置复制到另一个位置的指令。
3.4.3数据传送指令:
MOV:movb,movw,movl分别传送字节,字,双字
MOVZ(零扩展,高位用0填充):同上,压栈出栈见p114表格。(注意栈顶的地址值是栈中最小的)
MOVS(符号扩展,高位用原来最高位的数值填充):同上
C语言中,指针就是地址,间接引用指针就是将指针放在一个寄存器中,然后在存储器中使用这个寄存器。
3.5算数和逻辑操作
四种整数操作:
加载有效地址:实际是将有效地址写入目的操作数,目的操作数必须是寄存器。
一元操作:只有一个操作数,可以是寄存器也可是存储器位置。
二元操作:源操作数是第一个,可以是立即数、寄存器、存储器 目的操作数是第二个,可以是寄存器、存储器 两个不能同时为存储器。
移位:第一个是移位量,用单个字节编码(只允许0-31位的移位)。
3.6控制
控制中最核心的是跳转语句:
有条件跳转
无条件跳转
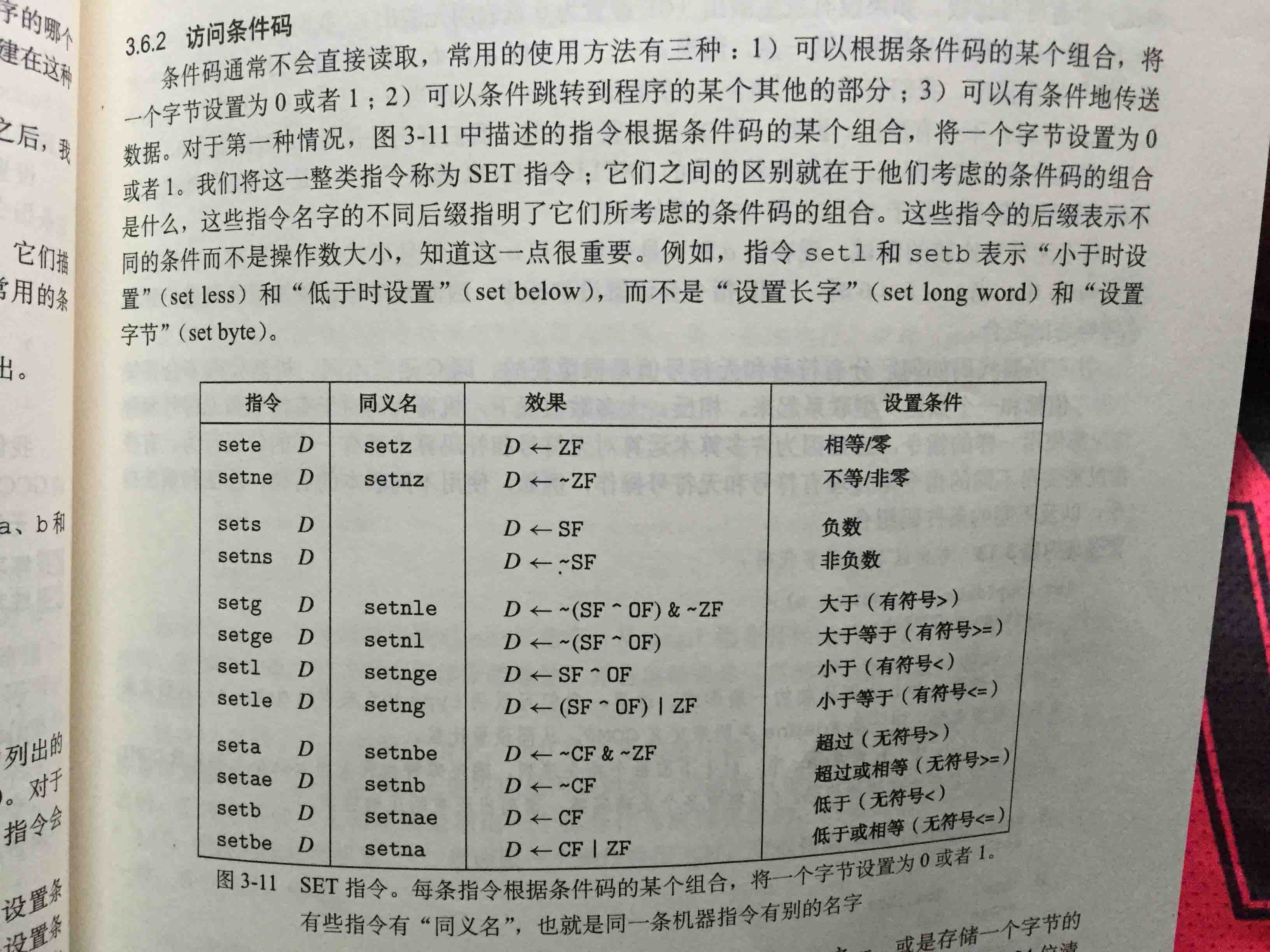
3.6.5循环
1.do-while循环
通用形式:
body-statement
while(test-expr);
loop:
body-statement
t = test-expr;
if(t)
goto loop;````
2.while循环
通用形式:
````while (test-expr)
body-statement
if(!test-expr)
goto done;
do
body-statement
while(test-expr);````
3.for循环
通用形式:
````for(init-expr;test-expr;update-expr)
body-satament
3.7过程
过程可以理解为c中的函数,当调用者(caller)调用被调用者(be caller)的时候,系统会为被调用者在栈内分配空间,这个空间就称为栈帧。栈顶元素的地址是所有栈中元素地址中最低的
栈用来传递参数、存储返回信息、保存寄存器,以及本地存储。
栈帧:为单个过程分配的那部分栈称为栈帧。
最顶端的栈帧以两个指针界定:
寄存器%ebp-帧指针
寄存器%esp-栈指针
本章习题
*3.58
decode2:
subq %rdx, %rsi # %rsi = y - z;
imulq %rsi, %rdi # %rdi = (y - z) * x;
movq %rsi, %rax # %rax = y - z;
salq $63, %rax # %rax = (y - z) << 63;
sarq $63, %rax # %rax = ((y - z) << 63) >> 63;
xorq %rdi, %rax # %rax=(((y - z) << 63) >> 63) ^ ((y - z) * x)
ret
相应的C代码为(((y-z)<<63)>>63)^((y-z)*x)
**3.59
- %rdx与%rax共同代表一个128位数的意思,是指用可以用计算公式%rdx*2^64+%rax来表示这个数,而并不是把这%rdx和%rax的二进制串串连起来表示这个数,区别在于,当这个数为负数的时候,%rdx是-1.意思是所有位都为1,而如果串连起来的话,显然只有%rdx的第一位为1,后面全为0.因此这里的数学公式推理才正确,所以对于汇编的第10行为什么要加上%rcx,就不要用串连起来的表示方法去想象这一行的正确性,而应该用数学公式去推.
下面用x0,y0来分别表示x和y的低位,用x1,y1来分别表示x和y的高位,用W表示2^64,因此下面的公式成立:
p = x * y
= (x1*W + x0) * (y1*W + y0)
= (x1*y1*W*W) + W(x1*y0+x0*y1) + x0*y0
公式中x1y1WW超过了128位,而且未超出128位部分始终全为0,因此可以去掉.于是公式变成了p=W(x1y0+x0y1) + x0y0,然后可以继续转化,注意这里的x0y0是很可能会超出64位的,假设x0y0的超出64位的部分为z1,未超出64位的部分为z0.那么公式可以变成如下:
p = W(x1*y0+x0*y1+z1) + z0
很明显,需要将x1y0+x0y1+z1放到最终结果的高位,即(%rdi),z0放到最终结果的低位,即8(%rdi)
然后仔细翻译下各个语句
store_prod:
movq %rdx, %rax # %rax = y0.
cqto # 有符号运算,因此用cqto,这里会自动关联%rdx和%rax分别表示高位和低位,假如y是负数,那么%rdx所有位都是1(此时值是-1),否则,%rdx全为0, %rdx = y1.
movq %rsi, %rcx # %rcx = x0.
sarq $63, %rcx # 将%rcx向右移63位,跟%rdx的含义一样,要么是-1,要么是0, %rcx = x1.
imulq %rax, %rcx # %rcx = y0 * x1
imulq %rsi, %rdx # %rdx = x0 * y1
addq %rdx, %rcx # %rcx = y0 * x1 + x0 * y1
mulq %rsi # 无符号计算 x0*y0,并将x0*y0的128位结果的高位放在%rdx,低位放在%rax,因此这里%rdx = z1, %rax = z0.
addq %rcx, %rdx # %rdx = y0*x1+x0*y1+z1
movq %rax, (%rdi) # 将%rax的值放到结果的低位
movq %rdx, 8(%rdi)# 将%rdx的值放到结果的高位,可以发现跟上面用数学公式推理的结果完全一致!!!!
ret
1
**3.60
loop:
movl %esi, %ecx # %ecx=n;
movl $1, %edx # %edx=1; --> mask
movl $0, %eax # %eax=0; --> result
jmp .L2
.L3:
movq %rdi, %r8 # %r8=x;
andq %rdx, %r8 # %r8=x&%rdx; -->x&mask
orq %r8, %rax # %rax=%rax | (x&%rdx); -->result |= x & mask
salq %cl, %rdx # %rdx=%rdx<<(n&0xFF); -->mask<<=(n&0xFF)
.L2:
testq %rdx, %rdx
jne .L3. # if %rdx!=0 goto L3. -->mask!=0
rep; ret
A.
%rdi, %r8 --> x
%esi, %ecx --> n
%rdx --> mask
%rax --> result
B.
result = 0;
mask = 1;
C.
mask != 0
D.
mask<<=(n&0xFF)
E.
result |= x & mask
F.
long loop(long x, int n)
{
long result = 0;
long mask;
for(mask = 1;mask != 0;mask = mask << (n&0xFF)){
result |= x & mask;
}
return result;
}
**3.61
传送指令会对条件分别求值,于是假如xp为空指针,那么这里产生对空指针读数据的操作,显然是不可以的。于是这里不能存在*xp,可以用指针来代替,最后判断出值之后,再进行读取数据,因此这里0也必须赋予一个地址,于是需要加个变量来存储0这个数字。因此答案可以是:
long cread_alt(long *xp)
{
int t=0;
int *p = xp ? xp : &t;
return *p;
}
**3.62
case MODE_A:
result = *p2;
action = *p1;
*p2 = action;
break;
case MODE_B:
result = *p1 + *p2;
*p1 = result;
break;
case MODE_C:
*p1 = 59;
result = *p2;
break;
case MODE_D:
result = *p2;
*p1 = result;
result = 27;
break;
case MODE_E:
result = 27;
break;
default:
result = 12;
**3.63
<switch_prob>:
400590: 48 83 ee 3c sub $0x3c, %rsi
# 说明下面的数都要加上60
400594: 48 83 fe 05 cmp $0x5, %rsi
400598: 77 29 ja 4005c3 <switch_prob+0x33>
# 如果大于65,跳到4005c3那一行
40059a: ff 24 f5 f8 06 40 00 jmpq *0x4006f8(,%rsi,8)
# 跳到跳转表对应的位置,假设跳转表对应数组a[x],那么分别跳到a[0x4006f8+8*(n-60)]的位置
4005a1: 48 8d 04 fd 00 00 00 lea 0x0(,%rdi,8),%rax
# 60和62会跳到这个位置
4005a8: 00
400593: c3 retq
4005aa: 48 89 f8 mov %rdi, %rax
# 63会跳到这个位置
4005ad: 48 c1 f8 03 sar $0x3, %rax
4005b1: c3 retq
4005b2: 48 89 f8 mov %rdi, %rax
# 64会跳到这个位置
4005b5: 48 c1 e0 04 shl $0x4, %rax
4005b9: 48 29 f8 sub %rdi, %rax
4005bc: 48 89 c7 mov %rax, %rdi
4005bf: 48 0f af ff imul %rdi, %rdi
# 65会跳到这个位置
4005c3: 48 8d 47 4b lea 0x4b(%rdi), %rax
# 大于65和61会跳到这个位置
4005c7: c3 retq
根据上面的分析过程可得答案如下:
long switch_prob(long x, long n){
long result = x;
switch(n):{
case 60:
case 62:
result = x * 8;
break;
case 63:
result = result >> 3;
break;
case 64:
result = (result << 4) - x;
x = result;
case 65:
x = x * x;
case 61: # 也可以去掉这行
default:
result = x + 0x4b;
}
}
***3.64
store_ele:
leaq (%rsi, %rsi, 2), %rax # %rax = 3 * j
leaq (%rsi, %rax, 4), %rax # %rax = 13 * j
leaq %rdi, %rsi # %rsi = i
salq $6, %rsi # %rsi * = 64
addq %rsi, %rdi # %rdi = 65 * i
addq %rax, %rdi # %rdi = 65 * i + 13 * j
addq %rdi, %rdx # %rdx = 65 * i + 13 * j + k
movq A(, %rdx, 8), %rax # %rax = A + 8 * (65 * i + 13 * j + k)
movq %rax, (%rcx) # *dest = A[65 * i + 13 * j + k]
movl $3640, %eax # sizeof(A) = 3640
ret
A.
&D[i][j][k] = XD + L(i * S * T + j * T + k)
B.
由A题目中的公式以及汇编至第9行第10行计算出来的可得:
S * T = 65
T = 13
S * T * R * 8 = 3640
可知:
R = 7
S = 5
T = 13
*3.65
.L6:
movq (%rdx), %rcx # t1 = A[i][j]
movq (%rax), %rsi # t2 = A[j][i]
movq %rsi, (%rdx) # A[i][j] = t2
movq %rcx, (%rax) # A[j][i] = t1
addq $8, %rdx # &A[i][j] += 8
addq $120, %rax # &A[j][i] += 120
cmpq %rdi, %rax
jne .L6 # if A[j][i] != A[M][M]
A.
从2~5行里无法区分A[i][j]和A[j][i],只能从第6和7行来看,A[i][j]每次只移动一个单位,所以每次+8的寄存器%rdx就是指的A[i][j]。
B.
因为寄存器%rdx是A[i][j],所以另一个寄存器%rax是A[j][i]。
C.
A[j][i]每次移动一行的距离,所以可得公式:8 * M = 120,显然,M=15。
*3.66
sum_col:
leaq 1(, %rdi, 4), %r8 # %r8 = 4 * n + 1
leaq (%rdi, %rdi, 2), %rax # result = 3 * n
movq %rax, %rdi # %rdi = 3 * n
testq %rax, %rax
jle .L4 # if %rax <= 0, goto L4
salq $3, %r8 # %r8 = 8 * (4 * n + 1)
leaq (%rsi, %rdx, 8), %rcx # %rcx = A[0][j]
movl $0, %eax # result = 0
movl $0, %edx # i = 0
.L3:
addq (%rcx), %rax # result = result + A[i][j]
addq $1, %rdx # i += 1
addq %r8, %rcx # 这里每次+8*(4n+1),说明每一行有4n+1个,因此NC(n)为4*n+1
cmpq %rdi, %rdx
jne .L3 # 这里说明一直循环到3*n才结束,所以可以说明一共有3n行,因此NR(n)为3*n
rep; ret
.L4:
movl $0, %eax
ret
根据上述代码中的分析,可以得出
NR(n) = 3 * n
NC(n) = 4 * n + 1
**3.67
这个的汇编翻译很简单,基本都是直接在栈上赋值了.
注意当调用一个函数时,%rsp会减去8来存一个返回地址,因此process里的24(%rsp),16(%rsp),8(%rsp)分别对应着原来的16(%rsp),8(%rsp),(%rsp)!!
A.
相对于%rsp的偏移量 存储的值
%rsp+24 z
%rsp+16 &z
%rsp+8 y
%rsp x
B.
传的是%rsp+64表示的栈地址,而不是结构体s.
C.
直接通过%rsp+偏移量的栈地址来访问的s的值.
D.
通过所传的表示栈地址的参数,来间接存储在栈上.
E.
完成eval时的栈帧图应该是:
相对于%rsp的偏移量 存储的值
%rsp+80 z
%rsp+72 x
%rsp+64 y
%rsp+32
%rsp+24 z
%rsp+16 &z
%rsp+8 y
%rsp x
在从process返回后,eval是通过直接通过访问的%rsp+偏移量来访问的结构r的元素.
F.
在涉及结构体这种无法用一个寄存器存储的参数时,不管是传入还是返回,都是直接通过在栈上的存储来进行访问的.
***3.68
首先,结构体str2类型的最长单位是long,所以按照8位对齐,str1同样,也是按照8位对齐.
汇编代码:
setVal:
movslq 8(%rsi), %rax
# 说明str2的t从第8位开始的,因为按照8位对齐,因此sizeof(array[B])小于等于8
# 因为下边的t是int类型,只占4个字节,为了不让t与array共占8个字节,所以sizeof(array[B])大于4,因此可得5<=B<=8.
addq 32(%rsi), %rax
# 说明str2的u从第32位开始的,因此t与s占了24个字节,可以将2个s放在t的一行,占满8个字节,剩下的s占据两行,因此可得7<=A<=10.
movq %rax, 184(%rdi)
# 说明str1的y从第184位开始的,因此184-8<A*B*4<=184
根据汇编代码推出的三个公式:
5<=B<=8
7<=A<=10
184-8<A*B*4<=184
可以算出唯一解为:
A=9
B=5
1
2
***3.69
<test>:
mov 0x120(%rsi), %ecx
# 这句话是访问bp的first,说明first与a一共占了288个字节
add (%rsi), %rcx
# %rcx = n
lea (%rdi, %rdi, 4), %rax
# %rax = 5 * i
lea (%rsi, %rax, 8), %rax
# %rax = &bp + 40 * i
mov 0x8(%rax), %rdx
# ap->idx = %rax + 8
# 这两句表明了&bp->a[i]的地址计算公式,即&bp+8+40i,因此可以说明,a的总大小是40
# +8说明first自己占8个字节,按照的8位对齐,因此a的第一个元素肯定是8个字节的.
movslq %ecx, %rcx
# 在这里将n进行了类型转换,int型转换成了long型,因此说明ap里的x数组一定是long型
mov %rcx, 0x10(%rax, %rdx, 8)
# 这句说明了ap->x[ap->idx]的地址计算公式是&bp + 16 + idx * 8
# +16说明了包含了first以及idx,说明idx是a的第一个元素,根据上面得出的第一个元素肯定是8个字节的结论,说明idx是long类型.
# 再因为一共占大小40,所以x数组的元素个数为(40 - 8) / 8 = 4
retq
A.
CNT = (288 - 8) / 40 = 7
B.
typedef struct {
long idx;
long x[4];
}
***3.70
注意是union类型
A.
e1.p 0
e1.y 8
e2.x 0
e2.next 8
B.
16
C.
1 proc:
2 movq 8(%rdi), %rax
3 movq (%rax), %rdx
4 movq (%rdx), %rdx
5 subq 8(%rax), %rdx
6 movq %rdx, (%rdi)
7 ret
先来看proc的C代码,等式右边中间有个减号,因此,可以去汇编里找到第5行的subq,所以2~4行就是赋值的被减数.
第3行和第4行代码分别加了两次星号,因此可以说明是((A).B)结构,根据第二行,因为是偏移量+8,取得是第二个值,e1.y不是指针,因此只能是e2.next,于是A为e2.next;同理,B说明也是指针,没有偏移量,是取得第一个值,因此只能是e1.p.所以被减数就推出来了为((up->e2.next).e1.p)
再看第5行,减数的偏移量是相对于%rax+8,上一条步骤中,%rax是(up->e2.next),取第二个值,而且汇编代码中并未加星号,因此说明不是指针,那么只能e1.y,因此减数是(up->e2.next).e1.y
最后只剩等式左边,来看第6行,偏移量为0说明取得第一个值,且从C代码中看未加星号,因此不是指针,所以只能是e2.x.
根据上述推理,可以得出C代码为:
void proc(union ele *up){
up->e2.x = *(*(up->e2.next).e1.p) - *(up->e2.next).e1.y;
}
*3.71
#include <stdio.h>
void good_echo()
{
char str[SIZE];
while(1){
char *p = fgets(str, SIZE, stdin);
if (p == NULL) {
break;
}
printf("%s",p);
}
}
1
**3.72
aframe:
pushq %rbp
movq %rsp, %rbp
subq $16, %rsp
# 将栈顶地址减小16
leaq 30(,%rdi,8), %rax
# %rax = 8 * n + 30
andq $-16, %rax
# 这里的原因跟课本中的那一处一样的道理,将后4位置0,成为最大的16的倍数.
subq %rax, %rsp
# 将栈顶地址减小%rax位
leaq 15(%rsp), %r8
andq $-16, %r8
# 这两句是保证了p的地址是16的倍数,取最小的16的倍数.
A.
s2 = s1 - ((8 * n + 30) & 0xfffffff0)
因此:
if n % 2 == 0:
s2 = s1 - (8 * n + 16)
else:
s2 = s1 - (8 * n + 24)
B.
p = (s2 + 15) & 0xfffffff0
1
C.
可以看出n在这里只有奇偶之分,s1看对16取余后的值.
首先来看使e1最小,那么e2则是最大,如果要e2最大的话,因为这里是要16倍数的最小值,因此p最小则为某个对16取余为1的值,这时e2是15,e2不可能会大于等于16了.然后使e1+e2的和也最小,则是n为偶数时,是8n+16-8n,为16,因此答案是: e1为16-e2=1,此时n为偶数,s1%16=1.
使e1最大,则e2最小,e2最小则为p恰好是16的倍数,此时e2为0.然后使e1+e2的和也最大,则是n为奇数时,是8n+24-8n,为24,因此答案是: e1为24-e2=24,此时n为奇数,s1%16=0.
D.
s2保证了能容下8 * n字节的最小的16的倍数.
p保证了自身对16对齐.
*3.73
用4个跳转就可以了.
find_range:
vxorps %xmm1, %xmm1, %xmm1
vucomiss %xmm1, %xmm0
jp .L1
ja .L2
jb .L3
je .L4
.L2:
movl $2, %eax
jmp .Done
.L3:
movl $0, %eax
jmp .Done
.L4:
movl $1, %eax
jmp .Done
.L1:
movl $3, %eax
.Done
**3.74
跟上题差不多,区别是用条件传送而不是条件分支.
find_range:
vxorps %xmm1, %xmm1, %xmm1
movq $0, %r8
movq $1, %r9
movq $2, %r10
movq $3, %rax
vucomiss %xmm1, %xmm0
cmovl %r8, %rax
cmove %r9, %rax
cmova %r10, %rax
*3.75
找规律就行了
A.
对于第n个参数,则imag部分传%xmm(2n-1),real部分传%xmm(2n-2)
B.
imag部分返回值%xmm1, real部分返回值%xmm0.



 posted on
posted on
