从如何判断浮点数是否等于0说起——浮点数的机器级表示

题目中针对的0，对于浮点类型，具体指的是0.0，自然对于指针类型就是NULL，对于整型就是0，一些常见笔试面试题中常出现，不要较真，十分欢迎提出改进意见。

本文很大程度上收到林锐博士一些文章的启发，lz也是在大学期间读过，感觉收益良多，但是当时林锐也是说了结论，lz也只是知其然，而不知其所以然，为什么要那样写？为什么要这样用？往往一深究起来就稀里糊涂了，现在有幸还是继续读书，我发现了很多问题理解的还不透彻，亡羊补牢。

比如：有int d;  int *d; bool d; double d；几个变量，经过一系列的计算之后，那么去判断这个四个变量是否等于0该怎么做？

很多菜鸟或者编程功底不扎实的就会出错，一些烂书，尤其国内的一部分大学教材，教授编程语言的书籍，比如谭xx的，都存在很多不规范的误导，甚至是错误，这样的地方简直太多了，并不是程序出了想要的正确结果，就算完事儿了。

一些类似我这样的读过几本经典书籍，看过一些经典技术手册，码过若干行的代码等等，就会说这还不简单，会类似的写出：

    void isZero(double d)
    {
        if (d >= -DBL_EPSILON && d <= DBL_EPSILON)
        {
            //d是0处理
        }
    }

    void isZero(int d)
    {
        if (0 == d)
        {
            //d是0处理
        }
    }

    void isZero(int *d)
    {
        if (NULL == d)
        {
            //d是空指针处理
        }
    }

    void isZero(bool d)
    {
        if (!d)
        {
            //d就认为是false 也就是0
        }
    }

没错，很多经典的教科书或者指南，一些技术类的讲义，都会这样教授。但是为什么要这样写？

可能一部分人就糊涂了，不知道咋回答，搞技术或者做学问不是诗词歌赋，结论经不起严谨的推敲就不能服众，不可以说，书上是这样写的，或者老师告诉我的，那样太low了。尤其是浮点数比较的问题，不只是0，类似的和其他的浮点数比较大小的问题也是一样的。

要解决这个疑惑，必须先理解计算机是如何表示和存储浮点数据的，期间参考了IEEE单双精度的规范文档，和MSDN的一些文档，以及《深入理解计算机操作系统》一书。

1、先看看双精度的伊布西龙（高等数学或者初等数学里的数学符号就是它，epsilon）的值是多少

printf("%.40lf", DBL_EPSILON);

折合为科学计数法：

2、再看一些例子

    printf("%0.100f\n", 2.7);
    printf("%0.100f\n", 0.2);

 printf("%0.100f\n", sin(3.141592653589793 / 6));

这个计算结果不是0.5，而是：

printf("%0.100f\n", 0.0000001);

打印结果是：

这样的结果在不同机器或者编译器下，有可能不同，但是能说明一个问题，浮点数的比较，不能简单的使用==，而科学的做法是依靠EPISILON，这个比较小的正数（英文单词episilon的中文解释）。

EPSILON被规定为是最小误差，换句话说就是使得EPSILON+1.0不等于1.0的最小的正数，也就是如果正数d小于EPISILON，那么d和1.0相加，计算机就认为还是等于1.0，这个EPISILON是变和不变的临界值。

官方解释：

For EPSILON, you can use the constants FLT_EPSILON, which is defined for float as 1.192092896e-07F, or DBL_EPSILON, which is defined for double as 2.2204460492503131e-016. You need to include float.h for these constants. These constants are defined as the smallest positive number x, such that x+1.0 is not equal to 1.0. Because this is a very small number, you should employ user-defined tolerance for calculations involving very large numbers.

一般可以这样写，防止出错：

    double dd = sin(3.141592653589793 / 6);
    /*if (dd == 0.5)
    {取决于不同的编译器或者机器平台……这样写，即使有时候是对的，但是就怕习惯，很容易出错。
    }*/

    if (fabs(dd - 0.5) < DBL_EPSILON)
    {
        //满足这个条件，我们就认为dd和0.5相等，否则不等
        puts("ok");//打印了ok
    }

为什么浮点数的表示是不精确的？（简单的分析，否则里面的东西太多了）

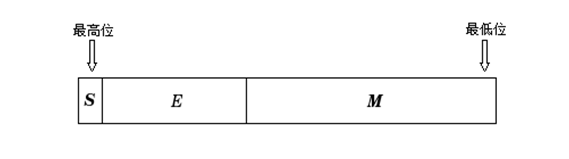
这得先说说IEEE（Institute of Electrical and Electronic Engineers ）754标准，此标准规定了标准浮点数的格式，目前，几乎所有计算机都支持该标准，这大大改善了科学应用程序的可移植性。下面看看浮点数的表示格式：n是浮点数，s是符号位，m是尾数，e是阶数，回忆高中的指数表示。

             

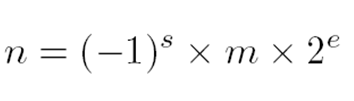
IEEE标准754规定了三种浮点数格式：单精度、双精度、扩展精度。

前两者正好对应C、C++的float、double，其中，单精度是32位，S是符号位，占1位，E是阶码，占8位，M是尾数，占23位，双精度是64位，其中S占1位，E占11位，M占52位。拿intel架构下的32位机器说话，之前在计算机存储的大小端模式解析说过处理器的两类存储方式，intel处理器是小端模式，为了简单说明，以单精度的20000.4为例子。

20000.4转换为单精度的2进制是多少？

此单精度浮点数是正数，那么尾数符号s=0，指数（阶数）e是8位，30到23位，尾数m（科学计数法的小数部分）23位长，22位到0位，共32位，如图

先看整数部分，20000先化为16进制（4e20）16，则二进制是（100 1110 0010 0000）2，一共15位。

再看小数部分，0.4化为二进制数，这里使用乘权值取整的计算方法，使用0.X循环乘2，每次取整数部分，但是我们发现，无论如何x2，都很难使得0.X为0.0，就相当于十进制的无限循环小数0.33333……一样，10进制数，无法精确的表达三分之一。也就是人们说的所谓的浮点数精度问题。因单精度浮点数的尾数规定长23位，那现在乘下去，凑够24位为止，即再续9位是（1.011001100）2

----------------------------------------------------------------------------------------------------------------

这里解释下为什么是1. ……  且 尾数需要凑够24位，而不是23位？

尾数M，单精度23位、双精度52位，但只表示小数点之后的二进制位数，也就是假定M为 “010110011...” ， 二进制是 “ . 010110011...” 。而IEEE标准规定，小数点左边还有一个隐含位，这个隐含位绝大多数情况下是1，当浮点数非常非常非常小的时候，比如小于 2^(-126) (单精度)的时候隐含位是0。这个尾数的隐含位等价于一位精度,于是M最后结果可能是"1.010110011...”或“0.010110011...”。也就是说尾数的这个隐含位占了一位精度！且尾数的隐含位这一位并不存放在内存里。

----------------------------------------------------------------------------------------------------------------

则20000.4表示为二进制 = 100 1110 0010 0000 . 0110 0110 0

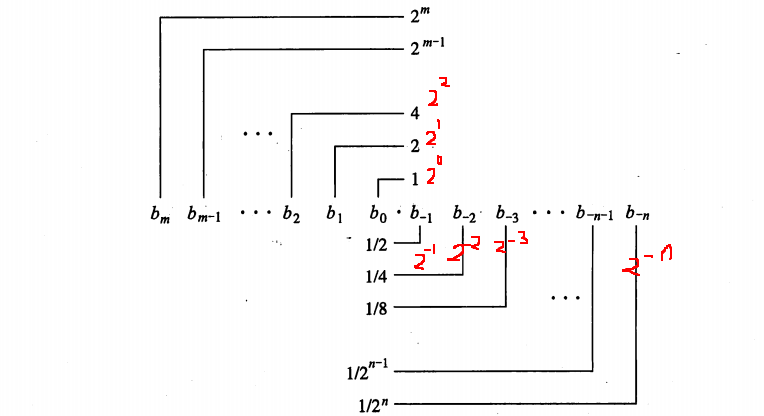
科学计数法为1.00 1110 0010 0000   0110 0110 0 x 2^14（此时尾数的隐含位是1，但是不放在内存）小数点左移了14位，单精度的阶码按IEEE标准长度是8位，可以表示范围是-128 ~ 127，又因为指数可以为负的，为了便于表示和便于计算，那么IEEE的754标准就人为的规定，指数都先加上1023（双精度的阶码位数是11位，范围是-1024~1023）或者加上127。

那么单精度的浮点，阶码的十进制就是14+127=141，141的二进制=10001101，那么阶码就是10001101，符号位是0，合并为32位就是：

0，10001101，00111000100000011001100

（1.00 1110 0010 0000   0110 0110 0尾数的小数点左边的1不存入内存）

简单的看，纵观整个过程，浮点数的表示在计算机里经常是不精确的！除非是0. ……5的情形。

因为乘不尽，且IEEE754标准规定了精度，实数由一个整数或定点数（即尾数）乘以某个基数（计算机中通常是2）的整数幂得到，这种表示方法类似于基数为10的科学记数法。

所以浮点数运算通常伴随着因为无法精确表示而进行的近似或舍入。但是这种设计的好处是可以在固定的长度上存储更大范围的数。

总之就是一句话：浮点数无法精确的表示所有二进制小数。好比：用10进制数不能精确表示某些三进制小数0.1(3)=0.33333333333……(10)，同理，用二进制小数也不能精确表示某些10进制小数。

有一个问题，为什么8位二进制的表达范围是-128到127？

必须知道：计算机里的一切数都是用补码来表示！大部分补码反码原码相关的知识在《计算机组成原理》课程都有讲授

我只说书上没有的，思考和复习了下，大概是这样的：

二进制直接表达0，有正0和负0的情况，比如原码的0000 0000和1000 0000。且计算机进行原码减法比较不爽。因为计算机里进位容易，借位比较复杂！具体怎么不爽这里不再考证。

那么最后人们决定使用补码来表达计算机里的一切数，这里不得不提一个概念——模：一个系统的计量范围，比如时钟的计量范围是12、 8位二进制数的计量范围是2^8.

对时钟：从中午12点调到下午3点，有两种方法，往前拨9个小时，或者往后拨3个小时，9+3=12，同理在计算机使用补码就是这个道理，可以使用补码代替原码，把减法化为加法。方便运算加减，且补码的0只有一种表达方式，比如四字节的补码（1000 0000 0000 0000 0000 0000 0000 0000），可以规定为-0，也可以看成0x8000 0001 - 1的结果，因为补码没有正负0，那么人为规定是后者的含义！它就是四字节负数的最小的数。那么对一字节，如下：

+127=0111 1111（原码=反码=补码）

……

+1  = 0000 0001

0    = 0000 0000

……

-126= 1111 1110（原码）= 1000 0001（反码）=1000 0010（补码）

-127= 1111 1111（原码）= 1000 0000（反码）=1000 0001（补码），显然，还差一个数，1000 0000（补码），根据前面说的，它就是一字节负数最小的数了！

就是原码-128，针对补码1000 0000求原码，记住方法，和原码求补码是一样的，都是符号位不变，取反加1，则1000 0000（补码） = 1111 1111 + 1 = 1 1000 0000（原码），精度多了一位，则舍弃，为1000 0000（原码），和补码一样。

故取值范围是1000 0000到0000 0000到0111 1111，-128到0到+127，其他位数同理，有公式曰：-2^(n-1)到+2^(n-1) - 1，其它可以套这个公式。

还有一个问题，浮点数用==比较怎么了？完全可以运行！

这个问题，其实已经呗讨论了很多年，浮点数的比较，千万不能钻牛角尖，“我就用==比较，完全能运行啊！”，我靠，没人说这句代码是错的好么？

那么到低是对还是错的，关键还是看你想要什么？！你想要的结果 和 你所做的东西反映的结果，是不是保持了一致？！明白了这个，就明白==该不该用。

其实个人认为，林锐博士 说的这是错误，感觉也不太准确，因为有钻牛角尖的会想不通。

还有一个问题，逼逼了那么多，浮点数无法精确表达实数，那为啥epsilon的大小是尼玛那样的？

#define DBL_EPSILON      2.2204460492503131E-16 
#define FLT_EPSILON     1.19209290E-07F 
#define LDBL_EPSILON     1.084202172485504E-19 

前面已经说了，数学上学的实数可以用数轴无穷尽的表示，但是计算机不行，在计算机中实数和浮点数还是不一样的，我个人理解。浮点数是属于有理数中某特定子集的数的数字表示，在计算机中用以近似表示任意某个实数。

在计算机中，整数和纯小数使用定点数表示，叫定点小数和定点正数，对混合有正数和小数的数，使用浮点数表示，所谓浮点，浮点数依靠小数点的浮动（因为有指数的存在）来动态表示实数。灵活扩大实数表达范围。但在计算过程中，难免丢失精度。

至于epsilon的大小，前面也贴出了官方定义，它就规定了，当x（假如x是双精度）落在了+- DBL_EPSILON之内，x + 1.0 = 1.0，就是这么规定的。x在此范围之内的话，都呗计算机认为是0.0 。

浮点数表达的有效位数（也就是俗称的精度）和表达范围不是一个意思

经常说什么单精度一般小数点精度是7-8位，双精度是15-16位，到低怎么来的呢？前面说了，单精度数尾数23位，加上默认的小数点前的1位1，2^(23+1) = 16777216。关键： 10^7 < 16777216 < 10^8，所以说单精度浮点数的有效位数是7-8位，这个7-8位说的是十进制下的，而我们前面说的尾数位数那是二进制下的，需要转换。

又看，双精度的尾数52位存储，2^(52+1) = 9007199254740992，那么有10^16 < 9007199254740992 < 10^17，所以双精度的有效位数是16-17位。

貌似实际编码中，大部分直接用double了，省的出错。

 

关键是要宏观的理解为什么不精确，具体怎么算倒是次要。总之应付笔试面试足够了。抛砖引玉，如有错误，欢迎指出。

 

欢迎关注

 

dashuai的博客是终身学习践行者，大厂程序员，且专注于工作经验、学习笔记的分享和日常吐槽，包括但不限于互联网行业，附带分享一些PDF电子书，资料，帮忙内推，欢迎拍砖！