并查集（不相交集合）

　　文章作者：ktyanny 文章来源：ktyanny 转载请注明，谢谢合作。

　　早上早早起来看Kruscal的MST算法，原来要用到不相交集合来实现。拿起《算法导论》看完不相交集合这章，顿然茅塞顿开，终于完成并查集的基础知识的学习。《算法导论》真是牛××

　　不相交集合有两种不同的实现，链表表示和带路径压缩的按秩合并策略。看到大家都比较喜欢用带路径压缩的按秩合并策略，那么我只认真研究了一下带路径压缩的按秩合并策略，暂时不对链表表示作讨论。

　　顾名思义，并查集的作用不就的“并”和“查”嘛。并查集的功能描述为：合并两个集合;将一元素并入另一集体;判断两个元素是否属于同一个集合。

　　通过引用两种启发式策略（按秩合并和路径压缩）就可以达到渐进意义上最快的不相交集合数据结构。 

 

1、make_set(x) 把每一个元素初始化为一个集合

建立一个新的集合，其中集合只有唯一的一个元素x

 

2、union_set(x, y) 按秩合并x，y所在的集合

  

3、find_set(x)返回x所在的集合的代表 

 

 　　

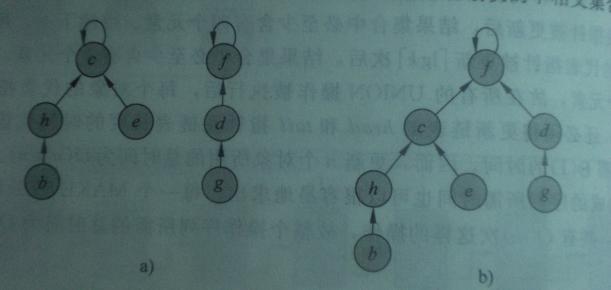
 　　在执行查找操作时，要沿着父节点指针一直找下去，直到找到树根为止。大家要注意途中的箭头。 

4、实现并查集的标准代码： 

 1 #include <stdio.h>
 2 
 3 const int MAXN = 100; /*结点数目上线*/
 4 int pa[MAXN];    /*p[x]表示x的父节点*/
 5 int rank[MAXN];    /*rank[x]是x的高度的一个上界*/
 6 
 7 void make_set(int x)
 8 {/*创建一个单元集*/
 9     pa[x] = x;
10     rank[x] = 0;
11 }
12 
13 int find_set(int x)
14 {/*带路径压缩的查找*/
15     if(x != pa[x])
16         pa[x] = find_set(p[x]);
17     return pa[x];
18 }
19 
20 /*按秩合并x，y所在的集合*/
21 void union_set(int x, int y)
22 {
23     x = find_set(x);
24     y = find_set(y);
25     if(rank[x] > rank[y])/*让rank比较高的作为父结点*/
26         pa[y] = x;
27     else 
28     {
29         pa[x] = y;
30         if(rank[x] == rank[y])
31             rank[y]++;
32     }
33 }

 

 相关练习：

POJ 1611 The Suspects （并查集）   

POJ  2524 Ubiquitous Religions (并查集)