【poj 1182】食物链(图论--带权并查集)
题意:有3种动物A、B、C,形成一个“A吃B, B吃C,C吃A ”的食物链。有一个人对N只这3类的动物有M种说法:第一种说法是"1 X Y",表示X和Y是同类。;第二种说法是"2 X Y",表示X吃Y。假设输入为(d,X,Y)。可知,当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
1) 当前的话与前面的某些真的话冲突,就是假话;
2) 当前的话中X或Y比N大,就是假话;
3) 当前的话表示X吃X,就是假话。
要求输出假话的总数。
解法:带权并查集。同【bzoj 1202】[HNOI2005] 狡猾的商人(图论--带权并查集+前缀和)类似,判断假话的条件一就是要与之前得到的结果冲突。所以推断出用并查集的原因:绝对不是因为有3“种”动物,而是因为这个“之前有结果就判断,没有结果就存储”的操作。
于是由于已经知道要用并查集,就需要推出树上结点的关系,使f[x]表示动物x与其所在联盟的根节点R的关系(x→R)。再通过枚举的方法,列举出所有情况,得出规律。再应用到具体的函数等操作中。
QUESTION!!!(这里理应大写加粗~) OMG!!!∑(゚Д゚ノ)ノ我突然间发现若用“方块图”,我下面的所有推导都显得无比无比的复杂啊!直接转换x→y(定义x下y上)的关系为:x到y的距离 或 x上面方块的个数,所有的都可以一步写出来呀!有神牛告诉我带权并查集都是可以这样理解的吗?!!!!所有的找父亲结点并更新自己的find(x)函数那里,f[x]都是f[x]+f[fx]吗。。。
推导过程如下:如图1所示,设x,y分别是R的子结点;如图2所示,x→R表示x吃R,相应数字。0为x,R同类,1为x吃R,2为R吃x;具体对应情况枚举如图3所示。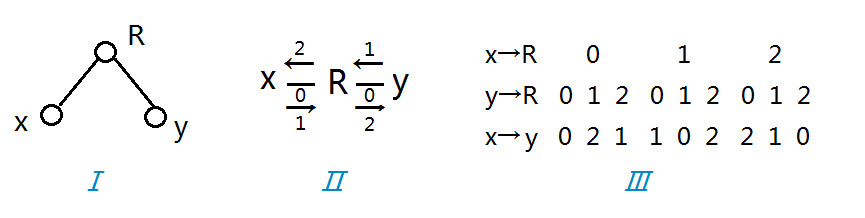
于是据图3找规律,相加不行便相减,发现(第一行数-第二行数+3)%3=第三行数,即(f[x]-f[y]+3)%3=d-1。(d为输入中x,y的关系种类)
因此,根据这一条树上的规律,我们就可以把它应用到所有函数中了。具体请见代码——

1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 using namespace std; 6 7 const int N=50010,M=100010; 8 int fa[N],f[N]; 9 int n,m; 10 11 int ffind(int x) 12 { 13 if (fa[x]!=x) 14 { 15 int fx=fa[x]; 16 fa[x]=ffind(fx); 17 /*推导: 18 f[x]=(f[x]-f[fa[x]]+3)%3; 19 =(f[x]-((3-f[fx])%3)+3)%3; 20 */ 21 f[x]=(f[x]+f[fx])%3; 22 } 23 return fa[x]; 24 } 25 int main() 26 { 27 scanf("%d%d",&n,&m); 28 int cnt=0; 29 for (int i=1;i<=n;i++) fa[i]=i,f[i]=0; 30 for (int i=1;i<=m;i++) 31 { 32 int d,x,y; 33 scanf("%d%d%d",&d,&x,&y); 34 if (x>n||y>n||(d==2&&x==y)) {cnt++;continue;} 35 d--;// 36 int fx=ffind(x),fy=ffind(y); 37 if (fx!=fy) 38 { 39 fa[fx]=fy; 40 /*推导: 41 int t=(3-f[x])%3;//fx->x 42 int tt=(3-d)%3;//y->x 43 int w=(t-tt+3)%3;//fx->y 44 int ww=(3-f[y])%3;//fy->y 45 f[fx]=(w-ww+3)%3;//fx->fy 46 */ 47 f[fx]=(f[y]-f[x]+d+3)%3; 48 } 49 else if ((f[x]-f[y]+3)%3!=d) cnt++; 50 } 51 printf("%d\n",cnt); 52 return 0; 53 }
--------------------------------------------------------------------------------------------------------------------------------
另外啊~我学习了一下好友的做法:x->y间的边权直接看成距离,1为x吃y,0为同类。这样一个食物链的x,y,z的关系都可直接推出!!○| ̄|_ orz~
还有,合并父亲时,可以让y变为fx的父亲,而不是fy变为fx的父亲,这样虽然增大了树的深度,但影响不大,重要的是可以节省一些代码。




