面试题7：字符串的全排列

题目描述

输入一个字符串，打印出该字符串中字符的所有排列。例如，输入字符串”abc”，则输出由字符’a’，’b’，’c’所能排列出来的所有字符串”abc”，”acb”，”bac”，”bca”，”cab”和”cba”。

方法一：递归实现

基本思想：

从字符串中选出一个字符作为排列的第一个字符，然后对剩余的字符进行全排列。如此递归下去，从而得到所有字符的全排列。

核心思想就是从第一个数字起每个数分别与它后面的数字交换

//全排列的递归实现  
#include <iostream>
#include <string.h>  

using namespace std;

void Swap(char *a, char *b)  
{  
    char t = *a;  
    *a = *b;  
    *b = t;  
}  
//k表示当前选取到第几个数,m表示共有多少数.  
void AllRange(char *pszStr, int k, int m)  
{  
    if (k == m)  
    {  
        static int s_i = 1;  
        cout << "第 " << s_i++ << " 个排列 " << pszStr << endl;  
    }  
    else  
    {  
        for (int i = k; i <= m; i++) //第i个数分别与它后面的数字交换就能得到新的排列  
        {  
            Swap(pszStr + k, pszStr + i);  
            AllRange(pszStr, k + 1, m);  
            Swap(pszStr + k, pszStr + i);  
        }  
    }  
}  
void Foo(char *pszStr)  
{  
    AllRange(pszStr, 0, strlen(pszStr) - 1);  
}  
int main()  
{  
    cout << "全排列的递归实现" << endl;;  
    char szTextStr[] = "abc";  
    cout << szTextStr <<"的全排列如下:" << endl;
   
    Foo(szTextStr); 
    system("pause");
    return 0;  
}  

运行结果如下：

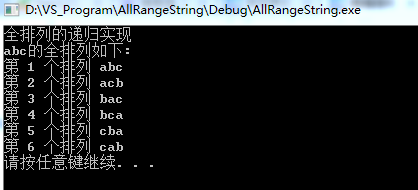
注意：这样的方法没有考虑到重复数字，如abb将会输出：

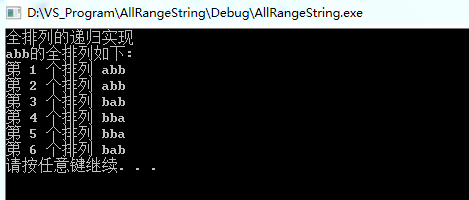
 看到这样的输出结果是绝对不符合要求的，因此对于有重复字符的字符串要做出修改。

方法二：去掉重复字符的全排列的递归实现

由于全排列就是从第一个数字起每个数分别与它后面的数字交换。

我们先尝试加个这样的判断：如果一个数与后面的数字相同，那么这两个数就不交换了。

如abb，第一个数与后面交换得bab、bba；然后abb中第二数就不用与第三个数交换了，但对bab，它第二个数与第三个数是不相同的，交换之后得到bba。与由abb中第一个数与第三个数交换所得的bba重复了。所以这个方法不行。

换种思维，对abb，第一个数a与第二个数b交换得到bab，然后考虑第一个数a与第三个数b交换，此时由于第三个数等于第二个数，所以第一个数不再与第三个数交换。再考虑bab，它的第二个数与第三个数交换可以得到解决bba。此时全排列生成完毕。

这样我们也得到了在全排列中去掉重复的规则——去重的全排列就是从第一个数字起每个数分别与它后面非重复出现的数字交换。用编程的话描述就是第i个数与第j个数交换时，要求[i,j)中没有与第j个数相等的数。

//全排列的递归实现  
#include <iostream>
#include <string.h>  

using namespace std;

void Swap(char *a, char *b)  
{  
    char t = *a;  
    *a = *b;  
    *b = t;  
}  

//在pszStr数组中，[nBegin,nEnd)中是否有数字与下标为nEnd的数字相等  
bool IsSwap(char *pszStr, int nBegin, int nEnd)  
{  
    for (int i = nBegin; i < nEnd; i++)  
        if (pszStr[i] == pszStr[nEnd])  
            return false;  
    return true;  
} 



//k表示当前选取到第几个数,m表示共有多少数.  
void AllRange(char *pszStr, int k, int m)  
{  
    if (k == m)  
    {  
        static int s_i = 1;  
        cout << "第 " << s_i++ << " 个排列 " << pszStr << endl;  
    }  
    else  
    {  
        for (int i = k; i <= m; i++) //第i个数分别与它后面的数字交换就能得到新的排列  
        {  
            if (IsSwap(pszStr, k, i))  
            {  
                Swap(pszStr + k, pszStr + i);  
                AllRange(pszStr, k + 1, m);  
                Swap(pszStr + k, pszStr + i);  
            }  
        }  
    }  
}  

void Foo(char *pszStr)  
{  
    AllRange(pszStr, 0, strlen(pszStr) - 1);  
}

int main()  
{  
    cout << "全排列的递归实现" << endl;;  
    char szTextStr[] = "abb";  
    cout << szTextStr <<"的全排列如下:" << endl;
   
    Foo(szTextStr); 
    system("pause");
    return 0;  
}  

运行结果如下：

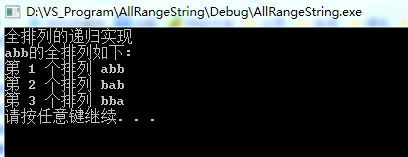
方法三：非递归实现字符串的全排列

要考虑全排列的非递归实现，先来考虑如何计算字符串的下一个排列。如"1234"的下一个排列就是"1243"。只要对字符串反复求出下一个排列，全排列的也就迎刃而解了。

如何计算字符串的下一个排列了？来考虑"926520"这个字符串，我们从后向前找第一双相邻的递增数字，"20"、"52"都是非递增的，"26 "即满足要求，称前一个数字2为替换数，替换数的下标称为替换点，再从后面找一个比替换数大的最小数（这个数必然存在），0、2都不行，5可以，将5和2交换得到"956220"，然后再将替换点后的字符串"6220"颠倒即得到"950226"。

对于像"4321"这种已经是最“大”的排列，采用STL中的处理方法，将字符串整个颠倒得到最“小”的排列"1234"并返回false。

这样，只要一个循环再加上计算字符串下一个排列的函数就可以轻松的实现非递归的全排列算法。按上面思路并参考STL中的实现源码，不难写成一份质量较高的代码。值得注意的是在循环前要对字符串排序下，可以自己写快速排序的代码，也可以直接使用VC库中的快速排序函数。

#include <iostream>  
#include <string.h>  

using namespace std;
void Swap(char *a, char *b)  
{  
    char t = *a;  
    *a = *b;  
    *b = t;  
}  
//反转区间  
void Reverse(char *a, char *b)  
{  
    while (a < b)  
        Swap(a++, b--);  
}  
//下一个排列  
bool Next_permutation(char a[])  
{  
    char *pEnd = a + strlen(a);  
    if (a == pEnd)  
        return false;  
    char *p, *q, *pFind;  
    pEnd--;  
    p = pEnd;  
    while (p != a)  
    {  
        q = p;  
        --p;  
        if (*p < *q) //找降序的相邻2数,前一个数即替换数  
        {  
            //从后向前找比替换点大的第一个数  
            pFind = pEnd;  
            while (*pFind <= *p)  
                --pFind;  
            //替换  
            Swap(pFind, p);  
            //替换点后的数全部反转  
            Reverse(q, pEnd);  
            return true;  
        }  
    }  
    Reverse(p, pEnd);//如果没有下一个排列,全部反转后返回true  
    return false;  
}  
int QsortCmp(const void *pa, const void *pb)  
{  
    return *(char*)pa - *(char*)pb;  
} 

int main()  
{  
    cout << "全排列的非递归实现" << endl;    
 
    char szTextStr[] = "abb";  
    cout << szTextStr <<"的全排列如下:" << endl; 
    //加上排序  
    qsort(szTextStr, strlen(szTextStr), sizeof(szTextStr[0]), QsortCmp);  
    int i = 1;  
    do
    {  
        cout << "第 " << i++ << " 个排列 " << szTextStr << endl;    
    }while (Next_permutation(szTextStr)); 

    system("pause");
    return 0;  
}  

 运行结果：

 

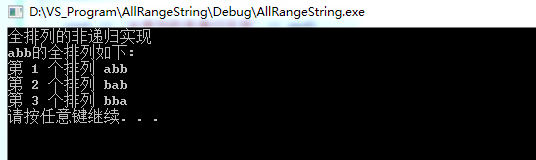
 至此我们已经运用了递归与非递归的方法解决了全排列问题，总结一下就是：

 1．全排列就是从第一个数字起每个数分别与它后面的数字交换。

 2．去重的全排列就是从第一个数字起每个数分别与它后面非重复出现的数字交换。

 3．全排列的非递归就是由后向前找替换数和替换点，然后由后向前找第一个比替换数大的数与替换数交换，最后颠倒替换点后的所有数据。

 

 援引：http://blog.csdn.net/morewindows/article/details/7370155