K中心点算法之PAM
对比kmeans:k-means是每次选簇的均值作为新的中心,迭代直到簇中对象分布不再变化。其缺点是对于离群点是敏感的,因为一个具有很大极端值的对象会扭曲数据分布。那么我们可以考虑新的簇中心不选择均值而是选择簇内的某个对象,只要使总的代价降低就可以。kmedoids算法比kmenas对于噪声和孤立点更鲁棒,因为它最小化相异点对的和(minimizes a sum of pairwise dissimilarities )而不是欧式距离的平方和(sum of squared Euclidean distances.)。一个中心点(medoid)可以这么定义:簇中某点的平均差异性在这一簇中所有点中最小。
1. 初始化:随机挑选n个点中的k个点作为中心点。
2. 将其余的点根据距离划分至这k个类别中。
3. 当损失值减少时:
1)对于每个中心点m,对于每个非中心点o:
i)交换m和o,重新计算损失(损失值的大小为:所有点到中心点的距离和)
ii)如果总的损失增加则不进行交换
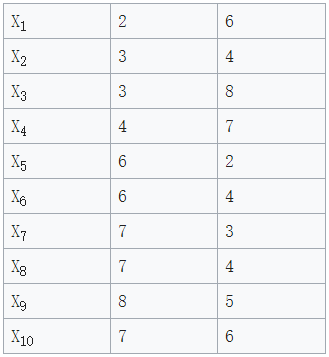
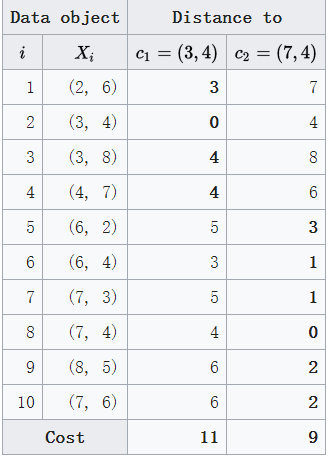
1. 随机挑选k=2个中心点:c1=(3,4) , c2=(7,4).那么将所有点到这两点的距离计算出来(图2),可以看到黑体为到两个中心点距离较小的距离值。那么根据图2,我们可以对所有数据点进行归类:
Cluster1 = {(3,4)(2,6)(3,8)(4,7)}
Cluster2 = {(7,4)(6,2)(6,4)(7,3)(8,5)(7,6)}
很容易算出此时的损失值cost为:20
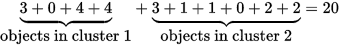
2. 挑选一个非中心点O’,让我们假定挑选的为X7 ,即O‘=(7,3)。那么此时这两个中心点暂时变成了c1(3,4) and O′(7,3),那么我们要计算一下这一替换措施所带来的损失cost:

图3 图4
正如图3和图4所见,此时的cost(很好计算,黑体数值的和)变成了: total cost = 3+4+4+2+2+1+3+3 = 22
此时的cost为22,比之前的cost=20要大,所以这次替换的损失变大啦,我们最终不进行这次替换。
这仅仅是X7 替代了c2点,我们应该计算除了c1和c2点外的所有点外分别替代c1和c2,将这些替换后的损失都计算出来,看看有没有比20小的损失,如果有那么我们就将这个最小损失对应的中心点对作为新的中心点对。至此才完成了一次迭代。重复迭代直至收敛。
#!/usr/bin/env python3 # -*- coding: utf-8 -*- """ Created on Sun Oct 22 20:31:32 2017 @author: LPS """ import numpy as np import pandas as pd import copy df = np.loadtxt('waveform.txt',delimiter=',') # 载入waveform数据集,22列,最后一列为标签0,1,2 s= np.array(df) print(s.shape) print(s[0:10]) data0 = s[s[:,s.shape[1]-1]==0][:100] # 取标签为0的前100个样本 data1 = s[s[:,s.shape[1]-1]==1][:100] # 取标签为1的前100个样本 data2 = s[s[:,s.shape[1]-1]==2][:100] # 取标签为2的前100个样本 data = np.array([data0,data1,data2]) data = data.reshape(-1,22) def dis(data_a, data_b): return np.sqrt(np.sum(np.square(data_a - data_b), axis=1)) # 返回欧氏距离 def kmeans_wave(n=10, k=3, data=data): data_new = copy.deepcopy(data) # 前21列存放数据,不可变。最后1列即第22列存放标签,标签列随着每次迭代而更新。 data_now = copy.deepcopy(data) # data_now用于存放中间过程的数据 center_point = np.random.choice(300,3,replace=False) center = data_new[center_point,:20] # 随机形成的3个中心,维度为(3,21) distance = [[] for i in range(k)] distance_now = [[] for i in range(k)] # distance_now用于存放中间过程的距离 lost = np.ones([300,k])*float('inf') # 初始lost为维度为(300,3)的无穷大 for j in range(k): # 首先完成第一次划分,即第一次根据距离划分所有点到三个类别中 distance[j] = np.sqrt(np.sum(np.square(data_new[:,:20] - np.array(center[j])), axis=1)) data_new[:, 21] = np.argmin(np.array(distance), axis=0) # data_new 的最后一列,即标签列随之改变,变为距离某中心点最近的标签,例如与第0个中心点最近,则为0 for i in range(n): # 假设迭代n次 for m in range(k): # 每一次都要分别替换k=3个中心点,所以循环k次。这层循环结束即算出利用所有点分别替代3个中心点后产生的900个lost值 for l in range(300): # 替换某个中心点时都要利用全部点进行替换,所以循环300次。这层循环结束即算出利用所有点分别替换1个中心点后产生的300个lost值 center_now = copy.deepcopy(center) # center_now用于存放中间过程的中心点 center_now[m] = data_now[l,:20] # 用第l个点替换第m个中心点 for j in range(k): # 计算暂时替换1个中心点后的距离值 distance_now[j] = np.sqrt(np.sum(np.square(data_now[:,:20] - np.array(center_now[j])), axis=1)) data_now[:, 21] = np.argmin(np.array(distance), axis=0) # data_now的标签列更新,注意data_now时中间过程,所以这里不能选择更新data_new的标签列 lost[l, m] = (dis(data_now[:, :20], center_now[data_now[:, 21].astype(int)]) \ - dis(data_now[:, :20], center[data_new[:, 21].astype(int)])).sum() # 这里很好理解lost的维度为什么为300*3了。lost[l,m]的值代表用第l个点替换第m个中心点的损失值 if np.min(lost) < 0: # lost意味替换代价,选择代价最小的来完成替换 index = np.where(np.min(lost) == lost) # 即找到min(lost)对应的替换组合 index_l = index[0][0] # index_l指将要替代某个中心点的候选点 index_m = index[1][0] # index_m指将要被替代的某个中心点,即用index_l来替代index_m center[index_m] = data_now[index_l,:20] #更新聚类中心 for j in range(k): distance[j] = np.sqrt(np.sum(np.square(data_now[:, :20] - np.array(center[j])), axis=1)) data_new[:, 21] = np.argmin(np.array(distance), axis=0) # 更新参考矩阵,至此data_new的标签列得以更新,即完成了一次迭代 return data_new # 最后返回data_new,其最后一列即为最终聚好的标签 if __name__ == '__main__': data_new = kmeans_wave(10,3,data) print(data_new.shape) print(np.mean(data[:,21] == data_new[:,21])) # 验证划分准确度
附:利用上面实现的代码对图片聚类。结果发现和kmeans相比实在是太慢了。就拿500*500的三通道jpg来说,有500*500=250000个像素值,即这个图像的数据集维度为(250000,3)。而上文我们实现的数据集维度仅仅为(300, 3)。这意味每次迭代都要循环250000*3次。所以我只好截选了一张小图来测试。。代码与结果如下:
 pam for image
pam for image 

图1.从1200*800图中截取的70*70的图片 图2. 迭代20次k=3的结果
其实这个结果意义不大,只是作为测试。因为像素分布太集中,可以选择其他分布较散的图像,此外改进pam算法来实现更高效的聚类。


