支持向量机（三）非线性支持向量机与核函数

支持向量机（一）线性可分支持向量机

支持向量机（二）线性支持向量机

支持向量机（三）非线性支持向量机与核函数

支持向量机（四）SMO算法

目录

• 一、核技巧
  • 1.非线性分类问题
  • 2.核函数的定义
  • 3.核技巧在支持向量机的应用
• 二、正定核
  • 1.定义映射，构成向量空间 S
• 三、常用核函数
  • 1.线性核函数
  • 2.多项式核函数
  • 3.高斯核函数
  • 4.拉普拉斯核函数
  • 5.Sigmoid核函数
  • 6.字符串核函数
• 四、非线性支持向量机
  • 1.非线性支持向量机学习算法
• 五、总结

一、核技巧

1.非线性分类问题

如图 \(7.7\)，无法用直线（线性模型）将正实例点 “●”、负实例点 “×” 正确分开，但可用一条椭圆曲线（非线性模型）将其分开。

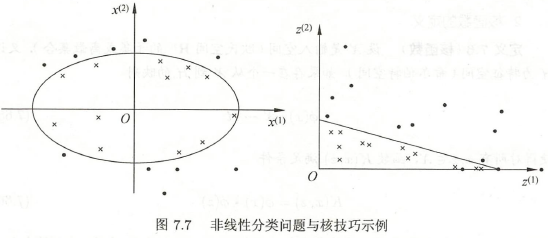
非线性问题不好求解，可将非线性问题变换为线性问题，如图 \(7.7\)，将左图中的椭圆变为右图中的直线。

设原空间为 \(\chi \subset \pmb{R^2},x=(x^{(1)}, x^{(2)})^T \in \chi\)，新空间为 \(\mathcal{Z} \subset \pmb{R^2}, z=(z^{(1)}, z^{(2)})^T \in \mathcal{Z}\)，定义从原空间到新空间的变化：

\[z=\phi(x)=((x^{(1)})^2, (x^{(2)})^2)^T \]

原空间的椭圆

\[\omega_1(x^{(1)})^2 + \omega_2(x^{(2)})^2 + b = 0 \]

变为新空间中的直线

\[\omega_1 z^{(1)} + \omega_2 z^{(2)} + b = 0 \]

这样，非线性问题变换为线性问题。

核技巧：通过一个非线性变换 将输入空间（欧式空间 \(\pmb{R^2}\) 或离散集合）对应于一个特征空间（希尔伯特空间 \(\mathcal{H}\)），使输入空间 \(\pmb{R^n}\) 的超曲面模型对应于特征空间 \(\mathcal{H}\) 中的超平面模型（支持向量机）。

2.核函数的定义

定义： 设 \(\chi\) 是输入空间，\(\mathcal{H}\) 为特征空间，如果存在从 \(\chi\) 到 \(\mathcal{H}\) 的映射

\[\tag{1} \phi(x): \chi \to \mathcal{H} \]

使得对所有 \(x,z \in \chi\)，函数 \(K(x,z)\) 满足条件

\[\tag{2} K(x,z) = \phi(x) \cdot \phi(z) \]

则称 \(K(x,z)\) 为核函数，\(\phi(x)\) 为映射函数。

对于给定的核函数 \(K(x,z)\)，特征空间 \(\mathcal{H}\) 和映射函数 \(\phi\) 取法不唯一，可以取不同的特征空间，即使同一特征空间也可以取不同的映射。

实例 \(1\)： 输入空间 \(\pmb{R^2}\)，核函数 \(K(x,z)=(x \cdot z)^2\)，找出其相关的特征空间 \(\mathcal{H}\) 和映射 \(\phi(x)\)。

解： 取特征空间 \(\mathcal{H}=\pmb{R^3}\)，记 \(x=(x^{(1)},x^{(2)})^T\)，\(z=(z^{(1)},z^{(1)})^T\)，由于

\[\begin{aligned} (x \cdot z)^2 & = (x^{(1)} z^{(1)} + x^{(2)} z^{(2)})^2 \\ & = (x^{(1)} z^{(1)})^2 + 2 x^{(1)} z^{(1)} x^{(2)} z^{(2)} + (x^{(2)} z^{(2)})^2 \end{aligned} \]

所以可以取映射

\[\phi(x) = ((x^{(1)})^2, \sqrt{2} x^{(1)} x^{(2)}, (x^{(2)})^2)^T \]

容易验证 \(\phi(x) \cdot \phi(z) = (x \cdot z)^2 = K(x,z)\)。

仍取 \(\mathcal{H}=\pmb{R^3}\) 以及

\[\phi(x) = \frac{1}{\sqrt{2}} ((x^{(1)})^2 - (x^{(2)})^2, 2 x^{(1)} x^{(2)}, (x^{(1)})^2+(x^{(2)})^2)^T \]

同样有 \(\phi(x) \cdot \phi(z) = (x \cdot z)^2 = K(x,z)\)。

还可以取 \(\mathcal{H}=\pmb{R^4}\) 和

\[\phi(x) = ((x^{(1)})^2, x^{(1)} x^{(2)}, x^{(1)} x^{(2)}, (x^{(2)})^2)^T \]

3.核技巧在支持向量机的应用

线性支持向量机的对偶问题中，目标函数、决策函数都只涉及输入实例与实例之间的内积。

将对偶问题的目标函数中的内积 \(x_i \cdot x_j\) 用核函数 \(K(x_i,x_j)=\phi(x_i) \cdot \phi(x_j)\) 来代替。此时对偶问题的目标函数为

\[W(\alpha) = \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j y_i y_j K(x_i,x_j) - \sum_{i=1}^{N} \alpha_i \]

分类决策函数为

\[\begin{aligned} f(x) & =sign(\sum_{i=1}^{N_s} \alpha_i^* y_i \phi(x_i) \phi(x) + b^*) \\ & = sign(\sum_{i=1}^{N_s} \alpha_i^* y_i K(x_i,x) + b^*) \end{aligned} \]

这等价于经过映射函数 \(\phi\) 将输入空间中的内积 \(x_i \cdot x_j\) 变换为特征空间中的内积 \(\phi(x_i) \cdot \phi(x_j)\)，在新的特征空间里学习线性支持向量机。

当映射函数是非线性时，学习到含有核函数的支持向量机是非线性支持向量机。学习是隐式地在特征空间进行的，不需要显示地定义特征空间和映射函数。

二、正定核

对称函数 \(K(x,z)\) 成为核函数（通常指正定核函数）的充要条件：设 \(K(x,z)\) 是定义在 \(\chi \times \chi\) 上的对称函数，即 \(K(x,z)=K(z,x)\)，对任意的 \(x_1,x_2,...,x_m \in \chi\)，\(K(x,z)\) 对应的 \(Gram\) 矩阵是半正定的。

希尔伯特空间：是一个完备的，可能是无限维的，被赋予内积的线性空间（线性空间亦称向量空间）。

完备：指的是对极限计算是封闭的，即计算结果还是属于线性空间。

线性空间：指的是对加法、数乘计算是封闭的，即计算结果还是属于线性空间。

希尔伯特空间是函数空间，它的每一个元素都可以看作是函数。

构成希尔伯特空间的步骤：定义映射函数 \(\phi\) 并构成向量空间 \(S\)；然后在 \(S\) 上定义内积构成内积空间；最后将 \(S\) 完备化构成希尔伯特空间。

1.定义映射，构成向量空间 S

定义映射

\[\phi : x \to K(\ \cdot \ , x) \]

根据这一映射，对任意的 \(x_i \in \chi\)，\(\alpha_i \in \pmb{R}\)，\(i=1,2,...,m\)，定义线性组合

\[f(\cdot) = \sum_{i=1}^{N} \alpha_i K(\ \cdot \ , x_i) \]

三、常用核函数

1.线性核函数

\[K(x,z) = x \cdot z \]

线性核函数对应的是线性可分支持向量机。

2.多项式核函数

\[K(x,z) = (x \cdot z + 1)^P \]

对应的支持向量机是一个 \(p\) 次多项式分类器。此时的分类决策函数为

\[f(x) = sign(\sum_{i=1}^{N_s} \alpha_i^* y_i (x_i \cdot x + 1)^p + b^*) \]

3.高斯核函数

\[K(x,z) = exp(- \frac{||x-z||^2}{2\sigma^2}), \ \ \ \ \sigma>0 \]

对应的支持向量机是高斯径向基函数分类器。此时分类决策树函数为

\[f(x) = sign(\sum_{i=1}^{N_s} \alpha_i^* y_i exp(- \frac{||x-z||^2}{2\sigma^2}) + b^*) \]

4.拉普拉斯核函数

\[K(x,z) = exp(- \frac{||x-z||^2}{\sigma}), \ \ \ \ \sigma>0 \]

5.Sigmoid核函数

\[K(x,z) = tanh(\beta x \cdot z + \theta),\ \ \ \ \beta>0,\theta<0 \]

6.字符串核函数

核函数不仅定义在欧式空间，还可定义在离散数据的集合上。

比如，字符串核是定义在字符串集合上的核函数。字符串核函数在文本分类、信息检索、生物信息等方面都有应用。

四、非线性支持向量机

利用核技巧，将线性分类的学习方法应用到非线性分类问题中。

将线性支持向量机扩展到非线性支持向量机，只需将线性支持向量机对偶形式中的内积换成核函数。

从非线性分类训练集，通过核函数与软间隔最大化，或凸二次规划 \((3)\)~\((5)\)，学习得到的分类决策函数

\[\tag{3} f(x) = sign(\sum_{i=1}^{N} \alpha_i^* y_i K(x, x_i) + b^*) \]

称为非线性支持向量机，\(K(x,z)\) 是正定核函数。

1.非线性支持向量机学习算法

输入：训练集 \(T=\{(x_1,y_1), (x_2,y_2),...,(x_N,y_N)\}\)，其中 \(x_i \in \chi = \pmb{R^n}\)，\(y_i \in \mathcal{Y}=\{-1,1\}\)，\(i=1,2,...,N\)

输出：分类决策树

① 选取核函数 \(K(x,z)\) 和参数 \(C\)，构造并求解最优化问题

\[\begin{align} \tag{3} \underset{\alpha}{min} \ \ \ \ & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j y_i y_j K(x_i, x_j) - \sum_{i=1}^{N} \alpha_i \\ \tag{4} s.t. \ \ \ \ & \sum_{i=1}^{N} \alpha_i y_i=0 \\ \tag{5} & 0 \le \alpha_i \le C, \ \ \ \ i=1,2,...,N \end{align} \]

求最优解 \(\alpha^* = (\alpha_1^*, \alpha_2^*,...,\alpha_N^*)^T\)。

② 选择 \(\alpha^*\) 的一个正分量 \(0< \alpha_j^* < C\)，计算

\[b^* = y_j - \sum_{i=1}^{N} \alpha_i^* y_i K(x_i,x_j) \]

③ 构造决策函数：

\[f(x) = sign(\sum_{i=1}^{N} \alpha_i^* y_i K(x,x_i) + b^*) \]

当 \(K(x,z)\) 是正定核函数时， \((3)\)~\((5)\) 是凸二次规划问题，解存在。

五、总结

• 对于输入空间中的非线性分类问题，通过非线性变换转化为高维特征空间中的线性分类问题。然后在高维特征空间中学习线性支持向量机。

• 由于在线性支持向量机学习的对偶问题里，目标函数和分类决策函数都只涉及实例与实例之间的内积，所以不需要显式地指定非线性变换，而是用核函数来替换当中的内积。

• 核函数表示，通过一个非线性转换后的两个实例间的内积。

  具体地，\(K(x,z)\) 是一个核函数，或正定核，意味着存在一个从输入空间 \(\chi\) 到特征空间 \(\mathcal{H}\) 的映射 \(\phi(x)\)：\(\chi \to \mathcal{H}\)，对任意的 \(x,z \in \chi\)，有

  \[K(x,z) = \phi(x) \cdot \phi(z) \]

• 对称函数 \(K(x,z)\) 为正定核的充要条件：里面任何点的集合形成的 \(Gram\) 矩阵是半正定的。即对任意 \(x_i \in \chi\)，\(i=1,2,...,m\)，对任意正整数 \(m\)，对称函数 \(K(x,z)\) 对应的 \(Gram\) 矩阵是半正定的。所以在线性支持向量机学习的对偶问题中，用核函数 \(K(x,z)\)替代内积，求得的就是非线性支持向量机

  \[f(x) = sign(\sum_{i=1}^{N} \alpha_i^* y_i K(x,x_i) + b^*) \]