似然函数的概念
(源自:维基百科)
在数理统计学中,似然函数是一种关于统计模型中的参数的函数,表示模型参数中的似然性。
似然函数在统计推断中有重大作用,如在最大似然估计和费雪信息之中的应用等等。“似然性”与“或然性”或“概率”意思相近,都是指某种事件发生的可能性,但是在统计学中,“似然性”和“或然性”或“概率”又有明确的区分。
概率 用于在已知一些参数的情况下,预测接下来的观测所得到的结果,而
似然性 则是用于在已知某些观测所得到的结果时,对有关事物的性质的参数进行估计。
在这种意义上,似然函数可以理解为条件概率的逆反。
在已知某个参数B时,事件A会发生的概率写作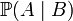 。
。
利用贝叶斯定理,
因此,我们可以反过来构造表示似然性的方法:已知有事件A发生,运用似然函数 ,我们估计参数B的可能性。
,我们估计参数B的可能性。
形式上,似然函数也是一种条件概率函数,但我们关注的变量改变了:
注意到这里并不要求似然函数满足归一性: 。一个似然函数乘以一个正的常数之后仍然是似然函数。对所有α > 0,都可以有似然函数:
。一个似然函数乘以一个正的常数之后仍然是似然函数。对所有α > 0,都可以有似然函数:
![]()
例子:
考虑投掷一枚硬币的实验。通常来说,已知投出的硬币正面朝上和反面朝上的概率各自是pH = 0.5,便可以知道投掷若干次后出现各种结果的可能性。比如说,投两次都是正面朝上的概率是0.25。用条件概率表示,就是:
其中H表示正面朝上。
在统计学中,我们关心的是在已知一系列投掷的结果时,关于硬币投掷时正面朝上的可能性的信息。我们可以建立一个统计模型:假设硬币投出时会有pH 的概率正面朝上,而有1 − pH 的概率反面朝上。这时,条件概率可以改写成似然函数:
也就是说,对于取定的似然函数,在观测到两次投掷都是正面朝上时,pH = 0.5 的似然性是0.25(这并不表示当观测到两次正面朝上时pH = 0.5 的概率是0.25)。
如果考虑pH = 0.6,那么似然函数的值也会改变。
注意到似然函数的值变大了。这说明,如果参数pH 的取值变成0.6的话,结果观测到连续两次正面朝上的概率要比假设pH = 0.5时更大。也就是说,参数pH 取成0.6 要比取成0.5 更有说服力,更为“合理”。总之,似然函数的重要性不是它的具体取值,而是当参数变化时函数到底变小还是变大。对同一个似然函数,如果存在一个参数值,使得它的函数值达到最大的话,那么这个值就是最为“合理”的参数值。
在这个例子中,似然函数实际上等于:
 , 其中
, 其中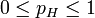 。
。
如果取pH = 1,那么似然函数达到最大值1。也就是说,当连续观测到两次正面朝上时,假设硬币投掷时正面朝上的概率为1是最合理的。
类似地,如果观测到的是三次投掷硬币,头两次正面朝上,第三次反面朝上,那么似然函数将会是:
 , 其中T表示反面朝上,
, 其中T表示反面朝上,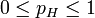 。
。
这时候,似然函数的最大值将会在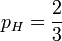 的时候取到。也就是说,当观测到三次投掷中前两次正面朝上而后一次反面朝上时,估计硬币投掷时正面朝上的概率
的时候取到。也就是说,当观测到三次投掷中前两次正面朝上而后一次反面朝上时,估计硬币投掷时正面朝上的概率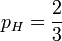 是最合理的。
是最合理的。
我喜欢程序员,他们单纯、固执、容易体会到成就感;面对困难,能够不休不眠;面对压力,能够迎接挑战。他们也会感到困惑与傍徨,但每个程序员的心中都有一个比尔盖茨或是乔布斯的梦想,用智慧把属于自己的事业开创。其实我是一个程序员[=.=]

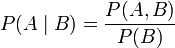
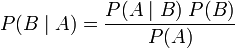
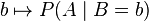
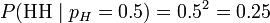




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步