基数估计排重算法在大数据项目中的应用
【摘要】
在大数据项目实践过程中，经常会遇到一种特殊的应用场景，可以归纳为给定一个含有重复元素的有限集合，计算其不重复元素的个数。许多业务需求最终可以归结为基数求解，如网站访问分析中的UV（访客数，指一段时间内访问网站的不同用户的数量）。所谓基数又叫做势，是一个可重复集合中不重复元素的个数。由于数据集基数是不可聚集指标（两个数据集总的基数无法通过分别的基数简单计算），因此如果要得到N个数据集任意组合的基数，需要2N次数据集去重计算，是一个复杂度非常高的计算过程。当数据量较小时，可以采取bitmap“按位或”方法获得较高的计算速度；而当数据量很大时，一般会采取概率算法对基数进行估计。
一、问题的提出
目前，越来越多的项目需要使用大数据方案来解决实际问题，特别是一些统计类的项目。在实际应用过程中，有一类场景十分常见，比如说在某项目中，需要计算某个终端一天内有多少不同用户的访问；计算一天内有多少不同用户使用GPRS服务等。
这类场景如果在普通应用下简单得微不足道，但是在大数据环境下，解决此类问题如果用常规方法会带来时间和空间的巨大资源消耗。如统计每天访问某个终端的不同用户数，每个用户ID包含14个字符，需要用28个字节来表示，1亿个访问用户仅存储就需要2.8G内存，还没包括排重带来的系统开销。那么，有没有一种方法既能占用空间少，又能高效率地完成数据排重运算？
二、解决思路
针对上述问题，我们考虑使用基数估计算法来实现，基数估计算法是一类概率算法，可以在误差可控的前提下以远低于精确计算的时间和空间消耗对基数进行估计。常用的基数估计算法有Linear Counting(LC), LogLog Counting(LLC), Hyper LogLog Counting(HLLC), Adaptive Counting(AC)等，各有各的优缺点，以下着重介绍LC、LLC、HLLC这三种算法。
基本原理如下：首先使用一个良好的哈希函数，将任意数据集映射成服从均匀分布的（伪）随机值。根据这一事实，可以将任意数据集变换为均匀分布的随机数集合。哈希的结果要求：具有良好的均匀性；碰撞几乎可以忽略不计（即哈希结果相同的概率非常小以至于可以忽略不计）；哈希结果是固定长度的。实际中常被用来做基数估计哈希的函数有murmurhash 和lookup3。
LC的基本思路是：设有一哈希函数H，其哈希结果空间有m个值（最小值0，最大值m-1），并且哈希结果服从均匀分布。使用一个长度为m的bitmap，每个bit为一个桶，均初始化为0，设一个集合的基数为n，此集合所有元素通过H哈希到bitmap中，如果某一个元素被哈希到第k个比特并且第k个比特为0，则将其置为1。当集合所有元素哈希完成后，设bitmap中还有u个bit为0。则：
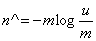
为n的一个估计，且为最大似然估计（MLE）。
LC非常便于合并，在元数据较少时表现特别优秀；误差限一定时，空间复杂度为O(Nmax);缺点是当bitmap满时，此算法会失效。
下面非正式的从直观角度描述LLC算法的思想来源。
设a为待估集合（哈希后）中的一个元素，由上面对H的定义可知，a可以看做一个长度固定的比特串（也就是a的二进制表示），设H哈希后的结果长度为L比特，我们将这L个比特位从左到右分别编号为1、2、…、L：
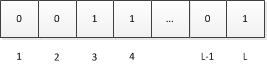
又因为a是从服从均与分布的样本空间中随机抽取的一个样本，因此a每个比特位服从如下分布且相互独立。
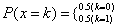
通俗说就是a的每个比特位为0和1的概率各为0.5，且相互之间是独立的。
设ρ(a) 为a的比特串中第一个“1”出现的位置，显然1≤ρ(a)≤L ，这里我们忽略比特串全为0的情况（概率为1/2 L ）。如果我们遍历集合中所有元素的比特串，取ρ max 为所有ρ(a) 的最大值。
此时我们可以将2 ρ max 作为基数的一个粗糙估计，即：
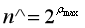
上述分析给出了LLC的基本思想，不过如果直接使用上面的单一估计量进行基数估计会由于偶然性而存在较大误差。因此，LLC采用了分桶平均的思想来消减误差。具体来说，就是将哈希空间平均分成m份，每份称之为一个桶（bucket）。对于每一个元素，其哈希值的前k比特作为桶编号，其中2 k =m ，而后L-k个比特作为真正用于基数估计的比特串。桶编号相同的元素被分配到同一个桶，在进行基数估计时，首先计算每个桶内元素最大的第一个“1”的位置，设为M[i]，然后对这m个值取平均后再进行估计，即：
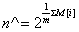
这相当于物理试验中经常使用的多次试验取平均的做法，可以有效消减因偶然性带来的误差。
LC的空间复杂度只有O(log 2 (log 2 (N max ))) ，大大降低了内存的使用空间，而标准误差却能够控制在4%以内。
不过LLC也有自己的问题，就是当基数不太大时，估计值的误差会比较大。这主要是因为当基数不太大时，可能存在一些空桶，这些空桶的ρ max 为0。由于LLC的估计值依赖于各桶ρ max 的几何平均数，而几何平均数对于特殊值（这里就是指0）非常敏感，因此当存在一些空桶时，LLC的估计效果就变得较差。
HLLC的主要改进就是使用调和平均数替代LLC的几何平均数。调和平均数的定义如下：
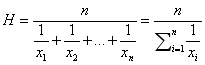
调和平均数可以有效抵抗离群值的扰动。使用调和平均数代替几何平均数后，估计公式变为如下：
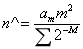
其中：
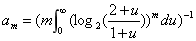
在存储空间相同的情况下，HLLC比LLC具有更高的精度，例如，对于分桶数m为2^13（8k字节）时，LLC的标准误差为1.4%，而HLLC为1.1%。
HLLC在实际应用中，建议采用分段偏差纠正方案对算法进行调整。具体来说，设E为估计值：
当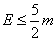 
时，使用LC进行估计。
当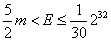
时，使用上面给出的HLLC公式进行估计。
当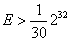
时，估计公式如为
。
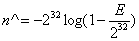三、实践情况
3.1某项目中每天分终端统计不同用户的访问数
3.1.1 小时话单分析
小时定时任务对话单进行分析，保存小时内每个终端访问用户cardinality对象，代码示例如下：
ICardinality card = new HyperLogLog(Constant.Card_log2m);
…
String mdn = val.split("\\|")[2];
card.offer(mdn);
…
Useragent useragentObj = new Useragent();
useragentObj.setCard(card);
然后将对象序列化并保存到分布式文件系统HDFS中。
output.write("useragentStat", new Text(terminal), new UseragentWritable(ua), "/stat/useragent/" + daynow + hournow + "part");
3.1.2 小时话单合并
统计每天各个终端的不同用户的访问数时，需要将当天24小时的cardinality对象进行合并，进一步统计出一天内该终端的不同用户访问数。
ICardinality card = new HyperLogLog(Constant.Card_log2m);
Iterator<UseragentWritable> ite = values.iterator();
while(ite.hasNext())
{
Useragent useragent = ite.next().get();
succ_req_num += useragent.getSuccreqnum();
req_num += useragent.getReqnum();
try
{
card = card.merge(useragent.getCard());
}
catch(CardinalityMergeException e1)
{
LOG.error(e1.getMessage());
e1.printStackTrace();
}
}
3.2某项目中求用户平均流量
3.2.1 小时话单分析
同3.1.1
3.2.2 小时话单合并
同3.1.2，进行小时话单合并，求出一天内不同的用户数。在将一天中的总流量大小除以用户数即可得到用户平均流量。
3.3 hyperloglog算法在不同数据规模下不同分桶数的表现分析
本节主要分析基数排重hyperloglog算法在不同的数据规模（0-2亿）下不同分桶数2P的表现，从而为实际项目在分桶数的选择上提供实验依据。我们对所有数据序列采用32位murmurhash函数进行哈希处理使之呈均匀分布特性。
3.3.1 分桶数(P=10)分析
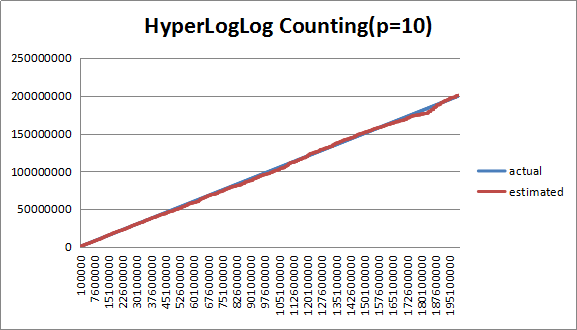
图1 (P=10)下估计值与实际值对比
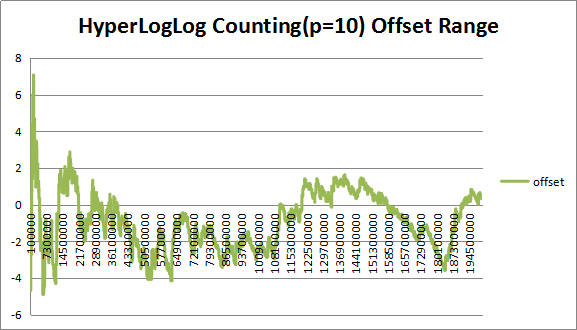
图2 (P=10)下估计值偏差率
从图中可以看出，在P=10下，估计值偏差整体偏大，人为观测大概在3%左右
3.3.2 分桶数(P=12)分析
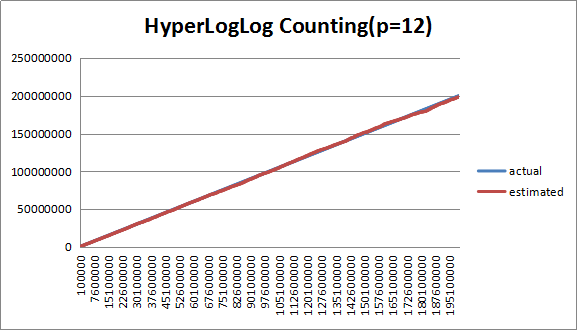
图3 (P=12)下估计值与实际值对比
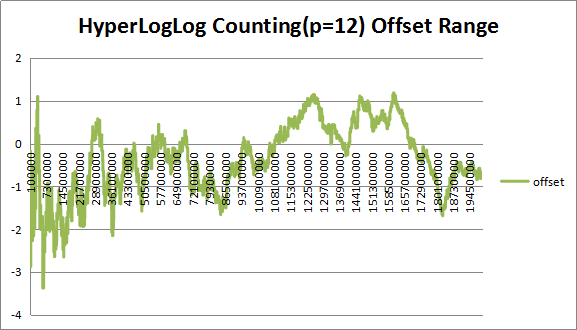
图4 (P=12)下估计值偏差率
从图中可以看出，在P=12下，估计值偏差比P=10明显减小，大概在1.5%左右
3.3.3 分桶数(P=16)分析
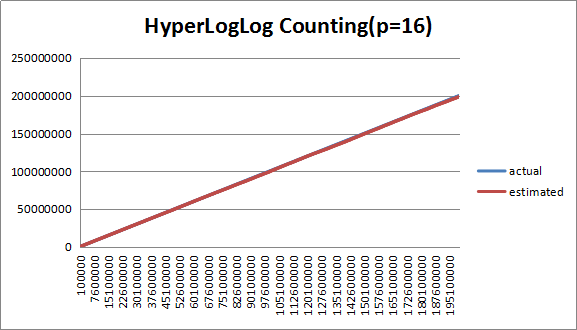
图5 (P=16)下估计值与实际值对比
图6 (P=16)下估计值偏差率
如图所示，在P=16下，估计值偏差进一步减小，大概在0.5%左右，整体走势与实际值吻合较好。
3.3.4 分桶数(P=20)分析
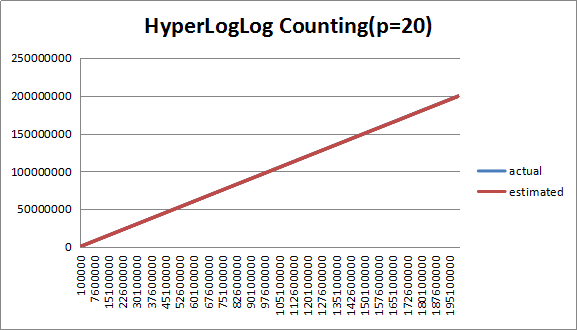
图7 (P=20)下估计值与实际值对比
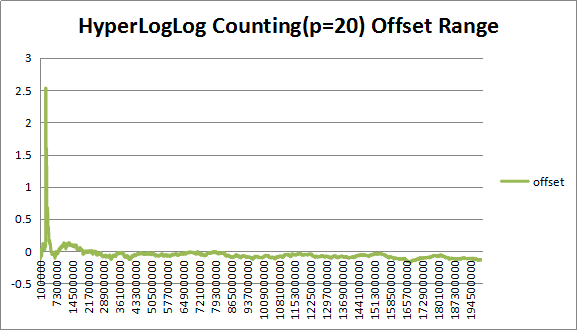
图8 (P=20)下估计值偏差率
如图所示，在P=20下，在大数据规模下，估计值偏差已经很小，在0.2%以下，数据规模在2.5m附近处于LC与HLLC的临界点可以看到有导致误差较大的离群数据，可以得出，在P=20下，HLLC介入过早。
3.3.5 分桶数(P=25)分析
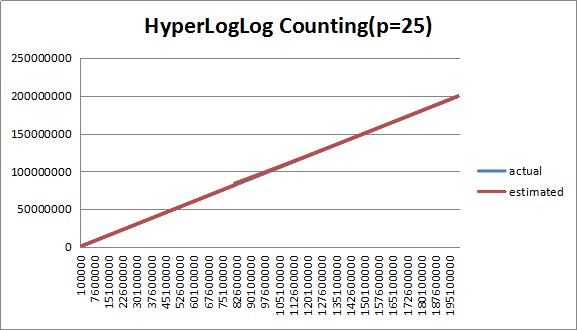
图9 (P=25)下估计值与实际值对比
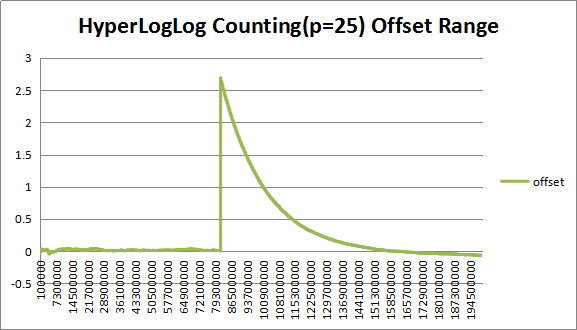
图10 (P=25)下估计值偏差率
如图所示，在P=25下，在大数据规模下，估计值偏差非常小，数据规模在2.5m附近的离群值更加明显，应推迟HLLC的介入。
四、效果评价
实践表明基数估计排重算法使用很少的资源给出数据集基数的一个良好估计，一般只要使用很小的空间存储状态。这个方法和数据本身的特征无关，而且可以高效的进行分布式并行计算，在时间纬度或者空间纬度进行小数据集的基数估计，然后再进行合并，这种特性使得它能够很好地服务于大数据统计分析。实践表明，采用P=16分桶数的HLLC算法可以使标准误差控制在0.5%以下，而整个空间占用却只需要262K.
五、推广建议
此方法适用于对数据结果准确性要求不是特别严格的统计分析，能够容忍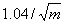
(m为分桶数)的标准误差。
适用于数据集合比较大，而计算存储空间却比较有限，或者计算能力比较有限的数据分析，特别是运用常规排重方法能力达不到或者代价太大的情况。
适用于需要对数据集合进行汇集合并的数据运算，可以进行分布式并行计算，特别适用于大数据环境下的统计分析。
参考资料
《LogLog counting of large cardinalities》
《HyperLogLog: The analysis of a near-optimal cardinality estimation algorithm》
《Damn Cool Algorithms: Cardinality Estimation》
http://blog.notdot.net/2012/09/Dam-Cool-Algorithms-Cardinality-Estimation
http://blog.codinglabs.org/articles/
