优化算法-BFGS

  BGFS是一种准牛顿算法, 所谓的"准"是指牛顿算法会使用Hessian矩阵来进行优化, 但是直接计算Hessian矩阵比较麻烦, 所以很多算法会使用近似的Hessian, 这些算法就称作准牛顿算法(Quasi Newton Algorithm).

  1. 牛顿算法(Newton Algorithm)

  牛顿算法考虑了函数的二阶单数, 是一种二阶优化方法, 并且是所有其他二阶优化方法的鼻祖. 作为对比, 梯度下降(Gradient Descent)只考虑了函数的一阶导数, 是一阶优化方法. 

  推导过程：

  我们考虑函数的二阶泰勒展开式: \(\mathit{f_{quad}}(\mathit{\boldsymbol{\theta}})=\mathit{f_k}+\mathit{\boldsymbol{g}_k^T}(\mathit{\boldsymbol{\theta}-\boldsymbol{\theta}_k})+\frac{1}{2}(\mathit{\boldsymbol{\theta}-\boldsymbol{\theta}_k})^{\mathit{T}}\boldsymbol{H}_{\mathit{k}}(\mathit{\boldsymbol{\theta}-\boldsymbol{\theta}_k})\), 其中\(\mathit{\boldsymbol{\theta}}\)为需要优化的参数, \(\boldsymbol{g}_k\)为\(\nabla \mathit{f}(\mathit{\boldsymbol{\theta}_k})\)

  上式可以重写作:$$\mathit{f_{quad}}(\mathit{\theta}) = \mathit{\boldsymbol{\theta}^T}\boldsymbol{A}\mathit{\boldsymbol{\theta}}+\boldsymbol{b}^T\mathit{\boldsymbol{\theta}}+\mathit{c}$$

  其中

    式子-1

  二次函数的最小值取为\(x=-\frac{b}{2a}\)

  所以式子-1在\(\mathit{\boldsymbol{\theta}}\)取以下值时达到最小

  

  亦即Newton算法每次迭代时只需要对\(\mathit{\boldsymbol{\theta}_k}\)加上以下项

  

  牛顿方法的步骤为

  2. BFGS算法

  Newton算法在计算时需要用到Hessian矩阵\(\boldsymbol{H}\), 计算Hessian矩阵非常费时, 所以研究者提出了很多使用方法来近似Hessian矩阵, 这些方法都称作准牛顿算法, BFGS就是其中的一种, 以其发明者Broyden, Fletcher, Goldfarb和Shanno命名.

  BFGS算法使用以下方法来近似Hessian矩阵, \(\boldsymbol{B}_k \approx \boldsymbol{H}_k\):

  

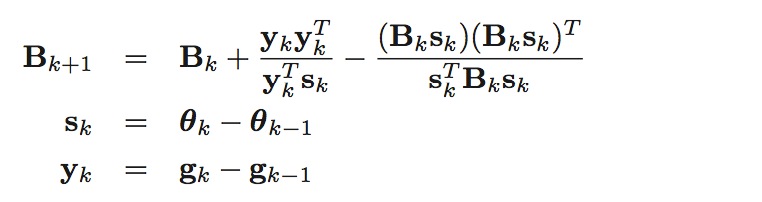
  初始时可以取\(\boldsymbol{B}_0=\boldsymbol{I}\)

  因为Hessian矩阵的大小为\(\mathit{O}(\mathit{D}^2)\), 其中D为参数的个数, 所以有时Hessian矩阵会比较大, 可以使用L-BFGS(Limited-memory BFGS)算法来进行优化.

  参考文献:

  [1]. Machine Learning: A Probabilistic Perspective. p249-p252.

  [2]. Wekipedia: L-BFGS