时间序列挖掘-DTW加速算法FastDTW简介
本文地址为：http://www.cnblogs.com/kemaswill/，作者联系方式为kemaswill@163.com,转载请注明出处。
关于DTW算法的简介请见我的上一篇博客：时间序列挖掘-动态时间归整算法原理和实现。
DTW采用动态规划来计算两个时间序列之间的相似性，算法复杂度为O(N2)。当两个时间序列都比较长时，DTW算法效率比较慢，不能满足需求，为此，有许多对DTW进行加速的算法：FastDTW,SparseDTW,LB_Keogh,LB_Improved等。在这里我们介绍FastDTW。
1. 标准DTW算法
在DTW中，我们要寻找的是一个归整路径(详见时间序列挖掘-动态时间归整算法原理和实现)，如下图所示：
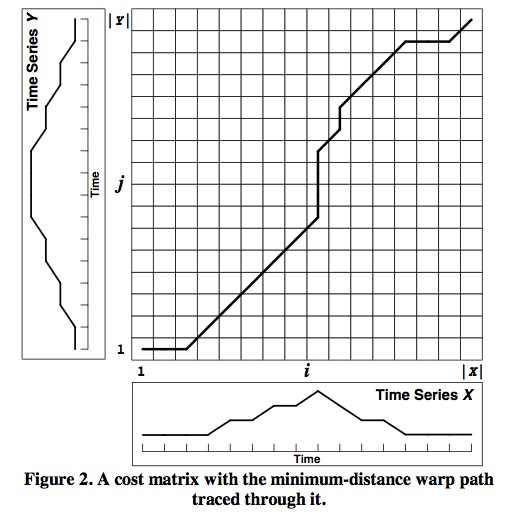
最终我们想要得到的是这条路径经过的所有点的坐标(i,j)对应的X和Y两个时间序列的点Xi和Yj的距离(比如欧几里得距离)之和，亦即我们需要求得代价矩阵最右上角的元素D(i,j)。而根据动态规划的思想：
要求得D(i,j)必须要知道D(i-1,j), D(i-1,j-1), D(i,j-1)等，以此类推，我们需要求得整个D矩阵，才能得到最终的D(i,j)，亦即算法的时间复杂度为O(N2)。
2. DTW常用加速手段
常用的DTW加速手段有：
(1). 限制。亦即减少D的搜索空间，下图中阴影部分为实际的探索空间，空白的部分不进行探索。
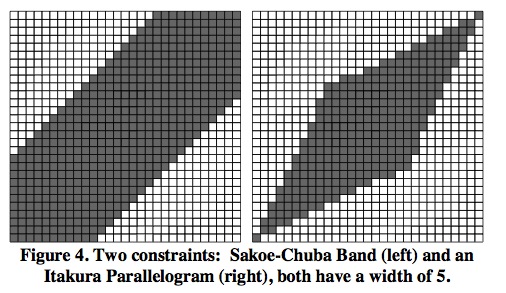
(2). 数据抽象。亦即把之前长度为N的时间序列规约成长度为M(M<N)表述方式：
(3). 索引。索引是在进行分类和聚类时减少需要运行的DTW的次数的方法，并不能加速一次的DTW计算。
3. FastDTW
FastDTW综合使用限制和数据抽象两种方法来加速DTW的计算，主要分为三个步骤：
(1). 粗粒度化。亦即首先对原始的时间序列进行数据抽象，数据抽象可以迭代执行多次1/1->1/2->1/4->1/16，粗粒度数据点是其对应的多个细粒度数据点的平均值。
(2). 投影。在较粗粒度上对时间序列运行DTW算法。
(3). 细粒度化。将在较粗粒度上得到的归整路径经过的方格进一步细粒度化到较细粒度的时间序列上。除了进行细粒度化之外，我们还额外的在较细粒度的空间内额外向外(横向，竖向，斜向)扩展K个粒度，K为半径参数，一般取为1或者2.
FastDTW算法的具体执行流程如下图所示:
第一个图表示在较粗粒度空间(1/8)内执行DTW算法。第二个图表示将较粗粒度空间(1/8)内求得的归整路径经过的方格细粒度化，并且向外(横向，竖向，斜向)扩展一个(由半径参数确定)细粒度单位后，再执行DTW得到的归整路径。第三个图和第四个图也是这样。
由于采取了减少搜索空间的策略，FastDTW并不一定能够求得准确的DTW距离，但是FastDTW算法的时间复杂度比较低，为O(N)。
参考文献：
[1]. FastDTW: Toward Accurate Dynamic Time Warping in Linear Time and Space. Stan Salvador, Philip Chan.
