poj 1151 Atlantis】线段树之扫描线（面积并）

题目链接：http://poj.org/problem?id=1151

题目大意： 给你n个矩形，求他们的总面积之和。

解题思路：

      这是我写的线段树扫描线第一题，搜狗了一下，说实话网上的解释都很抽象，昨晚用手机百度一下看到了一张让人一看就有灵感的扫描线图，今天找了很久都没找到那张图了，本来还想copy一下给大家分享来着。

    哈哈，不过大家别急，为了方便描述，自己动手画了几个。

     

    

  

   

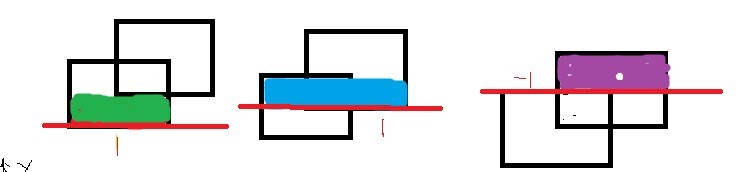
   四条红线为矩形的上下底边，这里我们称之为扫描线（实际编程中不存在，只是一个概念）。

   如图所示，要求两个矩形的面积并，可以把矩形分成几个小矩形，最后的面积总和为它们的和。

   对于每个小矩形其 面积S=长*宽。宽就是两条扫描线之间y的差值，这里留给我们的问题就是如何求长了。

   因为x是double型而且比较大，所以首先对x进行离散化，x数组下标对应实际的x。

   然后就开始建树了，建树比较简单，主要的问题在于如何进行更新树。我在这里卡了好久，要注意实际的扫描线长度随时可能变化，并不是相同的，唯一不变的就行要更新数的左右区间（即矩形的底边长度）。

   因为扫描线是会变的，所以这里才是我们要重点解决的问题，怎么办？哈哈，这里引出我们伟大的标记变量cover， 对于每个矩形下底边标记为1，上底边标记为-1。当一根线扫描到下一根线的时候，cover值会覆盖相应的区间，被覆盖的区间flag值会加上此扫描线的cover（可能为正也可能为负）值，这里最好动手自己模拟一下。所以重叠位置（flag>2）就算遇见负的cover它的flag依然是正的！！

   重点要提的是：覆盖区间只在总区间上变化，总区间一直保持不变。   

    PS： 还是看不懂的话看着代码理解吧，我就是这样过来的。

   对扫描线进行y从小到大排序，然后从下往上扫描。

 

   

View Code 
  1 #include <iostream>
  2 #include <cstdio>
  3 #include <cstring>
  4 #include <algorithm>
  5 using namespace std;
  6 
  7 #define lz 2*u,l,mid
  8 #define rz 2*u+1,mid+1,r
  9 const int maxn=4222;
 10 double sum[maxn];
 11 int flag[maxn];
 12 double X[maxn];
 13 
 14 struct Node
 15 {
 16     double lx, rx, y;
 17     int s;
 18     Node(){};
 19     Node(double lx_, double rx_, double y_, int s_)
 20     {
 21         lx=lx_, rx=rx_, y=y_, s=s_;
 22     }
 23     bool operator <(const Node &S) const
 24     {
 25         return y<S.y;
 26     }
 27 }line[maxn];
 28 
 29 int find(double tmp, int n)
 30 {
 31     int l=1, r=n, mid;
 32     while(l<=r)
 33     {
 34         mid=(l+r)>>1;
 35         if(X[mid]==tmp) return mid;
 36         else if(X[mid]<tmp) l=mid+1;
 37         else r=mid-1;
 38     }
 39 }
 40 
 41 void push_up(int u, int l, int r)
 42 {
 43     if(flag[u]) sum[u]=X[r+1]-X[l];
 44     else if(l==r) sum[u]=0;
 45     else sum[u]=sum[2*u]+sum[2*u+1];
 46 }
 47 
 48 void Update(int u, int l, int r, int tl, int tr, int c)
 49 {
 50     if(tl<=l&&r<=tr)
 51     {
 52         flag[u]+=c;
 53         push_up(u,l,r);
 54         return ;
 55     }
 56     int mid=(l+r)>>1;
 57     if(tr<=mid) Update(lz,tl,tr,c);
 58     else if(tl>mid) Update(rz,tl,tr,c);
 59     else
 60     {
 61         Update(lz,tl,mid,c);
 62         Update(rz,mid+1,tr,c);
 63     }
 64     push_up(u,l,r);
 65 }
 66 
 67 int main()
 68 {
 69     int n,tcase=0;
 70     while(cin >> n,n)
 71     {
 72         int num=0;
 73         memset(flag,0,sizeof(flag));
 74         memset(sum,0,sizeof(sum));
 75         for(int i=0; i<n; i++)
 76         {
 77             double x1,x2,y1,y2;
 78             scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
 79             line[++num]=Node(x1,x2,y1,1);
 80             X[num]=x1;
 81             line[++num]=Node(x1,x2,y2,-1);
 82             X[num]=x2;
 83         }
 84         sort(X+1,X+num+1);
 85         sort(line+1,line+num+1);
 86         int k=1;
 87         for(int i=2; i<=num; i++)
 88             if(X[i]!=X[i+1]) X[++k]=X[i];
 89         double ans=0;
 90         for(int i=1; i<num; i++)
 91         {
 92             int l=find(line[i].lx,k);
 93             int r=find(line[i].rx,k)-1;
 94             Update(1,1,k,l,r,line[i].s);
 95             ans+=sum[1]*(line[i+1].y-line[i].y);
 96         }
 97         printf("Test case #%d\n",++tcase);
 98         printf("Total explored area: %.2lf\n\n",ans);
 99     }
100     return 0;
101 }

 

      

      

posted @ 2013-02-26 20:43  Mr. Ant  阅读(5546)  评论(2)  编辑  收藏  举报