图的遍历
定义结点
struct MGraph { int vexs[MAXVEX]; //顶点数 int arc[MAXVEX][MAXVEX]; //邻接矩阵 int numVertex, numEdges; //定点数 边数 };
深度优先遍历
图示
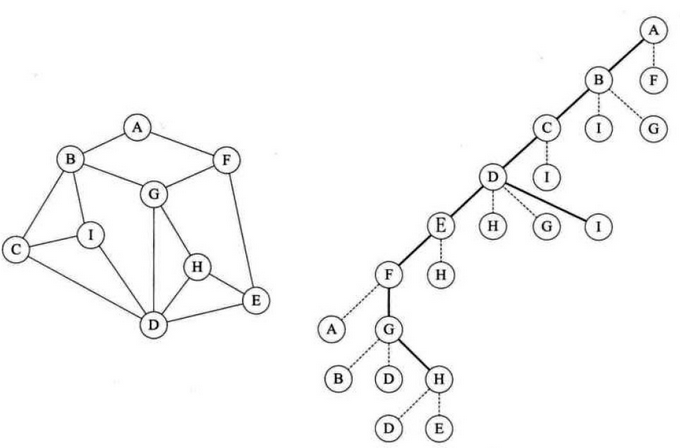
参考代码
bool visited[MAX]; void DFS(MGraph G, int i) { cout << G.vexs[i] << " ";
visited[i] = true; for (int j = 0; j < G.numVertex; ++j) { if (G.arc[i][j] == 1 && !visited[j]) DFS(G, j); } } void DFSTranverse(MGraph G) { for (int i = 0; i < G.numVertex; ++i) visited[i] = false; for (int i = 0 ; i < G.numVertex; ++i) //如果是连通图,只执行一次 { if (!visited[i]) DFS(G, i); } }
广度优先遍历
图示
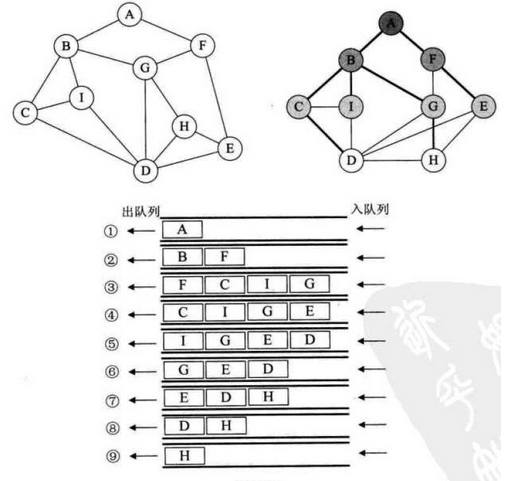
参考代码
void BFSTranverse(MGraph G) { queue<int> q; bool visited[G.numVertex]; for (int i = 0; i < G.numVertex; ++i) visited[i] = false; for (int i = 0; i < G.numVertex; ++i) { if (!visited[i]) { cout << G.vexs[i] << " "; q.push(i); visited[i] = true; while (!q.empty()) { int k = q.top(); q.pop(); for (int j = 0; j < G.numVertex; ++j) { if (G.arc[i][j] == 1 && !visitied(j)) { cout << G.vexs[j] << " "; visited[j] = true; q.push(j); } } } }
}//for }



