找出有序数组中绝对值最小的数

假设数组是从小到大排序，数值可能为负数、0、正数。

思路一

可以一次性遍历一遍，找出绝对值最小值，此时时间复杂度为O(N)，缺点是没有利用数组是有序的这一特点。

 

思路二

数组有序，可以利用二分查找的特性。中间的数是正数，往后找；中间的数是负数，往前找。

问题的本质是找到正数的最小值，或负数的最大值，分析以下集中情况

数组为a[]， 数组大小为n.

• n=1，没有商量的余地，直接返回
• a[0] * a[n-1] >= 0，说明这些元素同为非正或同为非负。要是a[0]>=0，返回a[0]；否则返回a[n-1]
• a[0] * a[n-1] < 0，说明这些元素中既有整数，也有负数。此时需要计算中间位置为mid = low + high/2，如果a[mid]*a[low] >=0说明a[mid]也为非正，缩小范围low=mid；如果a[mid]*a[high]>=0，说明a[mid]非负，缩小范围high=mid。在期间如果还有两个元素，那么就比较以下他俩，直接返回了

参考代码

#include <iostream>
#include <cmath>
using namespace std;

int absMin(int *a, int size)
{
    if(size == 1)
        return a[0];
    if(a[0] * a[size-1] >= 0)
        return (a[0] >= 0) ? a[0] : a[size-1];
    else
    {
        int low = 0, high = size-1, mid;
        while(low < high)
        {
            if(low + 1 == high)
                return abs(a[low]) < abs(a[high]) ? a[low] : a[high];
            mid = low + (high - low) / 2;
            if(a[low] * a[mid] >= 0)
                low = mid;
            if(a[high] * a[mid] >= 0)
                high = mid;
        }
    }
}

int main()
{
    int arr1[] = {-8, -3, -1, 2, 5, 7, 10};
    size_t size1 = sizeof(arr1) / sizeof(int);
    int minabs1 = absMin(arr1, size1);
    cout << "Result:" << minabs1 << endl;

    int arr2[] = {-8, -3, 2, 5, 7, 10};
    size_t size2 = sizeof(arr2) / sizeof(int);
    int minabs2 = absMin(arr2, size2);
    cout << "Result:" << minabs2 << endl;
}

结果

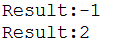
复杂度分析

时间复杂度O(log2n)，空间复杂度O(1).

 ===========================================

改进1：完全可以把这些特例（size=1、同号，放到while循环里）

============================================

int absMin(int *a, int size)
{
    int low = 0, high = size-1, mid;
    while(low <= high)
    {
        if(a[low] * a[high] >= 0)
            return (a[low] >= 0) ? a[low] : a[high]; 
        if(low + 1 == high)
            return abs(a[low]) < abs(a[high]) ? a[low] : a[high];
        mid = low + (high - low) / 2;
        if(a[low] * a[mid] >= 0)
            low = mid;
        if(a[high] * a[mid] >= 0)
            high = mid;
    }
    cout << "ERROR, size <= 0" << endl;
    return -1; //size <= 0
}

 

拓展

有序（自小到达）绝对值最大呢？

如果有整数、0、负数的话，绝对值最小值在相对中间部位。但是如果求绝对值最大，绝对在两边，例如

1. 1 2 3 4 
2. -4 -3 -2 -1
3. -4 -2 0 1 2

因此只需比较边上的两个值的绝对值大小，方可揭晓答案。