Javascript图像处理——平滑处理
2012-12-28 09:10 Justany_WhiteSnow 阅读(5708) 评论(13) 收藏 举报前言
上一篇文章,我们讲解了图像的虚拟边缘,这篇文章开始进行平滑(也就是模糊)处理。
基本原理
这里直接引用OpenCV 2.4+ C++ 平滑处理和OpenCV 2.4+ C++ 边缘梯度计算的相关内容:
平滑也称模糊, 是一项简单且使用频率很高的图像处理方法。
平滑处理时需要用到一个滤波器。 最常用的滤波器是线性滤波器,线性滤波处理的输出像素值(例如:
)是输入像素值(例如:
)的加权平均:
称为核, 它仅仅是一个加权系数。
这里涉及一种叫做“卷积”的运算,那么卷积是什么呢?
卷积是在每一个图像块与某个算子(核)之间进行的运算。
核?!
核就是一个固定大小的数值数组。该数组带有一个锚点 ,一般位于数组中央。

可是这怎么运算啊?
假如你想得到图像的某个特定位置的卷积值,可用下列方法计算:
- 将核的锚点放在该特定位置的像素上,同时,核内的其他值与该像素邻域的各像素重合;
- 将核内各值与相应像素值相乘,并将乘积相加;
- 将所得结果放到与锚点对应的像素上;
- 对图像所有像素重复上述过程。
用公式表示上述过程如下:
在图像边缘的卷积怎么办呢?
计算卷积前,需要通过复制源图像的边界创建虚拟像素,这样边缘的地方也有足够像素计算卷积了。这就是为什么上一篇文章需要做虚拟边缘函数。
均值平滑
均值平滑实际上就是内核元素全是1的卷积运算,然后再除以内核的大小,用数学表达式来表示就是:

下面我们来实现均值平滑函数blur:
function blur(__src, __size1, __size2, __borderType, __dst){ if(__src.type && __src.type == "CV_RGBA"){ var height = __src.row, width = __src.col, dst = __dst || new Mat(height, width, CV_RGBA), dstData = dst.data; var size1 = __size1 || 3, size2 = __size2 || size1, size = size1 * size2; if(size1 % 2 !== 1 || size2 % 2 !== 1){ console.error("size大小必须是奇数"); return __src; } var startX = Math.floor(size1 / 2), startY = Math.floor(size2 / 2); var withBorderMat = copyMakeBorder(__src, startY, startX, 0, 0, __borderType), mData = withBorderMat.data, mWidth = withBorderMat.col; var newValue, nowX, offsetY, offsetI; var i, j, c, y, x; for(i = height; i--;){ offsetI = i * width; for(j = width; j--;){ for(c = 3; c--;){ newValue = 0; for(y = size2; y--;){ offsetY = (y + i) * mWidth * 4; for(x = size1; x--;){ nowX = (x + j) * 4 + c; newValue += mData[offsetY + nowX]; } } dstData[(j + offsetI) * 4 + c] = newValue / size; } dstData[(j + offsetI) * 4 + 3] = mData[offsetY + startY * mWidth * 4 + (j + startX) * 4 + 3]; } } }else{ console.error("不支持类型。"); } return dst; }
其中size1和size2分别是核的横向和纵向大小,并且必须是正奇数。
高斯平滑
最有用的滤波器 (尽管不是最快的)。 高斯滤波是将输入数组的每一个像素点与高斯内核卷积将卷积和当作输出像素值。

参考一维高斯函数,我们可以看见,他是个中间大两边小的函数。
所以高斯滤波器其加权数是中间大,四周小的。
其二维高斯函数为:

其中  为均值 (峰值对应位置),
为均值 (峰值对应位置), 代表标准差 (变量
代表标准差 (变量 和 变量
和 变量 各有一个均值,也各有一个标准差)。
各有一个均值,也各有一个标准差)。
这里参考OpenCV的实现,不过应该还有优化空间,因为还没用到分离滤波器。
首先我们做一个getGaussianKernel来返回高斯滤波器的一维数组。
function getGaussianKernel(__n, __sigma){ var SMALL_GAUSSIAN_SIZE = 7, smallGaussianTab = [[1], [0.25, 0.5, 0.25], [0.0625, 0.25, 0.375, 0.25, 0.0625], [0.03125, 0.109375, 0.21875, 0.28125, 0.21875, 0.109375, 0.03125] ]; var fixedKernel = __n & 2 == 1 && __n <= SMALL_GAUSSIAN_SIZE && __sigma <= 0 ? smallGaussianTab[__n >> 1] : 0; var sigmaX = __sigma > 0 ? __sigma : ((__n - 1) * 0.5 - 1) * 0.3 + 0.8, scale2X = -0.5 / (sigmaX * sigmaX), sum = 0; var i, x, t, kernel = []; for(i = 0; i < __n; i++){ x = i - (__n - 1) * 0.5; t = fixedKernel ? fixedKernel[i] : Math.exp(scale2X * x * x); kernel[i] = t; sum += t; } sum = 1 / sum; for(i = __n; i--;){ kernel[i] *= sum; } return kernel; };
然后通过两个这个一维数组,便可以计算出一个完整的高斯内核,再利用blur里面用到的循环方法,就可以算出高斯平滑后的矩阵了。
function GaussianBlur(__src, __size1, __size2, __sigma1, __sigma2, __borderType, __dst){ if(__src.type && __src.type == "CV_RGBA"){ var height = __src.row, width = __src.col, dst = __dst || new Mat(height, width, CV_RGBA), dstData = dst.data; var sigma1 = __sigma1 || 0, sigma2 = __sigma2 || __sigma1; var size1 = __size1 || Math.round(sigma1 * 6 + 1) | 1, size2 = __size2 || Math.round(sigma2 * 6 + 1) | 1, size = size1 * size2; if(size1 % 2 !== 1 || size2 % 2 !== 1){ console.error("size必须是奇数。"); return __src; } var startX = Math.floor(size1 / 2), startY = Math.floor(size2 / 2); var withBorderMat = copyMakeBorder(__src, startY, startX, 0, 0, __borderType), mData = withBorderMat.data, mWidth = withBorderMat.col; var kernel1 = getGaussianKernel(size1, sigma1), kernel2, kernel = new Array(size1 * size2); if(size1 === size2 && sigma1 === sigma2) kernel2 = kernel1; else kernel2 = getGaussianKernel(size2, sigma2); var i, j, c, y, x; for(i = kernel2.length; i--;){ for(j = kernel1.length; j--;){ kernel[i * size1 + j] = kernel2[i] * kernel1[j]; } } var newValue, nowX, offsetY, offsetI; for(i = height; i--;){ offsetI = i * width; for(j = width; j--;){ for(c = 3; c--;){ newValue = 0; for(y = size2; y--;){ offsetY = (y + i) * mWidth * 4; for(x = size1; x--;){ nowX = (x + j) * 4 + c; newValue += (mData[offsetY + nowX] * kernel[y * size1 + x]); } } dstData[(j + offsetI) * 4 + c] = newValue; } dstData[(j + offsetI) * 4 + 3] = mData[offsetY + startY * mWidth * 4 + (j + startX) * 4 + 3]; } } }else{ console.error("不支持的类型"); } return dst; }
中值平滑
中值滤波将图像的每个像素用邻域 (以当前像素为中心的正方形区域)像素的中值代替 。
依然使用blur里面用到的循环,只要得到核中的所有值,再通过sort排序便可以得到中值,然后锚点由该值替代。
function medianBlur(__src, __size1, __size2, __borderType, __dst){ if(__src.type && __src.type == "CV_RGBA"){ var height = __src.row, width = __src.col, dst = __dst || new Mat(height, width, CV_RGBA), dstData = dst.data; var size1 = __size1 || 3, size2 = __size2 || size1, size = size1 * size2; if(size1 % 2 !== 1 || size2 % 2 !== 1){ console.error("size必须是奇数"); return __src; } var startX = Math.floor(size1 / 2), startY = Math.floor(size2 / 2); var withBorderMat = copyMakeBorder(__src, startY, startX, 0, 0, __borderType), mData = withBorderMat.data, mWidth = withBorderMat.col; var newValue = [], nowX, offsetY, offsetI; var i, j, c, y, x; for(i = height; i--;){ offsetI = i * width; for(j = width; j--;){ for(c = 3; c--;){ for(y = size2; y--;){ offsetY = (y + i) * mWidth * 4; for(x = size1; x--;){ nowX = (x + j) * 4 + c; newValue[y * size1 + x] = mData[offsetY + nowX]; } } newValue.sort(function(a, b){return a - b;}); dstData[(j + offsetI) * 4 + c] = newValue[Math.round(size / 2)]; } dstData[(j + offsetI) * 4 + 3] = mData[offsetY + startY * mWidth * 4 + (j + startX) * 4 + 3]; } } }else{ console.error("类型不支持"); } return dst; };
更多例子
系列目录
参考资料
opencv源码解析之(4):GaussianBlur() . tornadomeet . 2012-03-10

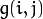 )是输入像素值(例如:
)是输入像素值(例如: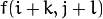 )的加权平均:
)的加权平均:
 称为核
称为核

 浙公网安备 33010602011771号
浙公网安备 33010602011771号