多边形重心

给定一个多边形：如何求重心？？

 

三角形的重心是： (x1+x2+x3) / 3，(y1+y2+y3) / 3（质点系重心公式）

 

 

一个由 N 个顶点( x_i , y_i ) 确定的不自交闭多边形的中心能如下计算:

记号 ( x_N , y_N )与顶点 ( x₀ , y₀ )相同。多边形的面积为：

多边形的中心由下式给出：

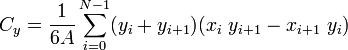
推论过程：

将多边形剖分成N个三角形，分别求出其重心和面积，这时可以想象，原来质量均匀分布在内部区域上，而现在质量仅仅分布在这N个重心点上（等假变换），这时候就可以利用刚才的质点系重心公式了。 不过，要稍微改一改，改成加权平均数，因为质量不是均匀分布的，每个质点代表其所在三角形，其质量就是该三角形的面积（有向面积！），——这就是权！

 

所以 :

　　Cx = Sigma(X i + X i+1) / 3 * ( Xi Yi+1 - Xi+1 Yi) / 2 / SumArea  (i = 0,1,2.....n-1) ;

                  

 例题：  http://acm.hdu.edu.cn/showproblem.php?pid=1115

#include<stdio.h>

struct Point{
	int x, y;
}p[1000100] ;

int main(){
	int T ;
	scanf("%d",&T) ;
	while(T--){
		int n;
		scanf("%d",&n) ;
		for(int i=1;i<=n;i++)
			scanf("%d%d",&p[i].x,&p[i].y) ;
		p[0].x = p[n].x ; p[0].y = p[n].y ;
		double A = 0, x = 0, y = 0, area ;
		for(int i=0;i<n;i++){
			area = (p[i].x * p[i+1].y - p[i].y * p[i+1].x) ;
			A += area ;
			x += (long long)(p[i].x + p[i+1].x) * area ;
			y += (long long)(p[i].y + p[i+1].y) * area ;
		}
		x = x / A / 3 ;
		y = y / A / 3 ;
		printf("%.2lf %.2lf\n",x ,y) ;
	}
	return 0;
}