增强学习（四） ----- 蒙特卡罗方法(Monte Carlo Methods)

1. 蒙特卡罗方法的基本思想

蒙特卡罗方法又叫统计模拟方法，它使用随机数（或伪随机数）来解决计算的问题，是一类重要的数值计算方法。该方法的名字来源于世界著名的赌城蒙特卡罗，而蒙特卡罗方法正是以概率为基础的方法。

一个简单的例子可以解释蒙特卡罗方法，假设我们需要计算一个不规则图形的面积，那么图形的不规则程度和分析性计算（比如积分）的复杂程度是成正比的。而采用蒙特卡罗方法是怎么计算的呢？首先你把图形放到一个已知面积的方框内，然后假想你有一些豆子，把豆子均匀地朝这个方框内撒，散好后数这个图形之中有多少颗豆子，再根据图形内外豆子的比例来计算面积。当你的豆子越小，撒的越多的时候，结果就越精确。

2. 增强学习中的蒙特卡罗方法

现在我们开始讲解增强学习中的蒙特卡罗方法，与上篇的DP不同的是，这里不需要对环境的完整知识。蒙特卡罗方法仅仅需要经验就可以求解最优策略，这些经验可以在线获得或者根据某种模拟机制获得。

要注意的是，我们仅将蒙特卡罗方法定义在episode task上，所谓的episode task就是指不管采取哪种策略π，都会在有限时间内到达终止状态并获得回报的任务。比如玩棋类游戏，在有限步数以后总能达到输赢或者平局的结果并获得相应回报。

那么什么是经验呢？经验其实就是训练样本。比如在初始状态s，遵循策略π，最终获得了总回报R，这就是一个样本。如果我们有许多这样的样本，就可以估计在状态s下，遵循策略π的期望回报，也就是状态值函数V^π(s)了。蒙特卡罗方法就是依靠样本的平均回报来解决增强学习问题的。

尽管蒙特卡罗方法和动态规划方法存在诸多不同，但是蒙特卡罗方法借鉴了很多动态规划中的思想。在动态规划中我们首先进行策略估计，计算特定策略π对应的V^π和Q^π，然后进行策略改进，最终形成策略迭代。这些想法同样在蒙特卡罗方法中应用。

3. 蒙特卡罗策略估计(Monte Carlo Policy evalution)

首先考虑用蒙特卡罗方法来学习状态值函数V^π(s)。如上所述，估计V^π(s)的一个明显的方法是对于所有到达过该状态的回报取平均值。这里又分为first-visit MC methods和every-visit MC methods。这里，我们只考虑first MC methods，即在一个episode内，我们只记录s的第一次访问，并对它取平均回报。

现在我们假设有如下一些样本，取折扣因子γ=1，即直接计算累积回报，则有

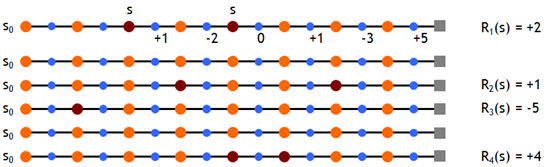
根据first MC methods，对出现过状态s的episode的累积回报取均值，有V^π(s)≈ (2 + 1 – 5 + 4)/4 = 0.5

    容易知道，当我们经过无穷多的episode后，V^π(s)的估计值将收敛于其真实值。

4. 动作值函数的MC估计(Mote Carlo Estimation of Action Values)

在状态转移概率p(s'|a,s)已知的情况下，策略估计后有了新的值函数，我们就可以进行策略改进了，只需要看哪个动作能获得最大的期望累积回报就可以。然而在没有准确的状态转移概率的情况下这是不可行的。为此，我们需要估计动作值函数Q^π(s,a)。Q^π(s,a)的估计方法前面类似，即在状态s下采用动作a，后续遵循策略π获得的期望累积回报即为Q^π(s,a)，依然用平均回报来估计它。有了Q值，就可以进行策略改进了

5. 持续探索(Maintaining Exploration)

下面我们来探讨一下Maintaining Exploration的问题。前面我们讲到，我们通过一些样本来估计Q和V，并且在未来执行估值最大的动作。这里就存在一个问题，假设在某个确定状态s₀下，能执行a₀, a₁, a₂这三个动作，如果智能体已经估计了两个Q函数值，如Q(s₀,a₀), Q(s₀,a₁)，且Q(s₀,a₀)>Q(s₀,a₁)，那么它在未来将只会执行一个确定的动作a₀。这样我们就无法更新Q(s₀,a₁)的估值和获得Q(s₀,a₂)的估值了。这样的后果是，我们无法保证Q(s₀,a₀)就是s₀下最大的Q函数。

Maintaining Exploration的思想很简单，就是用soft policies来替换确定性策略，使所有的动作都有可能被执行。比如其中的一种方法是ε-greedy policy，即在所有的状态下，用1-ε的概率来执行当前的最优动作a₀，ε的概率来执行其他动作a₁, a₂。这样我们就可以获得所有动作的估计值，然后通过慢慢减少ε值，最终使算法收敛，并得到最优策略。简单起见，在下面MC控制中，我们使用exploring start，即仅在第一步令所有的a都有一个非零的概率被选中。

6. 蒙特卡罗控制(Mote Carlo Control)

我们看下MC版本的策略迭代过程：

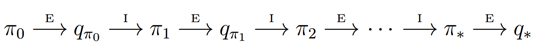
根据前面的说法，值函数Q^π(s,a)的估计值需要在无穷多episode后才能收敛到其真实值。这样的话策略迭代必然是低效的。在上一篇DP中，我们了值迭代算法，即每次都不用完整的策略估计，而仅仅使用值函数的近似值进行迭代，这里也用到了类似的思想。每次策略的近似值，然后用这个近似值来更新得到一个近似的策略，并最终收敛到最优策略。这个思想称为广义策略迭代。

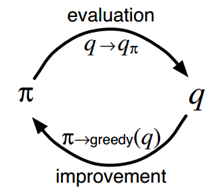
具体到MC control，就是在每个episode后都重新估计下动作值函数（尽管不是真实值），然后根据近似的动作值函数，进行策略更新。这是一个episode by episode的过程。

一个采用exploring starts的Monte Carlo control算法，如下图所示，称为Monte Carlo ES。而对于所有状态都采用soft policy的版本，这里不再讨论。

7. 小结

Monte Carlo方法的一个显而易见的好处就是我们不需要环境模型了，可以从经验中直接学到策略。它的另一个好处是，它对所有状态s的估计都是独立的，而不依赖与其他状态的值函数。在很多时候，我们不需要对所有状态值进行估计，这种情况下蒙特卡罗方法就十分适用。

不过，现在增强学习中，直接使用MC方法的情况比较少，而较多的采用TD算法族。但是如同DP一样，MC方法也是增强学习的基础之一，因此依然有学习的必要。

 

参考资料：

[1] R.Sutton et al. Reinforcement learning: An introduction, 1998

[2] Wikipedia，蒙特卡罗方法