[知识点]树链剖分

// 此博文为迁移而来，写于2015年7月11日，不代表本人现在的观点与看法。原始地址：http://blog.sina.com.cn/s/blog_6022c4720102w69l.html

 

UPDATE（20180824）：进行多处修正，并添加多处注释，代码重写。感谢评论区的建议。

 

一、前言

树链剖分，一个高大上的名字。树链，即树上的路径，现在我们的任务是所谓的剖分。所以我们可以看出，树链剖分并不是一种单独的数据结构，不像堆，线段树等等，而是直接在一棵普通的树上处理，然而单是这一课树是并没有什么卵用的。今天先讲一个相对比较简单的情况——用一棵线段树维护主树每条边的权值。

 

二、概念

首先引入几个概念。

> 重儿子：设非叶子节点u存在若干个子节点，每个子节点有若干个子节点，重儿子即为其子节点中子节点最多的节点。

> 重边：非叶子节点与其重儿子所连的边。

> 重链：由连续的重边组成的一条链。

那么这些东西有什么用？先来看一道例题（也就是树链剖分与线段树维护的经典例题）。

 

三、例题

 

四、过程

　　题目为单点修改，区间询问。单点修改不用多提，重点在于，我们如何把从节点u到节点v这条路径上的节点求出最大值以及权值和呢？先考虑一种暴力的算法——跑LCA。我们根据u和v的深度找到公共父亲节点，然后在从子节点向上跳的时候，得到最大值或是权值和（如果是修改操作，其实也是同理）。然而这终究是暴力。那么，重链在这道题中的作用就凸显出来了——为了你在跑LCA的时候往上跳得更快。

　　根据最开始对重链等概念的描述，我们来看一张图：

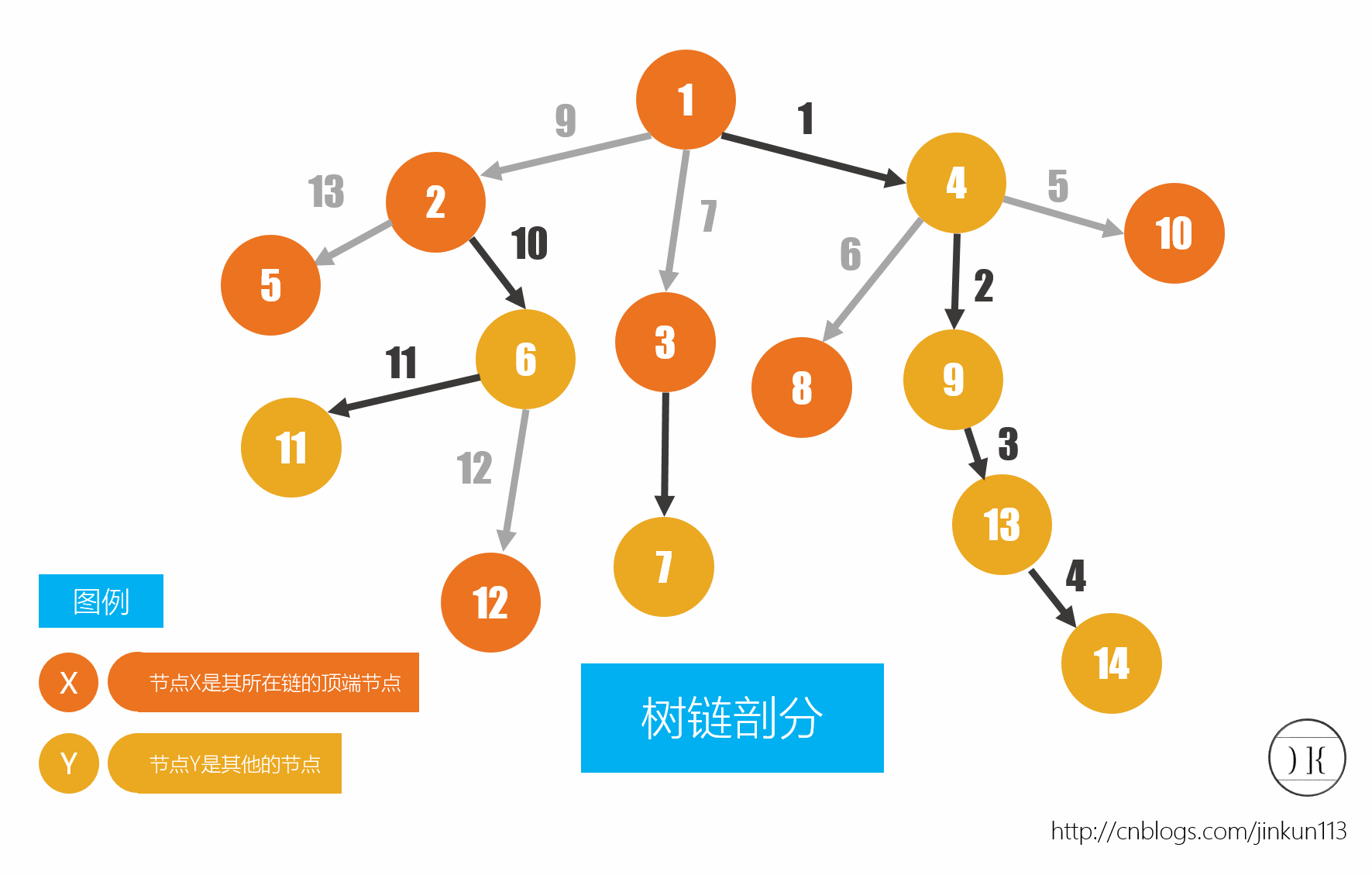
　　第一步，先求出每一个节点的重儿子，以及当前节点所在重链的顶端（如果当前节点是没有重边相连或者本身就是顶端，则就是其本身）。

　　第二步，根据重儿子，我们将每个节点对应的边标号（由于这是一棵树，则每一个节点与其父节点之间的边有且仅有一条，我们称之为节点对应的边）。编号时，优先为其重儿子编号，直到到了叶子节点，再回溯上去为其他的儿子编号。如图所示，最开始我们记根节点的重边为1，然后一路编下去直至14号节点，回溯到4号节点，将4号节点与另一个子节点的边标号为5，以此类推。

　　这样，我们的目的就开始显现了！一旦重链存在两条及以上的重边，其编号在线段树中一定是连续的。如图的1-2-3-4与10-11。

　　第三步，跑LCA。由于已经求出了每条重链的顶端，每次我们跑LCA的时候，若当前节点不是重链顶端，则可以直接跳到顶端——同时，因为他们在线段树的编号是连续的，所以可以很方便的进行求值或者是修改，这一点只要会线段树的就很好理解了！

　　举个例子，如果我们需要求出11号和10号点的路径上的权值之和，设初始状态x1=11,x2=10，步骤为：

　　1、11的顶端为2，修改线段树中的10-11，同时x1=2；这时，dep[x1]=2,dep[x2]=3；

　　2、10没有重边相连，顶端为自身，故向上找其父节点，修改线段树中的4；发现父节点所在重链顶端为1，则修改线段树中的1，同时x2=4；这时，dep[x1]=2,dep[x2]=1。（这里有一个小小的优化，即便这条链上是一条重边，一条轻边，也可以选择一次性向上跳完）

　　3、2没有重边相连，顶端为自身，故向上找其父节点，修改线段树中的9。此时，top[x1]=top[x2]，且x1=x2，循环结束。

 

五、代码

　　尽管个人认为整个过程已经描述的较为清楚，但代码实现起来依旧有很多需要注意的细节，原因在于树链剖分涉及面广，先进行的两遍DFS再加上后面的线段树操作，代码长，容易码错。这里对代码进行一些提示：

　　1、geth函数为第一次DFS，作用在于求出每一个节点的重儿子及其在树中的深度与其父节点；

　　2、mark函数为对每一条边进行标号，优先重边，同时维护好每一个节点与其对应边的关系；

　　3、qmax/qsum：本质为跑LCA，在深度不等的情况下，每次对深度较大的点向上找祖先，如果找到重链，则直接利用线段树维护的数据加快速度。

#include <cstdio>
#include <algorithm>
using namespace std;

#define MAXN 30005 
#define INF 0x3f3f3f3f

int n, q, u, v, o, w[MAXN], h[MAXN];
int f[MAXN], d[MAXN], tot[MAXN], hs[MAXN], top[MAXN], num[MAXN], lik[MAXN], now;
char ch[12];

struct Tree {
    int m, s;
} t[MAXN << 2];

struct Edge {
    int v, next;
} e[MAXN << 1];

void add(int u, int v) {
    o++, e[o] = (Edge) {v, h[u]}, h[u] = o;
    o++, e[o] = (Edge) {u, h[v]}, h[v] = o;
} 

int geth(int o, int of, int od) {
    int oh = -1;
    f[o] = of, d[o] = od;
    for (int x = h[o]; x; x = e[x].next) {
        int v = e[x].v;
        if (v == of) continue;
        tot[o] += geth(v, o, od + 1);
        if (tot[v] > oh) oh = tot[v], hs[o] = v;
    }
    return tot[o] + 1;
}

void mark(int o, int ot) {
    now++, top[o] = ot, num[o] = now, lik[now] = o;
    if (!hs[o]) return;
    mark(hs[o], ot);
    for (int x = h[o]; x; x = e[x].next) {
        int v = e[x].v;
        if (v != hs[o] && v != f[o]) mark(v, v); 
    }
}

void build(int o, int l, int r) {
    if (l == r) {
        t[o] = (Tree) {w[lik[l]], w[lik[l]]};
        return;
    }
    int m = (l + r) >> 1;
    build(o << 1, l, m), build(o << 1 | 1, m + 1, r);
    t[o] = (Tree) {max(t[o << 1].m, t[o << 1 | 1].m), t[o << 1].s + t[o << 1 | 1].s};
}    

void upd(int o, int l, int r, int x, int w) {
    if (l == r) {
        t[o].m += w, t[o].s += w;
        return;
    }
    int m = (l + r) >> 1;
    if (x <= m) upd(o << 1, l, m, x, w);
    else upd(o << 1 | 1, m + 1, r, x, w);
    t[o] = (Tree) {max(t[o << 1].m, t[o << 1 | 1].m), t[o << 1].s + t[o << 1 | 1].s};
}

int quem(int o, int l, int r, int ql, int qr) {
    int m = (l + r) >> 1, res = -INF;
    if (ql <= l && r <= qr) return t[o].m;
    if (ql <= m) res = max(res, quem(o << 1, l, m, ql, qr));
    if (qr > m) res = max(res, quem(o << 1 | 1, m + 1, r, ql, qr));
    return res;
}

int qmax() {
    int x = top[u], y = top[v], ans = -INF;
    while (x != y) {
        if (d[x] < d[y]) swap(x, y), swap(u, v);
        ans = max(ans, quem(1, 1, n, num[x], num[u]));
        u = f[x], x = top[u];
    }
    if (d[u] > d[v]) swap(u, v);
    return max(ans, quem(1, 1, n, num[u], num[v]));
}

int ques(int o, int l, int r, int ql, int qr) {
    int m = (l + r) >> 1, res = 0;
    if (ql <= l && r <= qr) return t[o].s;
    if (ql <= m) res += ques(o << 1, l, m, ql, qr);
    if (qr > m) res += ques(o << 1 | 1, m + 1, r, ql, qr);
    return res;
}

int qsum() {
    int x = top[u], y = top[v], ans = 0;
    while (x != y) {
        if (d[x] < d[y]) swap(x, y), swap(u, v);
        ans += ques(1, 1, n, num[x], num[u]);
        u = f[x], x = top[u];
    }
    if (d[u] > d[v]) swap(u, v);
    return ans + ques(1, 1, n, num[u], num[v]); 
}
 
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n - 1; i++) scanf("%d %d", &u, &v), add(u, v);
    for (int i = 1; i <= n; i++) scanf("%d", &w[i]);
    geth(1, 0, 1), mark(1, 1), build(1, 1, n);
    scanf("%d", &q);
    for (int i = 1; i <= q; i++) {
        scanf("%s %d %d", ch, &u, &v);
        if (ch[1] == 'H') upd(1, 1, n, num[u], v - w[u]), w[u] = v;
        else printf("%d\n", ch[1] == 'S' ? qsum() : qmax());
    } 
    return 0;
}