[知识点]Trie树和AC自动机

// 此博文为迁移而来，写于2015年5月27日，不代表本人现在的观点与看法。原始地址：http://blog.sina.com.cn/s/blog_6022c4720102w1s8.html

UPDATE（20180827）：代码重写。

 

一、前言

       因为Trie树和AC自动机的密切相关，我想一起讲完哈哈。。。看过前面博文的同学应该都知道了，AC自动机其实就是相当于在Trie树上跑KMP。

       

二、Trie树

       Trie树，就是字母树。Trie树是多叉树，每个节点为一个字母。其根节点为象征节点（就是说没有含义，但是存在这个节点），从根节点开始建立，每个节点至多为26个子节点，这样，我们就可以用这种方便快捷的方式存储字符串。其应用也不言而喻，用于保存，统计，排序，查找大量字符串。因为很简单，我们不讲太多，根据图像，自己造几个字符串，慢慢理解，看看代码，一下就懂了。

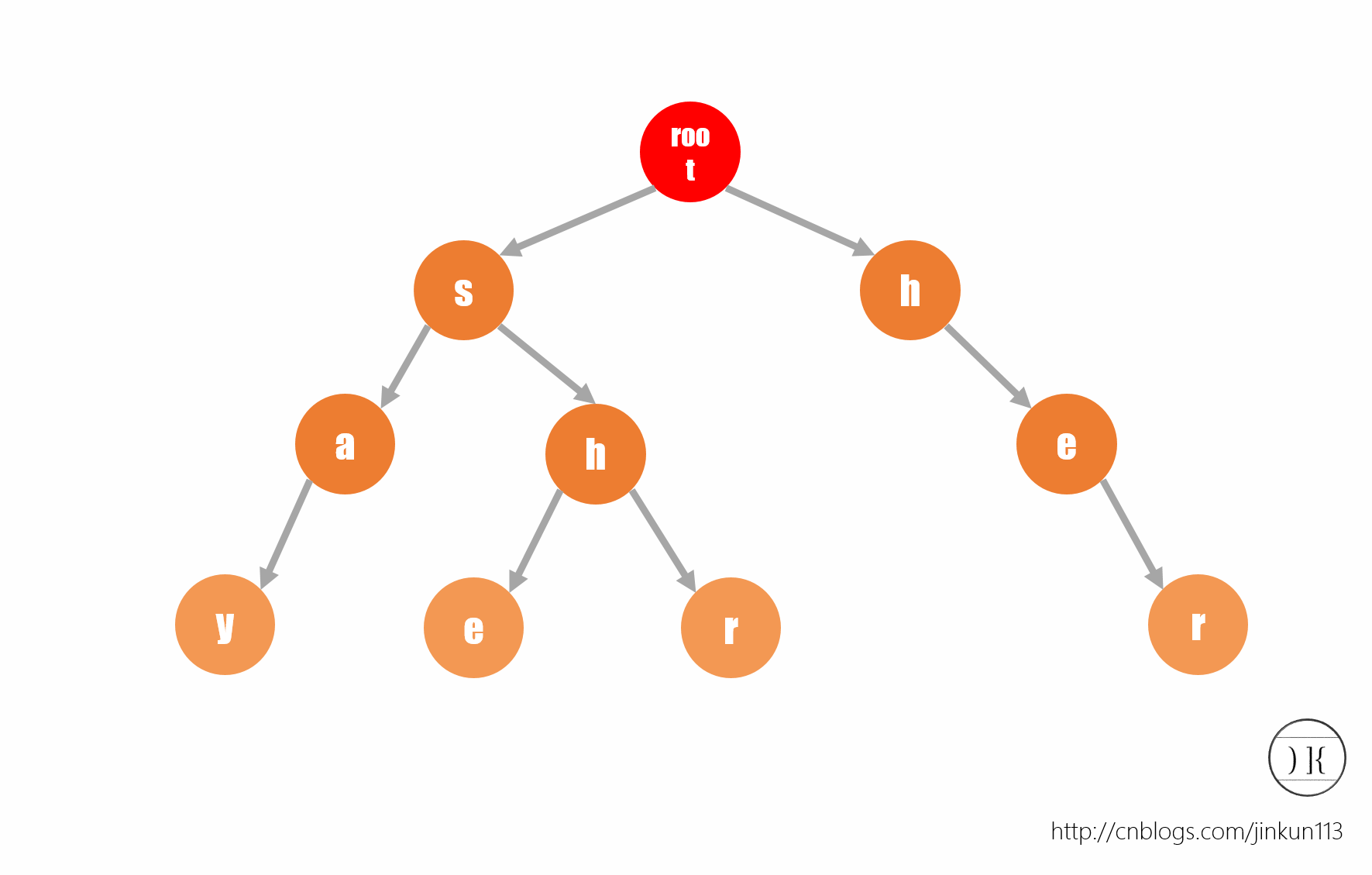
       如图所示，该字符串保存了say,she,shr,her四个字符串。有个小小的问题：在建树的时候，我们注意到最坏情况可能为二十六叉树，空间复杂度可想而知。所以，如果用指针能更省空间。

 

三、构造fail指针（KMP）

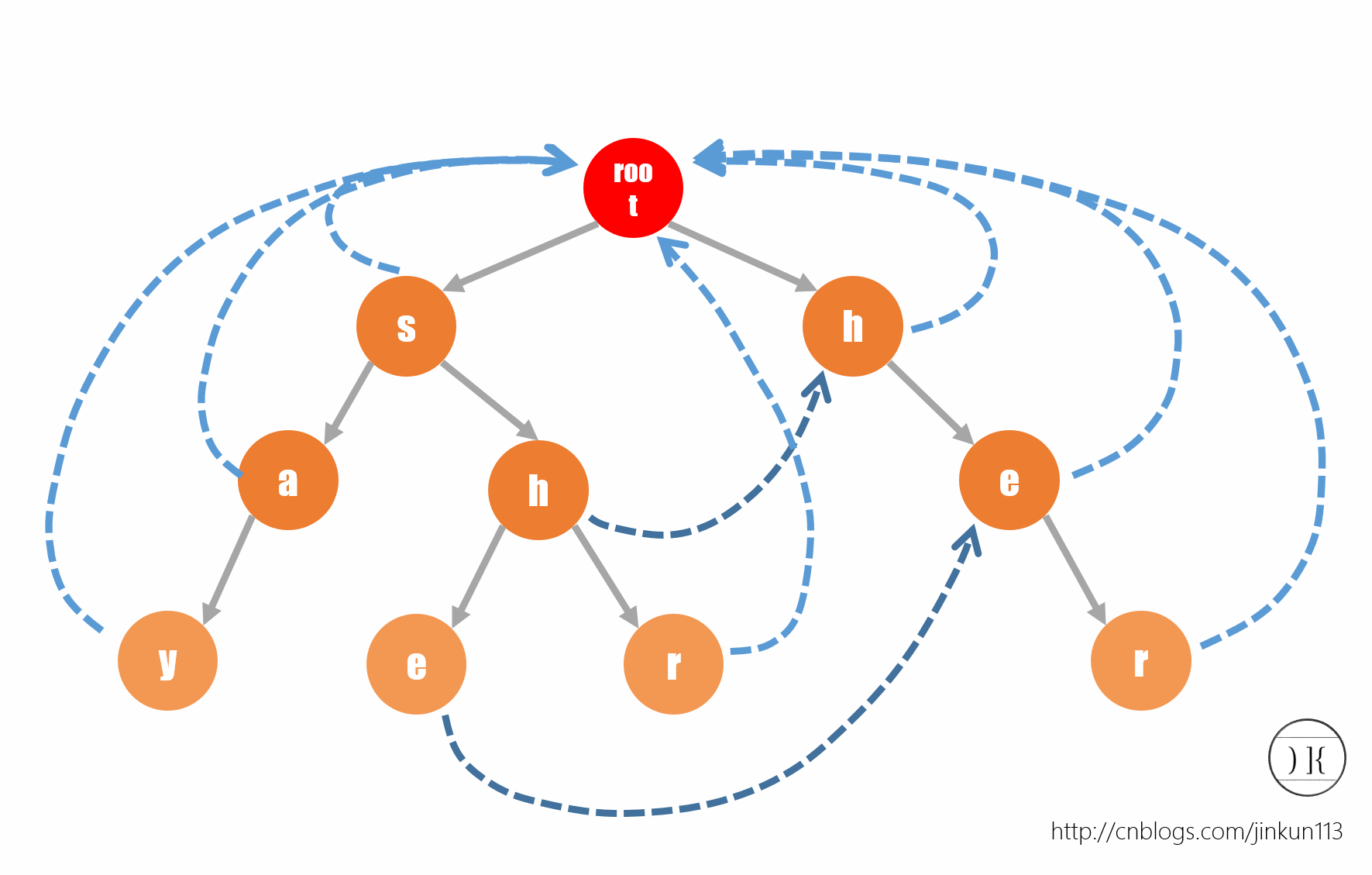
       在网上看到有许多AC自动机的算法分析，但是发现好像都很相似（莫非都是Ctrl+C/V）。构造fail指针，使当前字符失配时跳转到具有最长公共前后缀的字符继续匹配。如同 KMP算法一样， AC自动机在匹配时如果当前字符匹配失败，那么利用fail指针进行跳转。由此可知如果跳转，跳转后的串的前缀，必为跳转前的模式串的后缀。并且跳转的新位置的深度（匹配字符个数）一定小于跳之前的节点。

       我们在构建好Trie树之后，可以利用BFS进行 fail指针求解。我们最开始先将root节点入队，因为第一个字符不匹配需要重新匹配，所以第一个字符都指向root。这样，我们得到下图：

四、例题

 

Keywords Search [ HDU 2222 ]

       In the modern time, Search engine came into the life of everybody like Google, Baidu, etc.

Wiskey also wants to bring this feature to his image retrieval system.

       Every image have a long description, when users type some keywords to find the image, the system will match the keywords with description of image and show the image which the most keywords be matched.

      To simplify the problem, giving you a description of image, and some keywords, you should tell me how many keywords will be match. 

 

输入格式

       First line will contain one integer means how many cases will follow by.

       Each case will contain two integers N means the number of keywords and N keywords follow. (N <= 10000)

       Each keyword will only contains characters 'a'-'z', and the length will be not longer than 50.

       The last line is the description, and the length will be not longer than 1000000.

 

输出格式

       Print how many keywords are contained in the description.

 

输入样例

1

5

she

he

say

shr

her

yasherhs

 

输出样例

3

 

 

代码：

#include <cstdio>
#include <cstring>

#define MAXM 1000005

int T, n, tot, q[MAXM], ls, l, r;
char s[55], ch[MAXM];

struct Tree {
    int a[26], x, f;
} t[MAXM];

void insert() {
    int o = r;
    for (int i = 0; i < ls; i++) {
        int x = s[i] - 'a';
        if (!t[o].a[x]) t[o].a[x] = ++tot;
        o = t[o].a[x];
    }
    t[o].x++;
}

void getf() {
    int head = 1, tail = 2;
    q[1] = r;
    while (head != tail) {
        int o = q[head];
        for (int i = 0; i <= 25; i++) {
            int v = t[o].a[i];
            if (!v) continue;
            if (o == r) t[v].f = r;
            else {
                int of = t[o].f;
                while (of) {
                    if (t[of].a[i]) {
                        t[v].f = t[of].a[i];
                        break;
                    }
                    of = t[of].f;
                }
                if (!of) t[v].f = r;
            }
            q[tail++] = v; 
        }
        head++;
    }
}

int find() {
    int ans = 0, x = r;
    for (int i = 0; i < l; i++) {
        int o = ch[i] - 'a';
        while (!t[x].a[o] && x != r) x = t[x].f;
        x = t[x].a[o] ? t[x].a[o] : r;
        int y = x;
        while (t[y].x) ans += t[y].x, t[y].x = 0, y = t[y].f;
    }
    return ans;
}

int main() {
    scanf("%d", &T);
    for (int i = 1; i <= T; i++) {
        scanf("%d", &n), r = ++tot;
        for (int j = 1; j <= n; j++) scanf("%s", s), ls = strlen(s), insert();
        getf();
        for (int j = r + 1; j <= tot; j++) if (!t[j].f) t[j].f = r;
        scanf("%s", ch), l = strlen(ch);
        printf("%d\n", find());
    }
    return 0;
}