Dynamic Programming | Set 2 (Optimal Substructure Property)

正如我们在 Dynamic Programming | Set 1 (Overlapping Subproblems Property) 中讨论的那样，当一个问题具有以下2种性质时，建议使用动态规划来求解：

1 重叠子问题（Overlapping Subproblems）

2 最优子结构（Optimal Substructure）

我们已经在 Dynamic Programming | Set 1 (Overlapping Subproblems Property) 中讨论了重叠子问题，现在我们接着讨论最优子结构性质。

2 最优子结构（Optimal Substructure）

如果所求问题的最优解，可以通过其子问题的最优解获得，那么我们称该问题具有最优子结构性质。例如，最短路问题具有如下的最优子结构性质：如果节点x在源节点u到目标节点v的最短路径上，那么从u到v的最短路径，将由u到x的最短路径和x到v的最短路径组成。类似 Floyd–Warshall 以及 Bellman–Ford 的 standard All Pair Shortest Path algorithms 均是动态规划的典型例子。

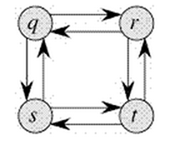
另一方面，最长路径问题不具备最优子结构性质。此处的最长路径指 longest simple path（path without cycle）。考虑如下的无权图：

从q到t有两条最长路径：q->r->t 以及 q->s->t。与最短路径不同的是，这些最长路径并不具备最优子结构性质。举例来说，q->r->t的最长路径，并非由q到r的最长路径和r到t的最长路径组合而得，因为从q到r的最长路径是q->s->t->r。