算法学习（一）

不论学习有多忙，也要抽空读点书。

算法

什么是算法？

有一个很著名的公式  “程序=数据结构+算法”。

曾经跟朋友吃饭的时候我问他什么是算法，他说算法嘛，就是一套方法，需要的时候拿过来，套用就可以，我吐槽他，他说的是小学数学题的算法，不是编程的算法。

算法，从字面意义上解释，就是用于计算的方法，通过该这种方法可以达到预期的计算结果。目前，被广泛认可的算法专业定义是：算法是模型分析的一组可行的，确定的，有穷的规则。通俗的说，算法也可以理解为一个解题步骤，有一些基本运算和规定的顺序构成。但是从计算机程序设计的角度看，算法由一系列求解问题的指令构成，能根据规范的输入，在有限的时间内获得有效的输出结果。算法代表了用系统的方法来描述解决问题的一种策略机制。

完成同一件事的不同的算法完成的时间和占用的资源可能并不相同，这就牵扯到效率的问题。算法的基本任务是针对一个具体的问题，找到一个高效的处理方法，从而完成任务。而这就是我们的责任了。

算法的五个特征：

一个典型的算法一般都可以抽象出5个特征：

有穷性：算法的指令或者步骤的执行次数和时间都是有限的。

确切性：算法的指令或步骤都有明确的定义。

输入：有相应的输入条件来刻画运算对象的初始情况。

输出：一个算应有明确的结果输出。

可行性：算法的执行步骤必须是可行的。

算法的分类：

根据应用分：

按照算法的应用领域，可以分为基本算法，数据结构相关算法，几何算法，图论算法，规划算法，数值分析算法，加密解密算法，排序算法，查找算法，并行算法，数值算法……

根据确定性分：

确定性算法：有限时间内完成，得到结果唯一。

非确定性算法：有限时间内完成，得到结果不唯一，存在多值性。

根据算法的思路分：

递推算法，递归算法，穷举算法，贪婪算法，分治算法，动态规划算法，迭代算法等。

算法和公式的关系

算法>=公式

如果没有接触到编程，的确很容易将算法理解为数学公式。公式的确具备算法的特征，但是算法并不等于公式，公式是一种高度精简的算法，算法的形式可以比公式更复杂，解决的问题更加广泛。

算法和程序的关系 程序也是算法的一种表现形式，也是一种工具

算法和数据结构的关系 

数据结构是数据的组织形式，可以用来表现特定的对象数据。

因为不同的数据结构所采用的处理方法不同，计算的复杂程度也不同，因此算法往往依赖于某种某种数据结构。数据结构是算法实现的基础。

算法的表示：

自然语言表示：

就是用我们的口头语言来表示算法，这样很多算法难以描述，不利于发展交流。

流程图表示：

一般有三种流程结构：

顺序结构，分支结构，循环结构

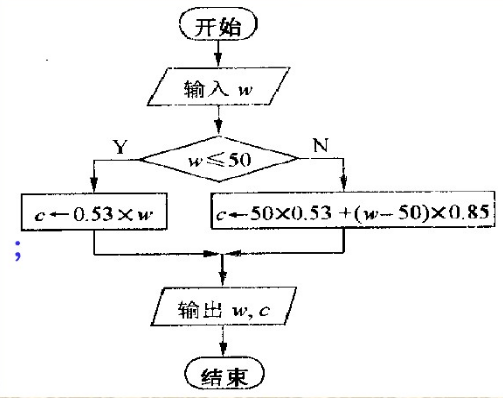
N-S图表示：

NS图也叫作盒图或者CHAPIN图，是用于取代传统流程图的一种描述方式。 以 SP方法为基础，NS图仅含有下图4.61 的5种基本成分，它们分别表示SP方法的几种标准控制结构。

伪代码表示：

伪代码并不是程序代码，伪代码介于自然语言和编程用语言之间，是将算法描述成类似编程语言的一种形式。

算法的性能评价

算法的效率作为判断算法优劣的标准。

一个算法的优劣往往通过算法复杂度来衡量，算法复杂度包括时间复杂度和空间复杂度两个方面。其作用：时间复杂度是指执行算法所需要的计算工作量；而空间复杂度是指执行这个算法所需要的内存空间。（算法的复杂性体现在运行该算法时的计算机所需资源的多少上，计算机资源最重要的是时间和空间（即寄存器）资源，因此复杂度分为时间和空间复杂度）。

时间复杂度

即通常所说的算法执行所需要耗费的时间，时间越短，算法越好。

计算方法

      1.一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n),使得当n趋近于无穷大时，T(n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n))，称O(f(n)) 为算法的渐进时间复杂度，简称时间复杂度。

      分析：随着模块n的增大，算法执行的时间的增长率和 f(n) 的增长率成正比，所以 f(n) 越小，算法的时间复杂度越低，算法的效率越高。

      2. 在计算时间复杂度的时候，先找出算法的基本操作，然后根据相应的各语句确定它的执行次数，再找出 T(n) 的同数量级（它的同数量级有以下：1，log2n，n，n log2n ，n的平方，n的三次方，2的n次方，n!），找出后，f(n) = 该数量级，若 T(n)/f(n) 求极限可得到一常数c，则时间复杂度T(n) = O(f(n))。

for(i=1; i<=n; ++i) { 

    for(j=1; j<=n; ++j) { 

        c[i][j] = 0;//该步骤属于基本操作执行次数：n的平方次 

        for(k=1; k<=n; ++k) 

            c[i][j] += a[i][k] * b[k][j];//该步骤属于基本操作执行次数：n的三次方次 

    } 

}    

      则有 T(n) = n 的平方+n的三次方，根据上面括号里的同数量级，我们可以确定 n的三次方 为T（n）的同数量级

      则有 f(n) = n的三次方，然后根据 T(n)/f(n) 求极限可得到常数c

      则该算法的时间复杂度：T(n) = O(n^3) 注：n^3即是n的3次方。

空间复杂度

空间复杂度可以分为两个方面：

1.程序保存所需要的存储空间，也就是程序的大小。

2.程序在执行过程中所需要消耗的存储空间资源，如程序在执行过程中的中间变量等。

简单算法实例：

随机生成一个20个整数数据的数组，然后输入要查找的数，然后用顺序查找法：

伪代码：

变量X<-输入待查找的数据

变量arr<-随机生成数据数组

 

for 1 to 20

　　if arr[i] ==x

　　　　break;找到数据

　　else

输出该数据的位置

程序结束

 

import java.util.Random;
import java.util.Scanner;

public class P1_1 {
    static int N=20;
    public static void main(String[] args) {
        int[] arr=new int[N];
        int x,n,i;
        int f=-1;

        Random r=new Random();                     //随机种子
        for(i=0;i<N;i++)
        {
            arr[i]=r.nextInt(100);                    //产生数组
        }
        
        System.out.print("随机生成的数据序列:\n");
        for(i=0;i<N;i++)
        {
            System.out.print(arr[i]+" ");                    //输出序列
        }
        System.out.print("\n\n");
            
        System.out.print("输入要查找的整数:");
        Scanner input=new Scanner(System.in);
        x=input.nextInt();                            //输入要查找的数

        for(i=0;i<N;i++)                            //顺序查找
        {
            if(x==arr[i])                            //找到数据
            {
                f=i;
                break;
            }
        }


        if(f<0)                                    //输出查找结果
        {
            System.out.println("没找到数据:"+x);
        }
        else
        {
            System.out.print("数据:"+x+" 位于数组的第 "+(f+1)+" 个元素处.\n");
        }
        
    }

}