topcoder srm 410 div1
problem1 link
不包含$gridConnections$ 的联通块一定是连在所有包含$gridConnections$的联通块中最大的那一块上。
import java.util.*;
import java.math.*;
import static java.lang.Math.*;
public class AddElectricalWires {
static class UnionSet {
public int[] father=null;
public int[] size=null;
public int[] edges=null;
public UnionSet(int n) {
father=new int[n];
size=new int[n];
edges=new int[n];
for(int i=0;i<n;++i) {
father[i]=i;
size[i]=1;
}
}
public int getFather(int x) {
if(father[x]==x) {
return x;
}
return father[x]=getFather(father[x]);
}
public UnionSet merge(int x,int y) {
int fx=getFather(x);
int fy=getFather(y);
if(fx!=fy) {
father[fx]=fy;
size[fy]+=size[fx];
edges[fy]+=edges[fx]+1;
}
else {
edges[fy]+=1;
}
return this;
}
}
public int maxNewWires(String[] wires,int[] gridConnections) {
final int n=wires.length;
UnionSet unionSet=new UnionSet(n);
for(int i=0;i<n;++i) {
for(int j=i+1;j<n;++j) {
if(wires[i].charAt(j)=='1') {
unionSet.merge(i,j);
}
}
}
int result=0;
long visited=0;
int maxSize=0;
for(int i=0;i<gridConnections.length;++i) {
int t=gridConnections[i];
int ft=unionSet.getFather(t);
int sz=unionSet.size[ft];
result+=sz*(sz-1)/2-unionSet.edges[ft];
visited|=1l<<ft;
if(sz>maxSize) {
maxSize=sz;
}
}
for(int i=0;i<n;++i) {
if(i==unionSet.getFather(i)&&(0==(visited&(1l<<i)))) {
int sz=unionSet.size[i];
result+=sz*(sz-1)/2-unionSet.edges[i];
result+=sz*maxSize;
maxSize+=sz;
}
}
return result;
}
}
problem2 link
每个$base$的选择一定是$addresses[i]$或者$addresses[i]-k+1$。这样进行动态规划即可。
import java.util.*;
import java.math.*;
import static java.lang.Math.*;
public class ContiguousCache {
public long minimumReads(int n, int k, int[] addresses) {
List<Integer> list=new ArrayList<>();
final int m=addresses.length;
for(int i=0;i<m;++i) {
final int t=addresses[i];
if(t-k+1>=0) {
list.add(t-k+1);
}
if(t<=n-k) {
list.add(t);
}
else {
list.add(n-k);
}
}
int[] a=unique(list);
final int p=a.length;
long[][] f=new long[m][p];
for(int i=0;i<m;++i) {
for(int j=0;j<p;++j) {
f[i][j]=-1;
}
}
for(int i=0;i<p;++i){
if(a[i]<=addresses[0]&&addresses[0]<a[i]+k) {
f[0][i]=Math.min(n,a[i]+k-1)-a[i]+1;
}
}
for(int i=1;i<m;++i) {
final int r=addresses[i];
for(int j=0;j<p;++j) {
if(f[i-1][j]==-1) {
continue;
}
for(int t=0;t<p;++t) {
if(a[t]<=r&&r<a[t]+k) {
long cost=f[i-1][j]+calCost(a[j],a[t],k);
if(f[i][t]==-1||f[i][t]>cost) {
f[i][t]=cost;
}
}
}
}
}
long result=-1;
for(int i=0;i<p;++i) {
if(f[m-1][i]==-1) {
continue;
}
if(result==-1||result>f[m-1][i]) {
result=f[m-1][i];
}
}
return result;
}
int calCost(int p1,int p2,int k) {
if(p1<p2) {
if(p1+k<=p2) {
return k;
}
return p2-p1;
}
else if(p1==p2) {
return 0;
}
else {
if(p2+k<=p1) {
return k;
}
return p1-p2;
}
}
int[] unique(List<Integer> list) {
Collections.sort(list);
int c=1;
int pre=0;
for(int i=1;i<list.size();++i) {
if(list.get(i)==list.get(pre)) {
continue;
}
++c;
pre=i;
}
int[] a=new int[c];
a[0]=list.get(0);
c=1;
for(int i=1;i<list.size();++i) {
if(a[c-1]!=list.get(i)) {
a[c++]=list.get(i);
}
}
return a;
}
}
problem3 link
首先进行梯形剖分。对于变形每条边$p,q$,分别向$x$轴做垂线,该边与垂线以及$x$轴可以组成一个梯形。对于$n$条边$n$个梯形来说,注意有的取正值有的取负值加起来就能得到整个内部的点个数。
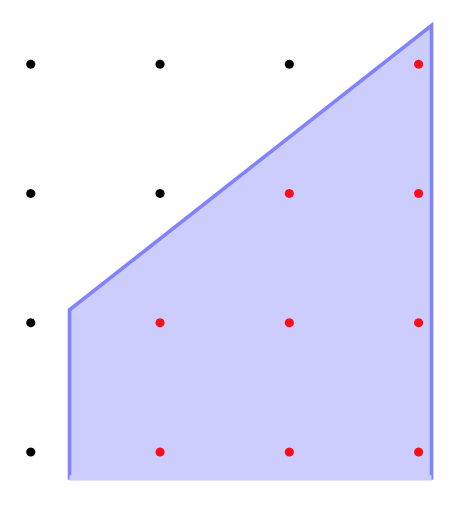
对于一个梯形来说,内部点可以用公式$\sum_{i=0}^{n-1}\left \lfloor \frac{a+di}{m} \right \rfloor$来进行计算。
这里可以认为$0\leq a < m,0<b<m$,否则可以直接提出到外面进行计算。
对于某个$i$,$\left \lfloor \frac{a+di}{m} \right \rfloor$的值可以看作垂线$(i,0),(i,a+di)$与水平线$y=km$的交点个数,$1\leq k \leq \left \lfloor \frac{a+di}{m} \right \rfloor$
到这里可以换个角度计算。对于每条水平线有多少垂线与其有交点。按照这个思路,可转化计算的公式:
$\sum_{i=0}^{n-1}\left \lfloor \frac{a+di}{m} \right \rfloor$=$\sum_{k=0}^{L-1}\left \lfloor \frac{(a+dn)mod(m)+mk}{d} \right \rfloor$,其中$L=\left \lfloor \frac{a+dn}{m} \right \rfloor$
中间的推导就不写了。
等号后面的式子跟前面形式类似,所以可以继续转化,每次求和项都在减少。
import java.util.*;
import java.math.*;
import static java.lang.Math.*;
public class WifiPlanet {
public long routersNeeded(int[] x, int[] y, int denom) {
final int n=x.length;
long result=0;
for(int i=0;i<n;++i) {
result+=cal(x[i],y[i],x[(i+1)%n],y[(i+1)%n],denom);
}
if(result<0) {
result=-result;
}
return result;
}
long cal(long x1,long y1,long x2,long y2,long m) {
if(x1==x2) {
return 0;
}
if(x1>x2) {
return -cal(x2,y2,x1,y1,m);
}
long L=(x1+m-1)/m*m;
long R=(x2-1)/m*m;
long n=(R-L)/m+1;
return dfs((y1*(x2-x1)+(y2-y1)*(L-x1))/m,y2-y1,n,x2-x1);
}
long dfs(long a,long d,long n,long m) {
if(n==0) {
return 0;
}
if(d==0) {
return a/m*n;
}
if(d<0) {
return dfs(a+d*(n-1),-d,n,m);
}
if(a>=m) {
return dfs(a%m,d,n,m)+a/m*n;
}
if(d>=m) {
return dfs(a,d%m,n,m)+(d/m)*n*(n-1)/2;
}
return dfs((a+n*d)%m,m,(a+n*d)/m,d);
}
}

