动态规划完整笔记

动态规划的实质： 根据小问题的结果来判断大问题的结果

  • 记忆化搜索
  • 避免中间重复的计算结果

什么时候使用动态规划：

  • 求最大最小值
  • 判断是否可行
  • 统计方案个数

什么时候不用动态规划：

  • 求出所有具体的方案而非方案个数
  • 输入数据是一个集合而不是序列
  • 暴力算法的复杂度已经是多项式级别
    1. 动态规划擅长优化指数级别复杂度（2^n, n!）到多项式级别复杂度（n^2, n^3）
    2. 不擅长优化n^3到n^2

动态规划4要素 

  1. 状态 存储小规模问题的结果
  2. 方程 状态之间的联系，怎么通过小的状态来算大的状态
  3. 初始化 最极限的小状态是什么，起点
  4. 答案  最大的那个状态是什么，终点

 

 

面试中动态规划类型：

1. 坐标型动态规划

　　state:  

　　　　f[x]表示我从起点走到坐标x....

　　　　f[x][y] 表示我从起点走到坐标x,y....

　　function: 研究走到x,y这个点之前的一步

　　initialize: 起点

　　answer：终点

 

 

　　1.1 Minimum Path Sum 

　　Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.

 1 public class Solution {
 2     public int minPathSum(int[][] grid) {
 3         if (grid == null || grid.length == 0 || grid[0].length == 0) {
 4             return 0;
 5         }
 6         
 7         //initialize 
 8         int m = grid.length;
 9         int n = grid[0].length;        
10         int[][] sum = new int[m][n];
11         sum[0][0] = grid[0][0];
12         
13         for (int i = 1; i < m; i++) {
14             sum[i][0] = grid[i][0] + sum[i - 1][0];
15         }
16         
17         for (int i = 1; i < n; i++) {
18             sum[0][i] = grid[0][i] + sum[0][i - 1];
19         }
20         
21         //dp
22         for (int i = 1; i < m; i++) {
23             for (int j = 1; j < n; j++) {
24                 sum[i][j] = grid[i][j] + Math.min(sum[i - 1][j] , sum[i][j - 1]);
25             }
26         }
27         return sum[m - 1][n -1];
28     }
29 }
Minimum Path Sum

　　注意： 对于二维数组的判断，  a == NULL ||  a.length == 0 || a[0].length == 0

　　state: f[x][y] 从起点走到x，y的最小路径

　　function: f[x][y] = min(f[x - 1][y], f[x][y - 1]) + A[x][y];

　　initialize: f[i][0] = sum(0,0~i,0)

　　　　　　　f[0][i] = sum(0,0~0,i)

　　answer: f[m - 1][n - 1]  

　　记住： 初始化一个二位的动态规划时，就去初始化第0行和第0列

　

　　1.2 Unique Paths　

　　

　　A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

 

　　The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 　　'Finish' in the diagram below).

 

　　How many possible unique paths are there?

 

　　

 1 public class Solution {
 2     public int uniquePaths(int m, int n) {
 3         if (m == 0 || n == 0) {
 4             return 0;
 5         }
 6         
 7         int[][] sum = new int[m][n];
 8         for (int i = 0; i < m; i++) {
 9             sum[i][0] = 1;
10         }
11         for (int i = 0; i < n; i++) {
12             sum[0][i] = 1;
13         }
14         for (int i = 1; i < m; i++) {
15             for (int j = 1; j < n; j++) {
16                 sum[i][j] = sum[i - 1][j] + sum[i][j - 1];
17             }
18         }
19         return sum[m - 1][n - 1];
20     }
21 }
unique paths

　　state: f[x][y] 表示从起点到(x,y)的路径数

　　function: f[x][y] = f[x - 1][y] + f[x][y - 1]

　　initialize: f[0][i] = 1;    f[i][0] = 1;

　　answer: f[m - 1][n - 1]　　　　　　　

 

　　1.3 Jump Game

　　最优算法：贪心法 时间复杂度为o(n)

　　次优算法：动态规划，时间复杂度为o(n^2)

 

 1 public class Solution {
 2     public boolean canJump(int[] A) {
 3         // think it as merging n intervals
 4         if (A == null || A.length == 0) {
 5             return false;
 6         }
 7         int farthest = A[0];
 8         for (int i = 1; i < A.length; i++) {
 9             if (i <= farthest && A[i] + i >= farthest) {
10                 farthest = A[i] + i;
11             }
12         }
13         return farthest >= A.length - 1;
14     }
15 }
jump game greedy

 

 1 public class Solution {
 2     public boolean canJump(int[] nums) {
 3         // 会超时
 4         int length = nums.length;
 5         boolean[] canJump = new boolean[length];
 6         canJump[0] = true;
 7         
 8         
 9         for (int i = 1; i < length; i++) {
10             for (int j = 0 ; j < i; j++) {
11                 if (canJump[j] && j + nums[j] >= i) {
12                     canJump[i] = true;
13                     break;
14                 }
15             }
16         }
17         return canJump[length - 1];
18     }
19 }
jump game DP

 

　　1.4 Jump Game 2

　　最优算法：贪心法 时间复杂度为o(n)

　　次优算法：动态规划，时间复杂度为o(n^2)

　　

 1 public class Solution {
 2     public int jump(int[] A) {
 3         int[] steps = new int[A.length];
 4         
 5         steps[0] = 0;
 6         for (int i = 1; i < A.length; i++) {
 7             steps[i] = Integer.MAX_VALUE;
 8             for (int j = 0; j < i; j++) {
 9                 if (steps[j] != Integer.MAX_VALUE && j + A[j] >= i) {
10                     steps[i] = steps[j] + 1;
11                     break;
12                 }
13             }
14         }
15         
16         return steps[A.length - 1];
17     }
18 }
jump game 2 DP

 

 1 public class Solution {
 2     public int jump(int[] nums) {
 3         int minStep = 0;
 4         int maxDis = 0;
 5         int last = 0;
 6         for (int i = 0; i < nums.length; i++) {
 7             if (i > last) {
 8                 last = maxDis;
 9                 minStep++;
10             }
11             maxDis = Math.max(maxDis, nums[i] + i);
12         }
13         return minStep;
14     }
15 }
Jump game 2

　　greedy 方法的核心思想是

　　3个变量   1. 当前第几次跳   2 扫描到当前点并且在这次跳范围内能达到的最远距离    3 整体的能达到的最远距离

　　扫一遍数组，找到第x次能跳的最大距离，  1. 第x＋1个点 如果超出当前跳能达到的距离，那么更新跳的次数

　　　　　　　　　　　　　　　　　　　　　2. 第x＋1个点 如果没超出当前能达到的距离（即当前点也是当前次数能跳到的），那么比较i＋a［i］和currentMax的

　　大小，看看是否需要更新局部的最远距离。

　　做一次新的跳跃后，把局部的最远距离赋值给整体的最远距离。

　　总之做法很牛逼。。。。

　　1.5 Longest Increasing Subsequence

 1 public class Solution {
 2     public int lengthOfLIS(int[] nums) {
 3         if (nums == null || nums.length == 0) {
 4             return 0;
 5         }
 6         int[] minNum = new int[nums.length];
 7         minNum[0] = 0;
 8         int max = 0;
 9         for (int i = 1; i < nums.length; i++) {
10             int j = i - 1;
11             while (j >= 0) {
12                 if (nums[i] > nums[j]) {
13                     minNum[i] = Math.max(minNum[j] + 1, minNum[i]);
14                 }
15                 j--;
16             }
17         }
18         Arrays.sort(minNum);
19         return minNum[nums.length - 1] + 1;
20     }
21 }
View Code

　　1.6 Maximal Square

　　二维坐标型动态规划

　　思路： 分析大问题的结果与小问题的相关性 f[i][j] 表示以i和j作为正方形的右下角可以扩展的最大边长

　　eg： 1  1  1

　　　　 1  1  1

　　　　 1  1   1(traget)

　　　　traget 的值与3部分相关  1. 青色的正方形部分 f[i - 1][j - 1]

　　　　　　　　　　　　　　　  2. 紫色 target上面的数组 up[i][j - 1]即target上面的点 往上延伸能达到的最大长度

　　　　　　　　　　　　　　　  3. 橙色的target左边的数组 left[i - 1][j]

　　　　如果 target ＝＝ 1

 　　　　　　f[i][j] = min (left[i - 1][j], up[i][j - 1], f[i - 1][j - 1]) + 1;

　　　　对于left和up数组 可以在intialization的时候用o(n^2)扫描整个图形实现！

　　优化思路1:

　　因为

　　　　　　f[i - 1][j] = left[i - 1][j]

　　　　　　f[i][j - 1] = up[i][j - 1]

　　这样 不需要额外的建立left和up数组

　　　　if (target == 1)　　

　　　　f[i][j] = min (f[i - 1][j - 1], f[i][j - 1],f[i - 1][j]) + 1;

　　优化思路2:

　　由于f[i][j]只和前3个结果相关

　　　f[i - 1][j - 1]    f[i][j - 1]

　　　f[i - 1][j]         f[i][j]　　

　　故只需要保留一个2行的数组！！！

　　列上不能优化，因为2重循环的时候 下列的时候依赖于上列的结果，上列的结果需要保存到计算下列的时候用。

　　只能在行上滚动，不能行列同时滚动！！！

　　－－－－－－－－－－－－－－－－－－－－

　　state： f[i][j] 表示以i和j作为正方形右下角可以扩展的最大边长

　　function: 

　　　　if matrix[i][j] == 1

　　　　　　f[i % 2][j] = min(f[(i - 1) % 2 ][j], f[(i - 1) % 2][j - 1], f[i％2][j - 1]) + 1;

　　initialization:

　　　　f[i%2][0] = matrix[i][0]

　　　　f[0][j] = matrix[0][j]

　　answer:

　　　　max{f[i%2][j]}

 

 1 public class Solution {
 2     public int maximalSquare(char[][] matrix) {
 3         
 4         int result = 0;
 5         int m = matrix.length;
 6         if (m == 0) {
 7             return 0;
 8         }
 9         
10         int n = matrix[0].length;
11         int[][] dp = new int[2][n];
12         for (int i = 0; i < n; i++) {
13             dp[0][i] = matrix[0][i] - '0';
14             result = Math.max(dp[0][i], result);
15         }
16         
17         for (int i = 1; i < m; i++) {
18             dp[i % 2][0] = matrix[i][0] - '0';
19             for (int j = 1; j < n; j++) {
20                 if (matrix[i][j] == '1') {
21                     dp[i % 2][j] = Math.min(dp[(i - 1) % 2][j],Math.min(dp[(i - 1) % 2][j - 1], dp[i % 2][j - 1])) + 1;
22                     result = Math.max(dp[i % 2][j], result);
23                 } else {
24                     dp[i % 2][j] = 0;
25                 }
26             }
27         }
28         
29         return result * result;
30         
31     }
32 }
maximal square

 

　　

2. 序列型动态规划

　　state: f[i]表示前i个位置／数字／字符， 第i个...

　　function: f[i] = f[j]...  j是i之前的一个位置

　　initialize: f[0]...

　　answer: f[n]...

　　一般answer是f(n)而不是f(n - 1)   因为对于n个最富，包含前0个字符(空串)，前1个字符...前n个字符。

　　注意： 如果不是跟坐标相关的动态规划，一般有n个数／字符，就开n＋1个位置的数组。 第0个位置单独留出来作初始化

　　2.1 word break 

 1 public class Solution {
 2     public boolean wordBreak(String s, Set<String> wordDict) {
 3         boolean canBreak[] = new boolean[s.length() + 1];
 4         canBreak[0] = true;
 5         for (int i = 1; i < s.length() + 1; i++) {
 6             for (int j = 0; j < i; j++) {
 7                 if (canBreak[j] == true && wordDict.contains(s.substring(j, i))) {
 8                     canBreak[i] = true;
 9                     break;
10                 }
11             }
12         }
13         return canBreak[s.length()];
14     }
15 }
word break

　　2.2 word break ii

　　难到爆炸 但是总体上是熟悉的套路！

 1 public class Solution {
 2     public List<String> wordBreak(String s, Set<String> wordDict) {
 3         ArrayList<String> result = new ArrayList<String>();
 4         if (s == null || s.length() == 0) {
 5             return result; 
 6         }
 7         
 8         //坐标型动态规划！ o(n^2) 
 9         // provide o(1) complexity to tell a whether a string is a word
10         boolean[][] isWord = new boolean[s.length()][s.length()];
11         for (int i = 0; i < s.length(); i++) {
12             for (int j = i; j < s.length(); j++) {
13                 if (wordDict.contains(s.substring(i,j + 1))) {
14                     isWord[i][j] = true;
15                 }
16             }
17         }
18        
19         //单序列型动态规划！
20         //检测从i位置出发 是否能达到末尾位置
21         boolean[] possible = new boolean[s.length() + 1];
22         possible[s.length()] = true;
23         for (int i = s.length() - 1; i >= 0; i--) {
24             for (int j = i; j < s.length(); j++) {
25                 if (isWord[i][j] && possible[j + 1]) {
26                     possible[i] = true;
27                     break;
28                 }
29             }
30         }
31         List<Integer> path = new ArrayList<Integer>();
32         search(0, s, path, isWord, possible, result);
33         return result;
34     }
35     
36       private void search(int index, String s, List<Integer> path,
37                    boolean[][] isWord, boolean[] possible,
38                    List<String> result) {
39                        
40         //从index点不能走到末尾 故不需要考虑从index点开始的情况               
41         if (!possible[index]) {
42             return;
43         }
44         
45         //index 走到末尾了，path里存的断点坐标转换为string
46         if (index == s.length()) {
47             StringBuilder sb = new StringBuilder();
48             int lastIndex = 0;
49             for (int i = 0; i < path.size(); i++) {
50                 sb.append(s.substring(lastIndex, path.get(i)));
51                 if (i != path.size() - 1) sb.append(" ");
52                 lastIndex = path.get(i);
53             }
54             result.add(sb.toString());
55             return;
56         }
57         
58         //递归计算从index点出发的路径 类似于travse a binary tree的方式
59         for (int i = index; i < s.length(); i++) {
60             if (!isWord[index][i]) {
61                 continue;
62             }
63             path.add(i + 1);
64             search(i + 1, s, path, isWord, possible, result);
65             path.remove(path.size() - 1);
66         }
67     }
68 }
word break ii

　　

　　2.3 House Robber

　　很简单的一道单序列动态规划问题 f[i]的状态只与f[i - 1]和f［i - 2] 相关

　　state: f[i]

　　function：max(f[i - 1], f[i - 2] + A[i - 1])

　　initialize: f[0] = 0; 当没有house可以抢的时候为0

　　　　　　　f[1] = A[0];  当只有1个house的时候，为house的当前值

　　answer： f[size]

　　

 1 public class Solution {
 2     /**
 3      * @param A: An array of non-negative integers.
 4      * return: The maximum amount of money you can rob tonight
 5      */
 6     public long houseRobber(int[] A) {
 7         // write your code here
 8         if (A == null || A.length == 0) {
 9             return 0;
10         }   
11         int size = A.length;
12         long[] dp = new long[size + 1];
13         dp[0] = 0;
14         dp[1] = A[0];
15         for (int i = 2; i <= size; i++) {
16             dp[i] = Math.max(dp[i - 1], dp[i - 2] + A[i - 1]);
17         }
18         return dp[size];
19     }
20 }
View Code

　　滚动数组优化：由于f[i]的状态只与前2个状态有关，那么其实只用记录2个状态量，利用滚动数组把o(n) 优化为o(1)

　　注意：滚动数组的size取决于　 function里面 大问题的答案来自于几个小问题　　

　　function：max(f[i - 1], f[i - 2] + A[i - 1])  转化为：

　　　　　　　f[i%2] = max(f[(i - 1)%2], (f[(i - 2)%2]+ a[i - 1]))  note: 新得到的值覆盖掉旧数组里的对应的值

　　　　　　　观察我们要保留的状态来确定模数

　　house robber version2

　　state: f[i] 表示前i个房子中，偷到的最大价值

　　function: f[i%2] = max(f[(i - 1) % 2], (f[(i - 2) % 2] + a[i - 1]));

　　initialize: f[0] = 0; 

　　　　　　　f[1] = A[0]; 

　　

 1 public class Solution {
 2     public int rob(int[] nums) {
 3         //version 2 optimize with 滚动数组
 4         if (nums == null || nums.length == 0) {
 5             return 0;
 6         }   
 7         int size = nums.length;
 8         int[] dp = new int[2];
 9         dp[0] = 0;
10         dp[1] = nums[0];
11         for (int i = 2; i <= size; i++) {
12             dp[i%2] = Math.max(dp[(i - 1) % 2], dp[(i - 2) % 2] + nums[i - 1]);
13         }
14         return dp[size % 2];
15     }
16 }
house robber version2

　　2.4 House Robber ii

　　After robbing those houses on that street, the thief has found himself a new place for his thievery so that he will not get too much attention. This 　　time, all houses at this place are arranged in a circle. That means the first house is the neighbor of the last one. Meanwhile, the security 　　system for these houses remain the same as for those in the previous street.

　　Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob 　　tonightwithout alerting the police.

 　　　即首尾点不能同时取

　　　思路，把第一个点放在尾巴处，如果没有取到尾点，那么再做一次比较，看看是否加入首点。 ❌ 因为是否放入首点，除了考虑是否放入末尾节点外还要考虑是否放入了第二个点。

　　　正确的思路：区分加不加首点，直接2种情况下分别做动态规划！

　　　在不同情况下，分情况做多次dp或者其他算法，不会影响整体的时间复杂度，分情况套用一个helper function！　　　

 1 public class Solution {
 2     /**
 3      * @param nums: An array of non-negative integers.
 4      * return: The maximum amount of money you can rob tonight
 5      */
 6     public int houseRobber2(int[] nums) {
 7         // write your code here
 8         if (nums == null || nums.length == 0) {
 9             return 0;
10         }
11         int size = nums.length;
12         if (size == 1) {
13             return nums[0];
14         }
15         return Math.max(helper(nums, 0 , size - 1), helper(nums, 1, size));
16     }
17     private int helper(int[] nums, int start, int end) {
18         int[] dp = new int[2];
19         dp[0] = 0;
20         dp[1] = nums[start];
21         int size = end - start;
22         for (int i = 2; i <= size; i++) {
23             dp[i % 2] = Math.max(dp[(i - 1) % 2], (dp[(i - 2) % 2] + nums[i - 1 + start]));
24         }
25         return dp[size % 2];
26     }
27 }
House Robber ii

 

　　

　　2.5 House Robber iii

　　这道题很重要的在于理解对于当前node的结果 来自于本层当前的child和grandchild的结果。故依赖于前2层的结果，还是需要利用滚动数组做动态规划！

//dp[i][0]表示以i为根的子树不偷根节点能获得的最高价值，dp[i][1]表示以i为根的子树偷根节点能获得的最高价值

　　理解这个长度为2的数组是如何在递归的时候变化的！ 

 1 /**
 2  * Definition for a binary tree node.
 3  * public class TreeNode {
 4  *     int val;
 5  *     TreeNode left;
 6  *     TreeNode right;
 7  *     TreeNode(int x) { val = x; }
 8  * }
 9  */
10 public class Solution {
11     public int rob(TreeNode root) {
12         if (root == null) {
13             return 0;
14         }
15         int[] result = helper(root);
16         return Math.max(result[0], result[1]);
17     }
18     
19     private int[] helper(TreeNode node) {
20         if (node == null) {
21             return new int[]{0,0};
22         }
23         
24         int[] left = helper(node.left);
25         int[] right = helper(node.right);
26         int[] now = new int[2];
27         now[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
28         now[1] = left[0] + right[0] + node.val;
29 
30         return now;
31     }
32 }
View Code

　

　　2.6 Decode ways

　　典型的序列型动态规划，记住，开n＋1个位置，从空串的位置开始 很重要！！！

　　空串的初始化，应该为1而不是0，因为空串也作为一个合理的decode方式。 

　　注意，dp[i]的状态依赖于dp[i - 1] 和 dp[i - 2]

　　dp[i]是2者的累加和，所以分别考虑是否需要添加该部分

 1 public class Solution {
 2     public int numDecodings(String s) {
 3         if (s == null || s.length() == 0) {
 4             return s.length();
 5         }
 6         int m = s.length();
 7         int[] dp = new int[m + 1];
 8         dp[0] = 1;//犯错点： 作为前面的空串也认为是1种解析方式 eg： 空串＋10 就是dp［2］ ＝ dp［0］ ＝ 1
 9         dp[1] = s.charAt(0) == '0' ? 0 : 1;
10         for (int i = 2; i <= m; i++) {
11             //分2种情况
12             int temp1 = s.charAt(i - 2) -'0';
13             int temp2 = s.charAt(i - 1) - '0';
14             // 1. 1个digits单独作为一个数
15             if(temp2 > 0) {
16                 dp[i] = dp[i - 1];
17             } 
18             
19             //2. 2个digits作为1个数
20             int twodigits = temp1 * 10 + temp2;
21             if(twodigits >= 10 && twodigits <= 26) {
22                 dp[i] += dp[i - 2];
23             }
24         }
25         return dp[m];
26     }
27 }
91. Decode Ways

　　2.7 Coin Change

　　dp[i] : 表示组成面值i所需的最小的coin个数。

　　注意，面值为0 的时候，直接返回0

　　　　先把所有的dp[i]都变成max的int

　　　　返回的时候，如果dp[k] = Math.MAX_VALUE， 那么返回－1， 这个需要最后单独做处理

 1 public class Solution {
 2     public int coinChange(int[] coins, int amount) {
 3         if (amount == 0) return 0;
 4         int[] dp = new int[amount + 1];
 5         dp[0] = 0;
 6         int size = coins.length;
 7         for (int i = 1; i <= amount; i++) {
 8             dp[i] = Integer.MAX_VALUE;
 9             for (int value : coins) {
10                 if (i >= value && dp[i - value] != Integer.MAX_VALUE) {
11                     dp[i] = Math.min(dp[i - value] + 1, dp[i]);
12                 }
13             }
14         }
15          
16          
17          if(dp[amount] < Integer.MAX_VALUE && dp[amount] > 0) {
18             return dp[amount];
19         } else {
20             return -1;
21         }  
22             
23     }
24 }
View Code

 

　　2.8 Integer break 

Given a positive integer n, break it into the sum of at least two positive integers and maximize the product of those integers. Return the maximum product you can get.

For example, given n = 2, return 1 (2 = 1 + 1); given n = 10, return 36 (10 = 3 + 3 + 4).

Note: you may assume that n is not less than 2.

Hint:

  1. There is a simple O(n) solution to this problem.
  2. You may check the breaking results of n ranging from 7 to 10 to discover the regularities.

 

 

这道题给了我们一个正整数n，让我们拆分成至少两个正整数之和，使其乘积最大，题目提示中让我们用O(n)来解题，而且告诉我们找7到10之间的规律，那么我们一点一点的来分析：

正整数从1开始，但是1不能拆分成两个正整数之和，所以不能当输出。

那么2只能拆成1+1，所以乘积也为1。

数字3可以拆分成2+1或1+1+1，显然第一种拆分方法乘积大为2。

数字4拆成2+2，乘积最大，为4。

数字5拆成3+2，乘积最大，为6。

数字6拆成3+3，乘积最大，为9。

数字7拆为3+4，乘积最大，为12。

数字8拆为3+3+2，乘积最大，为18。

数字9拆为3+3+3，乘积最大，为27。

数字10拆为3+3+4，乘积最大，为36。

 

 1 public class Solution {
 2     public int integerBreak(int n) {
 3         if (n == 2 || n == 3) {
 4             return n - 1;
 5         }
 6         int res = 1;
 7         while (n > 4) {
 8             n = n - 3;
 9             res = res* 3;
10         }
11         return res*n;
12     }
13 }
Integer Break

 

我们再来观察上面列出的10之前数字的规律，我们还可以发现数字7拆分结果是数字4的三倍，而7比4正好大三，数字8拆分结果是数字5的三倍，而8比5大3，后面都是这样的规律，那么我们可以把数字6之前的拆分结果都列举出来，然后之后的数通过查表都能计算出来，参见代码如下；

 1 public class Solution {
 2     public int integerBreak(int n) {
 3         int[] dp = new int[]{0, 0, 1, 2, 4, 6, 9};
 4         
 5 
 6         int res = 1;
 7         while (n > 6) {
 8             n = n - 3;
 9             res = res* 3;
10         }
11         return res * dp[n];
12     }
13 }
View Code

 



3. 双序列动态规划

　　state: f[i][j]代表了第一个sequence的前i个数字／字符，配上第二个sequence的前j个...

　　function: f[i][j] = 研究第i个和第j个的匹配关系

　　initialize: f[i][0] 和f[0][i]

　　answer: f[n][m]

　　n = s1.length(); m = s2.length()

　　3.1 Longest Common Subsequence

　　LCS经典问题

　　state：f[i][j] 表示第一个字符串的前i个字符配上第二个字符串的前j个字符的LCS长度

　　function：注意研究的是第i个字符和第j个字符的关系 a[i - 1] 与 b［j - 1］的关系

　　　　　　　　if (a[i - 1] == b[j - 1]) {

　　　　　　　　　　f[i][j] = f[i - 1][j - 1] + 1;

　　　　　　　　} else {

　　　　　　　　　　f[i][j] = Math.max(f[i - 1][j], f[i][j - 1]);

　　　　　　　　}

　　initialize：f[i][0] = 0; f[0][j] = 0;

　　answer：f[n][m];

　　

 1 public class Solution {
 2     /**
 3      * @param A, B: Two strings.
 4      * @return: The length of longest common subsequence of A and B.
 5      */
 6     public int longestCommonSubsequence(String A, String B) {
 7         // write your code here
 8         if (A == null || B == null) {
 9             return 0;
10         }
11         
12         int m = A.length();
13         int n = B.length();
14         if (m == 0 || n == 0) {
15             return 0;
16         }
17         int[][] lcs = new int[m + 1][n + 1];
18         for (int i = 0; i <= m; i++) {
19             lcs[i][0] = 0;
20         }
21         for (int i = 0; i <= n; i++) {
22             lcs[0][i] = 0;
23         }
24         
25         for (int i = 1; i <=m; i++) {
26             for (int j = 1; j <= n; j++) {
27                 if (A.charAt(i - 1) == B.charAt(j - 1)) {
28                     lcs[i][j] = lcs[i - 1][j - 1] + 1;
29                 } else {
30                     lcs[i][j] = Math.max(lcs[i - 1][j], lcs[i][j - 1]);
31                 }
32             }
33         }
34         return lcs[m][n];
35     }
36 }
Longest common Subsequence

　　

　　类似问题： 比较当前的char是否相同 Longest Common Substring

　　 很巧妙的在while循环里利用 i＋len 作为控制条件！

　　

 1 public class Solution {
 2     /**
 3      * @param A, B: Two string.
 4      * @return: the length of the longest common substring.
 5      */
 6     public int longestCommonSubstring(String A, String B) {
 7         // write your code here
 8         if (A == null || B == null) {
 9             return 0;
10         }
11         
12         int maxLen = 0;
13         int m = A.length();
14         int n = B.length();
15         if (m == 0 || n == 0) {
16             return 0;
17         }
18         
19         for (int i = 0; i < m; i++) {
20             for (int j = 0; j < n; j++) {
21                 int len = 0;
22                 while (i + len < m && j + len < n &&
23                     A.charAt(i + len) == B.charAt(j + len)){
24                     len++;
25                     if(len > maxLen)
26                     maxLen = len;
27                 }
28             }
29         }
30        
31         return maxLen;
32     }
33 }
View Code

 

　　3.2 Edit distance

 

　　state: f[i][j] 表示a的前i个字符最少药几次编辑可以变成b的前j个字符

　　function： if (a[i - 1] == b [j - 1]) {

　　　　　　　　　dis[i][j] = dis[i - 1][j - 1];　

　　　　　　　} else {

　　　　　　　　　dis[i][j] = Math.min(dis[i - 1][j] + dis[i][j - 1]) + 1;　// 注意 3种情况 不是2种  ❌　

　　　　　　　　　dis[i][j] = Math.min(dis[i - 1][j], Math.min(dis[i][j - 1], dis[i - 1][j - 1])) + 1;　//✅

 

　　　　　　　}

　　initialize: f[i][0] = i; f[0][j] = j;

　　answer: f[m][n]

 

 1 public class Solution {
 2     public int minDistance(String word1, String word2) {
 3         if (word1 == null || word2 == null) {
 4             return 0;
 5         }
 6         int m = word1.length();
 7         int n = word2.length();
 8         if (m == 0 || n == 0) {
 9             return Math.max(m, n);
10         }
11         
12         int[][] dis = new int[m + 1][n + 1];
13         for (int i = 0; i <= m; i++) {
14             dis[i][0] = i;
15         }
16         for (int i = 0; i <= n; i++) {
17             dis[0][i] = i;
18         }
19         
20         for (int i = 1; i <= m; i++) {
21             for (int j = 1; j <= n; j++) {
22                 if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
23                     dis[i][j] = dis[i - 1][j - 1];
24                 } else {
25                     dis[i][j] = Math.min(dis[i - 1][j], Math.min(dis[i][j - 1], dis[i - 1][j - 1])) + 1;
26                 }
27             }
28         }
29         return dis[m][n];
30     }
31 }
Edit distance

 

 

 

　　3.3 Edit distance

 

 

 

　　state: f[i][j] 表示a的前i个字符和b的前j个字符能否交替组成s3的前i ＋ j个字符

　　function:  if (f[i - 1][j] == true && a.charAt(i - 1) == s3.charAt(i + j - 1)  

　　　　　　　　　　|| f[i][j - 1] == true && b.charAt(j - 1)) {

　　　　　　　　　f[i][j] = true;

　　　　　　　} else {

　　　　　　　　　f[i][j] = false;

　　　　　　　}

　　initialize: f[i][0] = i； f[0][i] = i;

　　answer: f[m][n] 

 

Edit distance

 

　　3.4 Distinct Subsequence

　　state: f[i][j]表示s的前i个字符中选取t的前j个字符 有多少种方案

　　function：

　　　　　　　if (a[i - 1] == b [j - 1]) {

 

　　　　　　　　　dp[i][j] = dp[i - 1][j - 1] ＋ dp[i][j - 1];　

 

　　　　　　　} else {

 

　　　　　　　　　dis[i][j] =dp[i - 1][j];

 

　　　　　　　}

　　initialize: f[i][0] = 1; 当目标为空串时，无论source的长度是多少都认为是1个

　　　　　　　f[0][j] = 0; (j > 0)   当两个都为空串的时候，认为是1

　　answer： f[m][n]

 

 1 public class Solution {
 2     public int numDistinct(String s, String t) {
 3         int m = s.length();
 4         int n = t.length();
 5         
 6         int[][] dp = new int[m + 1][n + 1];
 7         for (int i = 0; i <= m; i++) {
 8             dp[i][0] = 1;
 9         }
10         for (int i = 1; i <=n; i++){
11             dp[0][i] = 0;
12         }
13        
14         
15         for (int i = 1; i <= m; i++) {
16             for (int j = 1; j <=n; j++) {
17                 if (s.charAt(i - 1) == t.charAt(j - 1)) { //经常忘了index要减1
18                     dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
19                 } else {
20                     dp[i][j] = dp[i - 1][j];
21                 }
22             }
23         }
24         return dp[m][n];
25     }
26 }
Distinct subsequence

 

　　

　　3.5 Distinct Subsequence

　　state: f[i][j]表示s的前i个字符中选取t的前j个字符 有多少种方案

　　function：

　　　　　　　if (a[i - 1] == b [j - 1]) {

 

　　　　　　　　　dp[i][j] = dp[i - 1][j - 1] ＋ dp[i][j - 1];　

 

　　　　　　　} else {

 

　　　　　　　　　dis[i][j] =dp[i - 1][j];

 

　　　　　　　}

　　initialize: f[i][0] = 1; 当目标为空串时，无论source的长度是多少都认为是1个

　　　　　　　f[0][j] = 0; (j > 0)   当两个都为空串的时候，认为是1

　　answer： f[m][n]

 1 public class Solution {
 2     public boolean isInterleave(String s1, String s2, String s3) {
 3         
 4         if (s1.length() + s2.length() != s3.length()) {
 5             return false;
 6         }
 7         
 8         int m = s1.length();
 9         int n = s2.length();
10        
11         
12         boolean[][] dp = new boolean[m + 1][n + 1];
13         
14         dp[0][0] = true;
15         for (int i = 1; i <= m; i++) {
16             if(s3.charAt(i - 1) == s1.charAt(i - 1) && dp[i - 1][0]) {
17                 dp[i][0] = true;            
18             }
19         }
20         for (int j = 1; j <= n; j++) {
21             if (dp[0][j - 1] == true && s2.charAt(j - 1) == s3.charAt(j - 1)) {
22                 dp[0][j] = true;
23             } 
24         }
25         
26         for (int i = 1; i <= m; i++) {
27             for (int j = 1; j <= n; j++) {
28                // if (dp[i - 1][j - 1] == true && s3.charAt(i + j - 1) == s1.charAt(i - 1) || s3.charAt(i + j -1) == s2.charAt(j - 1)) { 错误的写法1
29               // if ((dp[i - 1][j - 1]  && s3.charAt(i + j - 1) == s1.charAt(i - 1))
30             //    || (dp[i - 1][j - 1] && s3.charAt(i + j - 1) == s2.charAt(j - 1))) {//错误的写法2
31                 if((dp[i - 1][j]  && s3.charAt(i + j - 1) == s1.charAt(i - 1))
32                    || (dp[i][j - 1] && s3.charAt(i + j - 1) == s2.charAt(j - 1))) {
33                     dp[i][j] = true;
34                 }
35                 
36             }
37         }
38         return dp[m][n];
39     }
40 }
Interleaving String

　　

 

4. 划分型动态规划

　　在一个大的区间内找一个小的区间 

　　划分类的题目，基本思路都是用一个local数组和一个gobal数组，然后进行遍历。

　　之所以可以用变量来代替数组，是因为做了滚动数组的优化！

　　4.1Maximum Subarray

　　在一个数组里找一个连续的部分， 使得累加和最大

　　state: local[i] 表示包括第i个元素能找到的最大值

　　　　　 gobal[i] 表示全局前i个元素中能找到的最大值

　　function: 

　　　　　　local[i] = max(local[i - 1] + nums[i], nums[i]);

　　　　　　gobal[i] = max(gobal[i - 1], local[i]);

　　initialization: 

　　　　　　　local[0] = gobal[0] = nums[0];

　　answer: gobal[size - 1];

　　代码：

　　这个代码会超时！

 1 public class Solution {
 2     public int maxSubArray(int[] nums) {
 3         int size = nums.length;
 4         int[] local = new int[size];
 5         int[] gobal = new int[size];
 6         local[0] = nums[0];
 7         gobal[0] = nums[0];
 8         for (int i = 1; i < size; i++) {
 9             local[i] = Math.max(nums[i], local[i - 1] + nums[i]);
10             gobal[i] = Math.max(local[i], gobal[i - 1]);
11         }
12         return gobal[size - 1];
13 
14     }
15 }
Maximum subarray

　　优化：从以上代码，能找到一个精髓的思路在于 local的变量，在拿前i个的最大值＋ nums[i]和第i个值比较. 也就是说，当local[i - 1] < 0 的时候，就丢掉前面的部分！从而，local[i - 1]可以转化为一个prefix sum的概念！

　　

 1 public class Solution {
 2     public int maxSubArray(int[] nums) {
 3         if (nums == null || nums.length == 0) {
 4             return 0;
 5         }
 6         int size = nums.length;       
 7         int preSum = nums[0];
 8         int max = preSum;
 9         
10         for (int i = 1; i < size; i++) {
11             preSum = Math.max(preSum + nums[i], nums[i]);
12             max = Math.max(preSum, max);
13         }
14         return max;
15     }
16 }
preSum 写法1

　　更简洁的判断presum是否大于0的写法

 1 public class Solution {
 2     public int maxSubArray(int[] nums) {
 3         if (nums == null || nums.length == 0) {
 4             return 0;
 5         }
 6         int size = nums.length;       
 7         int preSum = nums[0];
 8         int max = preSum;
 9         
10         for (int i = 1; i < size; i++) {
11             if (preSum > 0) {
12                 preSum += nums[i];
13             }
14             else {
15                 preSum = nums[i];
16             }
17             max = Math.max(max, preSum);
18         }
19         return max;
20     }
21 }
preSum 简洁写法！

 

　　另外一种写法，记录从开始到当前的一个最小值，用当前的累加和剪掉最小值就得到了当前最大的subarray sum

　　　　eg:扫描数组到红色1的位置是，minSum 去除掉了蓝色部分即得到了中间的1的部分

　　　　- 1, - 1, 1, 1 , 1 , 1, -1

 1 public class Solution {
 2     /**
 3      * @param nums: A list of integers
 4      * @return: A integer indicate the sum of max subarray
 5      */
 6     public int maxSubArray(int[] A) {
 7         if (A == null || A.length == 0) {
 8             return 0;
 9         }
10 
11         int sum = 0, max = Integer.MIN_VALUE, minSum = 0;
12         for (int i = 0; i < A.length; i++) {
13             sum += A[i];
14             max = Math.max(max, sum - minSum);
15             minSum = Math.min(minSum, sum);
16         }
17         return max;
18     }
19 }
minSum写法！

　　其实presum的写法是用1次greedy，找到当前累加最大值，把小于0的前缀扔掉。

　　minSum写法的话用了2次greedy，找到当前累加的最大值和累加最小值，用最大值剪掉最小值，由于加法的特性，可以直接扔掉不找到最小值也能拿到答案！

　　

public class Solution {
    /** 马甲变形题，千万注意区分local和gobal的区别，local指的是包含nums[i]的这个最值
     * @param nums: A list of integers
     * @return: An integer indicate the value of maximum difference between two
     *          Subarrays
     */
    public int maxDiffSubArrays(int[] nums) {
        // write your code here
        int size = nums.length;
        int[] left_max = new int[size];
        int[] left_min = new int[size];
        int[] right_max = new int[size];
        int[] right_min = new int[size];
        
        int localMax = nums[0];
        int localMin = nums[0];
        
        left_max[0] = left_min[0] = nums[0];
        //search for left_max
        for (int i = 1; i < size; i++) {
            localMax = Math.max(nums[i], localMax + nums[i]);
            left_max[i] = Math.max(left_max[i - 1], localMax);
        }
        //search for left_min
        for (int i = 1; i < size; i++) {
            localMin = Math.min(nums[i], localMin + nums[i]);
            left_min[i] = Math.min(left_min[i - 1], localMin);
        }
        
        right_max[size - 1] = right_min[size - 1] = nums[size - 1];
        //search for right_max 
        localMax = nums[size - 1];
        for (int i = size - 2; i >= 0; i--) {
            localMax = Math.max(nums[i], localMax + nums[i]);
            right_max[i] = Math.max(right_max[i + 1], localMax);
        }
        //search for right min
        localMin = nums[size - 1];
        for (int i = size - 2; i >= 0; i--) {
            localMin = Math.min(nums[i], localMin + nums[i]);
            right_min[i] = Math.min(right_min[i + 1], localMin);
        }
        //search for separete position 
        int diff = 0;
        for (int i = 0; i < size - 1; i++) {
            diff = Math.max(Math.abs(left_max[i] - right_min[i + 1]), diff);
            diff = Math.max(Math.abs(left_min[i] - right_max[i + 1]), diff);
        }
        return diff;
    }
}
Maximum Subarray Difference

 

　　4.2 Maximum Product Subarray   (Maximum Subarray的马甲变形，总体思路还是一样的）

　　这道题跟MaximumSubarray模型上和思路上都比较类似，还是用一维动态规划中的“局部最优和全局最优法”。这里的区别是维护一个局部最优不足以求得后面的全局最优，这是由于乘法的性质不像加法那样，累加结果只要是正的一定是递增，乘法中有可能现在看起来小的一个负数，后面跟另一个负数相乘就会得到最大的乘积。不过事实上也没有麻烦很多，我们只需要在维护一个局部最大的同时，在维护一个局部最小，这样如果下一个元素遇到负数时，就有可能与这个最小相乘得到当前最大的乘积和，这也是利用乘法的性质得到的。代码如下： 

　　 维护了最大最小2个数组！
　　state:
　　　　min[i] 表示前i个数包括第i个数找到的最小乘积
　　　　max[i]表示前i个数包括第i个数找到的最大乘积
　　function: 
　　　　min[i] = Min(nums[i], Min(min[i - 1]) * nums[i], max[i - 1] * nums[i]) 
　　　　　　　　　　　　　　　　　　　　区分nums[i]正负！！
　　　　max[i] = max(max[i], Max(min[i - 1]) * nums[i], max[i - 1] * nums[i])
 1 public class Solution {
 2     public int maxProduct(int[] nums) {
 3         if (nums == null || nums.length == 0) {
 4             return 0;
 5         }
 6         
 7         int size = nums.length;
 8         int[] min = new int[size];
 9         int[] max = new int[size];
10         min[0] = nums[0];
11         max[0] = nums[0];
12         int result = max[0];
13 
14         for (int i = 1; i < size; i++) {
15             if (nums[i] > 0) {
16                 max[i] = Math.max(nums[i], max[i - 1] * nums[i]);
17                 min[i] = Math.min(nums[i], min[i - 1] * nums[i]);
18             } else {
19                 max[i] = Math.max(nums[i], min[i - 1] * nums[i]);
20                 min[i] = Math.min(nums[i], max[i - 1] * nums[i]);
21             }
22             result = Math.max(result, max[i]);
23             
24         }
25         return result;
26     }
27 }
Maximum product subarray

　　利用滚动数组，把max和min数组优化为o(1)的变量

 1 public class Solution {  
 2     public int maxProduct(int[] A) {  
 3         if(A==null || A.length<1) return 0;  
 4         if(A.length < 2) return A[0];  
 5   
 6         int global = A[0];  
 7         int max = A[0], min = A[0];  
 8         for(int i=1; i<A.length; i++) {  
 9             int a = max*A[i];  
10             int b = min*A[i];  
11               
12             max = Math.max(A[i], Math.max(a, b));  
13             min = Math.min(A[i], Math.min(a, b));  
14             global = Math.max(max, global);  
15         }  
16           
17         return global;  
18     }  
19 }
View Code

　　相关问题： 股票问题

　　　　股票1　　　　

 1 public class Solution {
 2     public int maxProfit(int[] prices) {
 3         if (prices == null || prices.length == 0) {
 4             return 0;
 5         }
 6         int m = prices.length;
 7         int max = 0;
 8         int min = prices[0];
 9         for (int i = 1; i < m; i++) {
10             min = Math.min(min, prices[i]);
11             max = Math.max(max, prices[i] - min);
12         }
13         return max;
14     }
15 }
Best Time to Buy and Sell Stock

　　　　股票2

 1 public class Solution {
 2     public int maxProfit(int[] prices) {
 3         int profit = 0;
 4         for (int i = 0; i < prices.length - 1; i++) {
 5             int diff = prices[i+1] - prices[i];
 6             if (diff > 0) {
 7                 profit += diff;
 8             }
 9         }
10         return profit;
11     }
12 }
best-time-to-buy-and-sell-stock-ii

　　　　股票3

对于2次的题目 一定要想到从左到右和从右到左2次！！！

 1 public class Solution {
 2     public int maxProfit(int[] prices) {
 3         if (prices == null || prices.length <= 1) {
 4             return 0;
 5         }
 6 
 7         int[] left = new int[prices.length];
 8         int[] right = new int[prices.length];
 9 
10         // DP from left to right;
11         left[0] = 0;
12         int min = prices[0];
13         for (int i = 1; i < prices.length; i++) {
14             min = Math.min(prices[i], min);
15             left[i] = Math.max(left[i - 1], prices[i] - min);
16         }
17 
18         //DP from right to left;
19         right[prices.length - 1] = 0;
20         int max = prices[prices.length - 1];
21         for (int i = prices.length - 2; i >= 0; i--) {
22             max = Math.max(prices[i], max);
23             right[i] = Math.max(right[i + 1], max - prices[i]);
24         }
25 
26         int profit = 0;
27         for (int i = 0; i < prices.length; i++){
28             profit = Math.max(left[i] + right[i], profit);  
29         }
30 
31         return profit;
32     }
33 }
View Code

　　　　股票4

　　　　　　当第i天的价格高于第i-1天（即diff > 0）时，那么可以把这次交易（第i-1天买入第i天卖出）跟第i-1天的交易（卖出）合并为一次交易，即local[i][j]=local[i-1][j]+diff；

　　　　　　当第i天的价格不高于第i-1天（即diff<=0）时，那么local[i][j]=global[i-1][j-1]+diff，而由于diff<=0，所以可写成local[i][j]=global[i-1][j-1]。

 

　　　　　　　global[i][j]就是我们所求的前i天最多进行k次交易的最大收益，可分为两种情况：如果第i天没有交易（卖出），那么global[i][j]=global[i-1][j]；如果第i天有交易（卖出），那么global[i][j]=local[i][j]。

 1 public class Solution {
 2     public int maxProfit(int k, int[] prices) {
 3         if (k == 0) {
 4             return 0;
 5         }
 6         int m = prices.length;
 7         if (k >= m / 2) {
 8             int profit = 0;
 9             for (int i = 1; i < m; i++) {
10                 if (prices[i] > prices[i - 1]) {
11                     profit += (prices[i] - prices[i - 1]);
12                 }
13             }
14             return profit;
15         }
16         
17         int[][] mustsell = new int[m + 1][m + 1];// mustSell[i][j] 表示前i天，至多进行j次交易，第i天必须sell的最大获益
18         int[][] gobalmax = new int[m + 1][m + 1];// globalbest[i][j] 表示前i天，至多进行j次交易，第i天可以不sell的最大获益
19         
20         mustsell[0][0] = gobalmax[0][0] = 0;
21         //day zero profit equals 0
22         for (int i = 1; i <= k; i++) {
23             mustsell[0][i] = gobalmax[0][i] = 0;
24         }
25         
26         for (int i = 1; i < m; i++) {
27             int gainorlose = prices[i] - prices[i - 1];
28             mustsell[i][0] = 0;
29             for (int j = 1; j <= k; j++) {
30                 //第一部分为第i天价格高于第i - 1 天，那么可以把第i－1天的交易合并到当天来
31                 //第二部分为第i天的价格低于第i - 1 天， 那么就是用gobal的i - 1天的 j - 1次交易来减掉这次亏损的
32                 mustsell[i][j] = Math.max(mustsell[i - 1][j] + gainorlose, gobalmax[i - 1][j - 1] + gainorlose);
33                 gobalmax[i][j] = Math.max(gobalmax[(i - 1)][j], mustsell[i][j]);
34 
35             }
36         }
37         return gobalmax[(m - 1)][k];
38 
39     }
40 }
股票4

　　　　对于k次交易，k次切分的题目，要想到用动态规划去递增这个交易的次数，成为动归的一个维度。

　　　　对于k = 2 的特殊情况，要想到从左边，右边分别做2次动归就行了！

　　　　　　

　

　　

　　4.3 Maximum Subarray II

　　需要找2段subarray的和

　　思路: 对于两次划分的问题，1. 从左到右 2. 从右到左 做2次单次划分的问题，最后用一次for loop 遍历，寻找2次的切分点

　　对于最后寻找切分点，需要使用gobal的数组！！！千万注意

 1 public class Solution {
 2     /**
 3      * @param nums: A list of integers
 4      * @return: An integer denotes the sum of max two non-overlapping subarrays
 5      */
 6     public int maxTwoSubArrays(ArrayList<Integer> nums) {
 7         // write your code
 8         if (nums == null || nums.size() == 0) {
 9             return 0;
10         }
11         int size = nums.size();
12         int max = Integer.MIN_VALUE;
13         
14         //left to right
15         int leftLocal[] = new int[size];
16         int leftGobal[] = new int[size];
17         leftGobal[0] = leftLocal[0] = nums.get(0);
18         for (int i = 1; i < size; i++) {
19             leftLocal[i] = Math.max(leftLocal[i - 1] + nums.get(i), nums.get(i));
20             leftGobal[i] = Math.max(leftLocal[i], leftGobal[i - 1]);
21         }
22         
23         //right to left
24         int rightLocal[] = new int[size];
25         int rightGobal[] = new int[size];
26         rightLocal[size - 1] = nums.get(size - 1);
27         rightGobal[size - 1] = nums.get(size - 1);
28 
29         for (int i = size - 2; i > 0; i--) {
30             rightLocal[i] = Math.max(rightLocal[i + 1] + nums.get(i), nums.get(i));
31             rightGobal[i] = Math.max(rightLocal[i], rightGobal[i + 1]);
32         }
33 
34         //get total
35         for (int i =  1; i < size; i++) {
36            
37             max = Math.max(leftGobal[i - 1] + rightGobal[i], max);
38         }
39         
40         return max;
41     }
42 }
local,gobal未优化版

　　对于local数组，可以使用滚动数组进行优化为变量，只保留gobal数组。

　　对于local数组进行滚动数组优化的代码如下：

 1 public class Solution {
 2     /**
 3      * @param nums: A list of integers
 4      * @return: An integer denotes the sum of max two non-overlapping subarrays
 5      */
 6     public int maxTwoSubArrays(ArrayList<Integer> nums) {
 7         // write your code
 8         int size = nums.size();
 9         int[] left = new int[size];
10         int[] right = new int[size];
11         int sum = 0;
12         int minSum = 0;
13         int max = Integer.MIN_VALUE;
14         for(int i = 0; i < size; i++){
15             sum += nums.get(i);
16             max = Math.max(max, sum - minSum);
17             minSum = Math.min(sum, minSum);
18             left[i] = max;
19         }
20         sum = 0;
21         minSum = 0;
22         max = Integer.MIN_VALUE;
23         for(int i = size - 1; i >= 0; i--){
24             sum += nums.get(i);
25             max = Math.max(max, sum - minSum);
26             minSum = Math.min(sum, minSum);
27             right[i] = max;
28         }
29         max = Integer.MIN_VALUE;
30         for(int i = 0; i < size - 1; i++){
31             max = Math.max(max, left[i] + right[i + 1]);
32         }
33         return max;
34     }
35 }
2次切分，滚动数组优化local数组

　　4.4 Maximum Subarray III

　　对于N次切分，除了使用local和gobal数组，还需要多开1个维度的变量记录切分次数！

　　State:

　　　　local[i][j]: 表示前i 个数包含第i个元素进行j次操作的最大值

　　　　global[i][j]: 表示前i个数进行j次操作的最大值

　　function:

　　　　local[i][j] = max(local[i - 1][j] + nums[i],

　　　　　　　　　　global[i - 1][j - 1] + nums[i]);

　　　　gobal[i][j] = max(global[i - 1][j],

　　　　　　　　　　　local[i][j])

　　initialization:

　　　　local[i][0] = global[i][0] = 0;

　　Answer:

　　　　global[len][k]

 

 1 public class Solution {
 2     /**
 3      * @param nums: A list of integers
 4      * @param k: An integer denote to find k non-overlapping subarrays
 5      * @return: An integer denote the sum of max k non-overlapping subarrays
 6      */
 7     public int maxSubArray(int[] nums, int k) {
 8         // write your code here
 9         if (nums.length < k) {
10             return 0;
11         }
12         int length = nums.length;
13         
14         int[][] localMax = new int[k + 1][length + 1];
15         int[][] globalMax = new int[k + 1][length + 1];
16         
17         for (int i = 0; i <= k; i++) {
18             localMax[i][0] = 0;
19             globalMax[i][0] = 0;
20         }
21         
22         for (int i = 1; i <= k; i++) {
23             localMax[i][i-1] = Integer.MIN_VALUE;
24             //小于 i 的数组不能够partition
25             for (int j = i; j <= length; j++) {
26                 localMax[i][j] = Math.max(localMax[i][j - 1], globalMax[i - 1][j - 1]) + nums[j-1];
27 
28             /*  1. localMax[i][j - 1] + nums[j - 1]
29                 相当于把最后一次划分向后移一格
30                 2. globalMax[i - 1][j-1]) + nums[j-1]
31                 相当于最后加的一个数作为一个独立的划分！
32             */
33                
34                 if (j == i)//千万注意 i ＝＝ j的时候 只能一种划分！
35                     globalMax[i][j] = localMax[i][j];
36                 else
37                     globalMax[i][j] = Math.max(globalMax[i][j-1], localMax[i][j]);
38 
39             }
40         }
41         return globalMax[k][length];
42     }
43 }
真难！。。。

 

　　

 

 

 

 

 

 

 

 

 

best time to buy and sell stock

5. 背包型动态规划

　　特点： 

　　　　1. 用值作为dp维度

　　　　2. dp过程就是填写矩阵

　　　　3. 可以用滚动数组进行优化

　　5.1 BackPack

　　Given n items with size Ai, an integer m denotes the size of a backpack. How full you can fill this backpack?

　　state: f[i][j] 前i个物体，取出一些能否组成和为S
　　function: 
　　　　　　f[i][j] = 1.  f[i - 1][j - a[i]]   // 能放下第i个物品，那么要看除掉第i 个物品剩下的容量 j - a[i]时候与i － 1个物品的情况

　　　　　　　　　　 2. f[i - 1][j]　　　　//放不下当前第i 个物品，那么它的结果和i - 1个物品是一致的

　　　　　　注意分析这两种情况，并不是并列的，大多数情况下都是和i － 1 个物品是一致的，只有当“破例”的时候，也就是说能装下第i个物品，同时i － 1个物品在j - a[i]容量时也为true.  注意在这部分代码上的处理，很巧妙！

1 f[0][0] = true;
2         for (int i = 0; i < A.length; i++) {
3             for (int j = 0; j <= m; j++) {
4                 f[i + 1][j] = f[i][j];
5                 if (j >= A[i] && f[i][j - A[i]]) {
6                     f[i + 1][j] = true;
7                 }
8             } // for j
9         } // for i
2种情况的处理！

　　answer： 检查f[n][j] 碰到的第一个为真的即为最大值

　　注意：代码上 i的下标的处理，需要注意，通常为dp[i][j] = dp[i - 1][..] 但是按答案这样处理比较简洁。完整代码如下

 1 public class Solution {
 2     /**
 3      * @param m: An integer m denotes the size of a backpack
 4      * @param A: Given n items with size A[i]
 5      * @return: The maximum size
 6      */
 7     public int backPack(int m, int[] A) {
 8         int n = A.length;
 9         boolean dp[][] = new boolean[n + 1][m + 1];
10         
11         dp[0][0] = true;
12         for (int i = 0; i < n; i++) {
13             for (int j = 0; j <= m; j++) {
14                 dp[i + 1][j] = dp[i][j];
15                 if (j >= A[i] && dp[i][j - A[i]]) {
16                     dp[i + 1][j] = true;
17                 }
18             }
19         }
20         
21          for (int i = m; i >= 0; i--) {
22             if (dp[n][i]) {
23                 return i;
24             }
25         }
26         return 0; 
27     }
28 }
backpack

 

　　5.2 backpack ii　　

　　f[i][j]表示前i个物品当中选去一些物品组成容量为j的最大价值

　　下面是没有做滚动数组优化的代码：

 1 public class Solution {
 2     /**
 3      * @param m: An integer m denotes the size of a backpack
 4      * @param A & V: Given n items with size A[i] and value V[i]
 5      * @return: The maximum value
 6      */
 7     public int backPackII(int m, int[] A, int V[]) {
 8         // write your code here
 9         int n  = A.length;
10         int[][] dp = new int[n + 1][m + 1];
11         
12         dp[0][0] = 0;
13         for (int i = 0; i < n; i++) {
14             for (int j = 1; j <= m; j++) {
15                 dp[i + 1][j] = dp[i][j];
16                 if (j >= A[i]) {
17                     dp[i + 1][j] = Math.max(dp[i][j], dp[i][j - A[i]] + V[i]);
18                 }
19             }
20         }
21         return dp[n][m];
22     }
23 }
View Code

　　5.3 k sum

　　从n个数中 取k个数，组成和为target　　

　　　　state: f[i][j][t]前i 个数中去j个数出来能否组成和为t

　　　　function: f[i][j][t] = f[i - 1][j][t] + f[i - 1][j - 1][t - a[i - 1]]

　　　　　　　　　　　　　　不包括第i 个数，组成t的情况＋ 包括第i个数组成t的情况

　　　　犯过的错误：1. 循环的循序问题！

　　　　　　　　　　2.初始化千万注意，对于target ＝ 0， k ＝ 0的时候 是有1种取法，即啥都不取！！！

 1 public class Solution {
 2     /**
 3      * @param A: an integer array.
 4      * @param k: a positive integer (k <= length(A))
 5      * @param target: a integer
 6      * @return an integer
 7      */
 8     public int kSum(int A[], int k, int target) {
 9         int m = A.length;
10         int dp[][][] = new int[m + 1][k + 1][target + 1];
11         // i indicates the item index, j indicate capacity, t means max k
12         dp[0][0][0] = 0;
13         
14         //note!!
15         for (int i = 0; i <= m; i++) {
16             dp[i][0][0] = 1;
17         }
18         
19         for (int i = 0; i < m; i++) {
20             for (int j = 1; j <= k && j <= i + 1; j++) {
21                 for (int t = 1; t <= target; t++) {
22                     dp[i + 1][j][t] = 0;
23                     if (A[i] <= t) {
24                         dp[i + 1][j][t] = dp[i][j - 1][t - A[i]];
25                     }
26                     dp[i + 1][j][t] += dp[i][j][t];
27                 }
28             }
29         }
30         return dp[m][k][target];
31     }
32 }
k sum

 

　　

 

7. 记忆化搜索

　　我们常见的动态规划问题，比如流水线调度问题，矩阵链乘问题等等都是“一步接着一步解决的”，即规模为 i 的问题需要基于规模 i-1 的问题进行最优解选择，通常的递归模式为DP(i)=optimal{DP(i-1)}。而记忆化搜索本质上也是DP思想，当子问题A和子问题B存在子子问题C时，如果子子问题C的最优解已经被求出，那么子问题A或者是B只需要“查表”获得C的解，而不需要再算一遍C。记忆化搜索的DP模式比普通模式要“随意一些”，通常为DP(i)=optimal(DP(j)), j < i。

 

　　7.1.1 Longest Increasing continuous subsequence

　　Give an integer array，find the longest increasing continuous subsequence in this array.

　　An increasing continuous subsequence:

  • Can be from right to left or from left to right.
  • Indices of the integers in the subsequence should be continuous.
　　由于可以从大到小，也可以从小到大，扫2遍数组即可 
 1 public class Solution {
 2     /**
 3      * @param A an array of Integer
 4      * @return  an integer
 5      */
 6     public int longestIncreasingContinuousSubsequence(int[] A) {
 7         // Write your code here
 8         if (A == null || A.length == 0) {
 9             return 0;
10         }
11         int len = 1;
12         int res = 1;
13         for (int i = 1; i < A.length; i++) {
14             if (A[i] > A[i - 1]) {
15                 len++;
16                 res = Math.max(res,len);
17             } else {
18                 len = 1;
19             }
20         }
21         
22         len = 1;
23         for (int i = A.length - 2; i >= 0; i--) {
24             if (A[i + 1] < A[i]) {
25                 len++;
26                 res = Math.max(len, res);
27             } else {
28                 len = 1;
29             }
30         }
31         return res;
32     }
33 }
LICS问题

　　7.1.1 Longest Increasing continuous subsequence 2D

　　Give you an integer matrix (with row size n, column size m)，find the longest increasing continuous subsequence in this matrix. (The definition of the longest increasing continuous subsequence here can start at any row or column and go up/down/right/left any direction). 

　　

　　Given a matrix:

　　[
　　  [1 ,2 ,3 ,4 ,5],
　　  [16,17,24,23,6],
　　  [15,18,25,22,7],
　　  [14,19,20,21,8],
　　  [13,12,11,10,9]
　　]

　　return 25

 

　　对于这道题，用传统的多重循环遇到困难：

  • 从上到下的循环不能解决问题
  • 初始状态找不到　　

　　暴力的方法，从每个点深度优先搜索。

 

　　记忆化搜索vs 普通搜索

　　区别在与用flag数组和dp数组来记录我们曾经遍历过的值，以及这个值的最优解

　　flag数组的作用是保证每个点只遍历一次！！！ 

普通搜索vs记忆化搜索

 

　　flag[i][j]表示 i, j 这个点是否遍历过, 如果遍历过那么直接返回dp[i][j]里面保存的结果就好了！

　　

 

　　state：dp[x][y] 以x,y作为结尾的最长子序列

　　function: 

　　　　遍历x，y上下左右4个格子

　　　　dp[x][y] = dp[nx][ny] + 1  (if a[x][y] > a[nx][ny]);

　　intialize:

　　　　dp[x][y]是极小值时，初始化为1 //表示以xy作为结尾的最长子序列至少是有1个！

　　answer: dp[x][y]中的最大值　　　

 　　这种做法保证了以每个点作为最长子序列的结尾的情况，只会遍历一次。对于已经遍历过的点dp[x][y] 一定是最优解！
　　这道题的另外一个马甲是滑雪题，在二维数组上，只能从大的数往小的数滑，问最长滑多远。
　　我的版本： 
 1 public class Solution {
 2     /**
 3      * @param A an integer matrix
 4      * @return  an integer
 5      */
 6     public int longestIncreasingContinuousSubsequenceII(int[][] A) {
 7         // Write your code here
 8         if(A.length == 0) {
 9             return 0;
10         }
11         int m = A.length;
12         int n = A[0].length;
13         boolean[][] flag = new boolean[m][n];
14         int[][] dp = new int[m][n];
15         int res = 0;
16        
17         for (int i = 0; i < m; i++) {
18             for (int j = 0; j < n; j++) {
19                 dp[i][j] = 1;//长度至少为1，做初始化
20             }
21         }
22         
23         for (int i = 0; i < m; i++) {
24             for (int j = 0; j < n; j++) {
25                 dp[i][j] = search(i, j, dp, flag, A);
26                 res = Math.max(res,dp[i][j]);
27             }
28         } 
29         return res;
30     }
31     
32     int[] array1 = {0, 1, 0, -1, 0};
33     private int search(int x, int y, int[][] dp, boolean[][] flag, int[][] A) {
34         if (flag[x][y] == true) {
35             return dp[x][y];
36         }
37 
38         for (int k = 0; k < 4; k++) {
39             int newx = x + array1[k];
40             int newy = y + array1[k + 1];
41             if (newx < A.length && newx >= 0 && newy >= 0 && newy < A[0].length) {
42                 if (A[x][y] > A[newx][newy]) {
43                     dp[x][y] = Math.max(search(newx, newy, dp, flag, A) + 1, dp[x][y]);
44                 }
45             } 
46             
47         }
48         flag[x][y] = true;
49         return dp[x][y];
50     }
51 }
52
我的版本

注意，九章版本的初始化是在search的同时做的，第40行，ans ＝ 1然后max（ans，search）  很巧妙！

 1 public class Solution {
 2     /**
 3      * @param A an integer matrix
 4      * @return  an integer
 5      */
 6     int [][]dp;
 7     int [][]flag ;
 8     int n ,m;
 9     public int longestIncreasingContinuousSubsequenceII(int[][] A) {
10         if(A.length == 0)
11             return 0;
12         m = A.length;
13         n  = A[0].length;
14         int ans= 0;
15         dp = new int[m][n];
16         flag = new int[m][n];
17         
18         for(int i = 0; i < m; i++) {
19             for(int j = 0; j < n; j++) { 
20                 dp[i][j] = search(i, j, A);
21                 ans = Math.max(ans, dp[i][j]);
22             }
23         }
24         return ans;
25     }
26     int []dx = {1,-1,0,0};
27     int []dy = {0,0,1,-1};
28     
29     int search(int x, int y, int[][] A)   {
30         if(flag[x][y] != 0)    
31             return dp[x][y];
32         
33         int ans = 1; 
34         int nx , ny;
35         for(int i = 0; i < 4; i++) {
36             nx = x + dx[i];
37             ny = y + dy[i];
38             if(0<= nx && nx < m && 0<= ny && ny < n ) {
39                 if( A[x][y] > A[nx][ny]) {
40                     ans = Math.max(ans,  search( nx, ny, A) + 1);
41                 }
42             }
43         }
44         flag[x][y] = 1;
45         dp[x][y] = ans;
46         return ans;
47     }
48 }
View Code

 　　7.2 记忆化搜索与博弈类动态规划结合

　　　　对于博弈类的问题dp[i]只定义一个人的状态，不要同时定义2个人的状态！千万注意！！！

　　　　dp数组，只记录一个人的状态，但是更新的时候要考虑2个人的状态做更新，也就是说第二个人的决策是使得第一个人的结果尽量小！！！

　　　　7.2.1 Coins in a Line

　　　　state: dp[i] 表示现在还剩下i个硬币，前者最后输赢状况

　　　　function： dp[n] = (!dp[n - 1]) || (!dp[n - 2])

　　　　//对于这道题而言，只要前面2个状态不全为true,那么当前的状态就true 其实可以从前往后进行动态规划

　　　　//从前往后动态规划太简单，下面还是用记忆化搜索的方式，从大问题，递归到小问题！

　　　　intialize: dp[0] = false;

　　　　　　　　　dp[1] = true;

　　　　　　　　　dp[2] = true;

　　　　answer: dp[n]

　　　　用递归的方式把大问题转化为小问题

　　　　画搜索树，理解大问题如何转化为小问题！

 

 1 public class Solution {
 2     /**
 3      * @param n: an integer
 4      * @return: a boolean which equals to true if the first player will win
 5      */
 6     public boolean firstWillWin(int n) {
 7         // write your code here
 8         if (n < 3) {
 9             return n > 0;
10         }
11         boolean[] dp = new boolean[n + 1];
12         boolean[] flag = new boolean[n + 1];
13         dp[n] = search(n, dp, flag);
14         return dp[n];
15     }
16     
17     private boolean search(int i, boolean[] dp, boolean[] flag) {
18         
19         if(flag[i] == true) {
20             return dp[i];
21         }
22         
23         if (i < 3) {
24             return dp[i] =  (i > 0);
25         }
26         flag[i] = true;
27         //i - 1, i - 2 不全为true时，dp为true
28         dp[i] = (!search(i - 1, dp, flag)) || (!search (i - 2, dp, flag));
29         return dp[i];
30     }
31 }
记忆化搜索,n很大时会栈溢出

 

　　7.2.2 Coins in a Line II

　　state

　　DP[i]表示从i到end能取到的最大value

　　function

　　当我们走到i时，有两种选择

  1. 取values[i]
  2. 取values[i] + values[i+1]

　　1. 我们取了values[i],对手的选择有 values[i+1]或者values[i+1] + values[i+2] 剩下的最大总value分别为DP[i+2]或DP[i+3],

　　对手也是理性的所以要让我们得到最小value,

　　所以 value1 = values[i] + min(DP[i+2], DP[i+3])

　　2. 我们取了values[i]和values[i+1] 同理 value2 = values[i] + values[i+1] + min(DP[i+3], DP[i+4])

　　最后

　　DP[I] = max(value1, value2)

 　　非递归方式

 1 public class Solution {
 2     /**
 3      * @param values: an array of integers
 4      * @return: a boolean which equals to true if the first player will win
 5      */
 6     public boolean firstWillWin(int[] values) {
 7         // dp 表示从i到end 的最大值
 8         int len = values.length;
 9         // 长度小于2的时候第一个人一定获胜
10         if(len <= 2)
11             return true;
12         int dp[] = new int[len+1];
13         
14         /*初始化，当到达最后3个数字时候，当作特例来处理
15           剩下0个元素，最大能拿到是0
16           剩下1个元素，最大能拿到是当前的那个元素
17           剩下2个元素，最大能拿到是2个都拿走
18           剩下3个元素，第三个肯定拿不到，那么拿到前2个
19         */
20         dp[len] = 0;
21         dp[len-1] = values[len-1];
22         dp[len-2] = values[len-1] + values[len - 2];
23         dp[len - 3] = values[len-3] + values[len - 2];
24         
25         // 动态规划从大到小（从末尾开始，其实还是从小到大，所谓的小是剩下的硬币个数的小到大）
26         for(int i = len - 4;i >= 0; i--){
27             //取1个元素
28             dp[i] = values[i] + Math.min(dp[i+2],dp[i+3]);
29             //取2个元素
30             dp[i] = Math.max(dp[i],values[i]+values[i+1]+ Math.min(dp[i+3],dp[i+4]));
31         }
32         int sum = 0;
33         for(int a:values)
34             sum +=a;
35         return dp[0] > sum - dp[0];
36     }
37 }
Coins in a Line II

 

　　上面的方法略难懂，常规的记忆化搜索的方式为：

　　state: 

　　　　dp[i] 现在还剩i个硬币，先手最多取硬币的价值

　　function:

　　　　n是所有的硬币数目

　　　　pick_one = min(dp[i - 2], dp[i - 3]) + coin[n - i];

　　　　//为什么是coin n - i  eg :  12345 n = 5 i = 3 剩下3个数，取一个数(3, index = 2)的话, index = n - i = 2;

　　　　pick_two = min(dp[i - 3], dp[i -4]) + coin[n - i] + coin[n - i + 1];

　　　　dp[i] = max(pick_one, pick_two);

　　initialize:

　　　　dp[0] = 0;

　　　　dp[1] = coin[length - 1];

　　　　dp[2] = coin[length -2] + coin[length - 1];

　　　　dp[3] = coin[length - 3] + coin[length - 2];

　　Answer:

　　　　dp[n]

 1 public class Solution {
 2     /**
 3      * @param values: an array of integers
 4      * @return: a boolean which equals to true if the first player will win
 5      */
 6     public boolean firstWillWin(int[] values) {
 7         int m = values.length;
 8         int[] dp = new int[m + 1];
 9         boolean[] flag = new boolean[m + 1];
10         
11         int sum = 0;
12         for(int now : values) 
13             sum += now;
14         
15         return sum < 2*search(values.length,values, dp, flag);
16     }
17     
18     private int search(int i, int[] values,int[] dp,boolean[] flag) {
19         if (flag[i] == true) {
20             return dp[i];
21         }
22         flag[i] = true;
23         int n = values.length;
24         if (i == 0) {
25             dp[i] = 0;
26         } else if (i == 1) {
27             dp[i] = values[n - 1];
28         } else if (i == 2) {
29             dp[i] = values[n -1] + values[n - 2];
30         } else if (i == 3) {
31             dp[i] = values[n - 2] + values[n - 3];
32         } else {
33             dp[i] = Math.max(
34                 values[n - i] + Math.min(search(i - 2, values, dp, flag), search(i - 3, values, dp, flag)), 
35                 values[n - i] + values[n - i + 1] + Math.min(search(i - 3, values, dp, flag),  search (i - 4, values, dp, flag)));
36         }
37         return dp[i];
38     }
39 }
View Code

 

　　

 

 

 

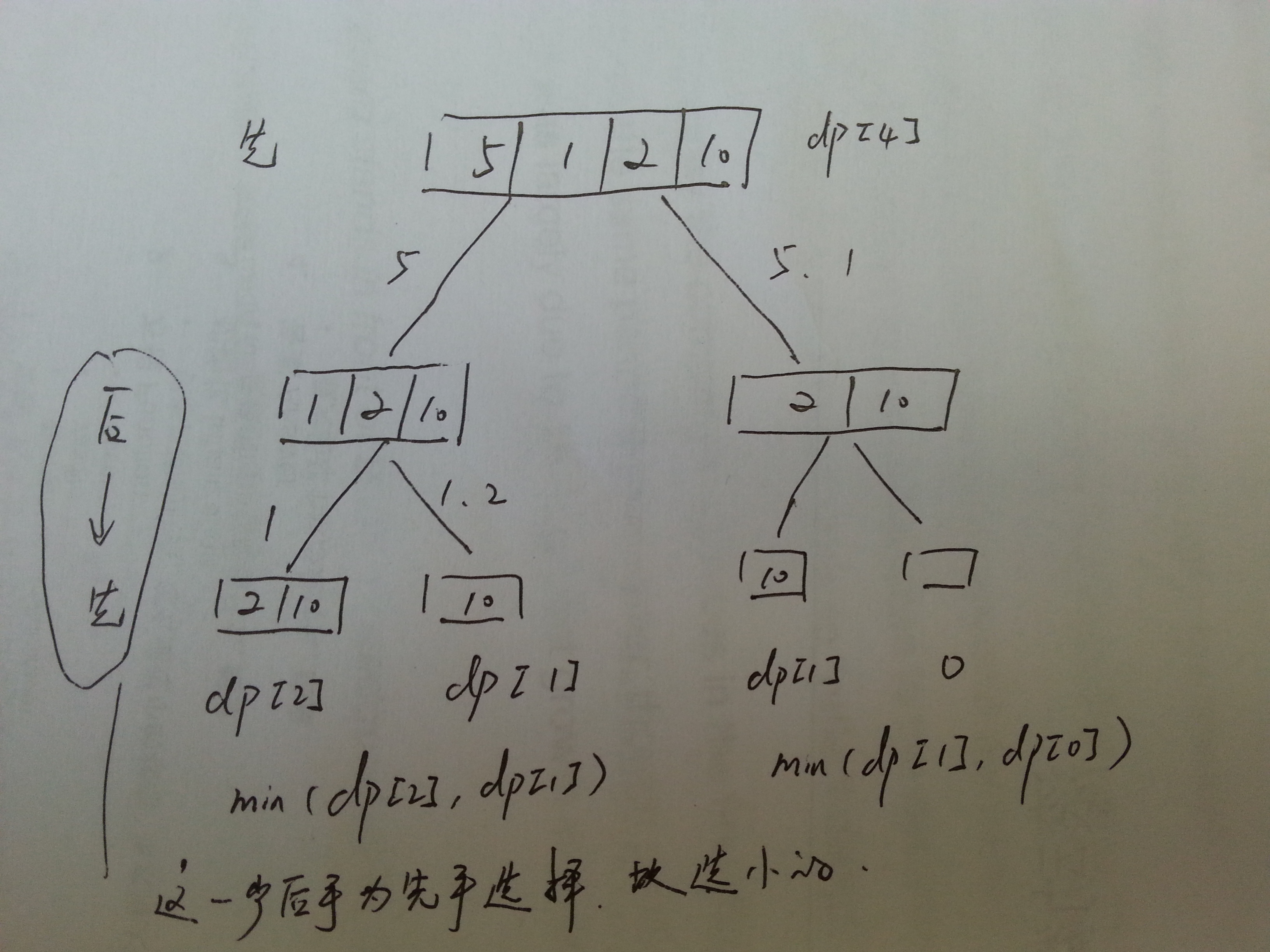
　　7.2.3 Coins in a Line III

　　for 循环的方式：

 1 public class Solution {
 2     /**
 3      * @param values: an array of integers
 4      * @return: a boolean which equals to true if the first player will win
 5      */
 6     public boolean firstWillWin(int[] values) {
 7         // write your code here
 8         if(values.length <= 2) {
 9             return true;
10         }
11         
12         
13         int[][] dp = new int[values.length + 3][values.length + 3];
14         
15         
16         //初始化从第i个位置到第i个位置能拿到的最大值为value［i - 1］
17         for(int i= 1; i <= values.length; i++) {
18             dp[i][i] = values[i - 1];
19         }
20         
21         
22         //dp[i][j] 从第i个位置到第j个位置能取到的最大值
23         int sum = 0;
24         for (int i = values.length; i >= 1; i--) {
25             sum += values[i-1];
26             for (int j = i + 1; j <= values.length; j++) {
27                 //System.out.println("debug i ==" + i+ "debug j ==" + j);
28 
29                 dp[i][j] = Math.max(
30                     values[i - 1] + Math.min(dp[i + 2][j], dp[i + 1][j - 1]),
31                     values[j - 1] + Math.min(dp[i + 1][j - 1], dp[i][j - 2]));
32             }
33         }
34 
35         return dp[1][values.length] > sum - dp[1][values.length];
36     
37     }
38 }
Coins in a Line III

　　记忆化搜索的方式：

　　　　state: dp[i][j] 现在还有第i个到第j个硬币，现在先手取得硬币的最高价值

　　　　function:

　　　　　　pick_left = min(dp[i + 2][j], dp[i + 1][j  - 1]) + coin[i];

　　　　　　pick_right = min(dp[i][j - 2], dp[i + 1][j - 1]) + coin[j];

　　　　　　dp[i][j] = max(pick_left, pick_right);

　　　　intialize:

　　　　　　dp[i][i] = coin[i];

　　　　　　dp[i][i + 1] = max(coin[i], coin[i + 1]);

　　　　answer:

　　　　　　dp[0][n - 1]

　　　　其实代码并不复杂！　　　　　　　　　　　　　

 1 public class Solution {
 2     /**
 3      * @param values: an array of integers
 4      * @return: a boolean which equals to true if the first player will win
 5      */
 6     public boolean firstWillWin(int[] values) {
 7         // write your code here
 8         int n = values.length;
 9         int [][]dp = new int[n + 1][n + 1];
10         boolean [][]flag =new boolean[n + 1][n + 1];
11         
12         int sum = 0;
13         for(int now : values) 
14             sum += now;
15         
16         return sum < 2*MemorySearch(0,values.length - 1, dp, flag, values);
17     }
18     int MemorySearch(int left, int right, int [][]dp, boolean [][]flag, int []values) {
19         
20         if(flag[left][right])   
21             return dp[left][right];
22         flag[left][right] = true;
23         if(left > right) {
24             dp[left][right] = 0;
25         } else if (left == right) {
26             dp[left][right] = values[left];
27         } else if(left + 1 == right) {
28             dp[left][right] = Math.max(values[left], values[right]);
29         } else {
30             int  pick_left = Math.min(MemorySearch(left + 2, right, dp, flag, values), MemorySearch(left + 1, right - 1, dp, flag, values)) + values[left];
31             int  pick_right = Math.min(MemorySearch(left, right - 2, dp, flag, values), MemorySearch(left + 1, right - 1, dp, flag, values)) + values[right];
32             dp[left][right] = Math.max(pick_left, pick_right);    
33         }
34         return dp[left][right];   
35     }
36     
37     
38 }
View Code

　　　7.3 记忆化搜索与区间类动态规划

　　特点：1. 求一段区间的解max/min/count

　　　　　2.转移方程通过区间更新

　　　　　3. 从大到小的更新

　　　7.3.1 stong game

 　　　　死胡同: 容易想到一个思路从小往大，枚举第一次合并在哪？ 就是说拿2颗石头先合并，然后再继续怎么合并，但是这样做，重复的中间变量太多了

　　　　记忆化搜索的思路，从大到小，先考虑最后 0 －（n - 1）次的总花费

　　　　state: dp[i][j]表示把第i到第j所有石子的价值和

　　　　function: 预处理sum[i,j]表示从i到j的所有石子的价值总和

　　　　　　　　dp[i][j] = min(dp[i][k] + dp[k + 1] + sum[i,j]) 对于所有k属于{i,j}

　　　　intialize: 

　　　　　　for each i 

　　　　　　　　dp[i][i] = 0

　　　　answer: dp[0][n - 1]

 1 public class Solution {
 2     /**
 3      * @param A an integer array
 4      * @return an integer
 5      */
 6     public int stoneGame(int[] A) {
 7         if (A == null || A.length == 0) {
 8             return 0;
 9         }
10         
11         int size = A.length;
12         int[][] dp = new int[size][size];
13         int[][] sum = new int[size][size];
14         int[][] flag = new int[size][size];
15         
16         for (int i = 0; i < size; i++) {
17             dp[i][i] = 0;
18             flag[i][i] = 1;
19             sum[i][i] = A[i];
20             for (int j = i + 1; j < size; j++) {
21                 sum[i][j] = sum[i][j - 1] + A[j];
22             }
23         }
24         return search(0, size - 1, dp, sum, flag);
25     }
26     private int search(int left, int right, int[][] dp, int[][] sum, int[][] flag) {
27         if (flag[left][right] == 1) {
28             return dp[left][right];
29         }
30 
31         dp[left][right] = Integer.MAX_VALUE;
32         for (int i= left; i < right; i++) {
33             dp[left][right] = Math.min(dp[left][right], search(left, i, dp, sum, flag) + search(i + 1, right, dp, sum, flag) + sum[left][right]);
34         }
35         flag[left][right] = 1;
36         return dp[left][right];
37     }
38 }
stone game记忆化搜索

　　o(n^2)的外层循环，对每个格子进行记忆化搜索，然后每个格子的区间要遍历切分位又是一层o(n)

　　所以总的是o(n^3)

　　7.3.2 Burst Ballons

　　记忆化搜索的思路： 枚举最后一个打破的气球是哪个！　　

　　　　　　　　　　　　深刻理解，从最后剩下一个气球还是递归，分别求左右两边

　　　　　　　　　　　　对于边界情况的处理，新开了一个数组，两边分别放了一个1！

 1 public class Solution {
 2     public int maxCoins(int[] nums) {
 3         if (nums == null || nums.length == 0) {
 4             return 0;
 5         }
 6         
 7         int m = nums.length;
 8         int[][] flag = new int[m + 2][m + 2];
 9         int[][] best = new int[m + 2][m + 2];
10         int[] array = new int[m + 2];
11         
12         //creat a new array with 1 on two end
13         array[0] = array[m + 1] = 1;
14         for (int i = 1; i <= m; i++) {
15             array[i] = nums[i - 1];
16         }
17         for (int i = 1; i <= m; i++) {
18             for (int j = 1; j <=m; j++) {
19                     best[i][j] = search(flag, best, array, i, j);
20             }
21         }
22         return search(flag, best, array, 1, m);
23     }
24      private int search (int[][] flag, int[][] best, int[] array, int start, int end) {
25          if (flag[start][end] == 1) {
26              return best[start][end];
27          }
28          int res = 0;
29          for (int k = start; k <= end; k++) {
30              int midValue = array[start - 1] * array[k] * array[end + 1];
31              int leftValue = search(flag, best, array, start, k - 1);
32              int rightValue = search(flag,best,array, k + 1, end);
33              res = Math.max(res, leftValue + midValue + rightValue);
34          }
35         best[start][end] = res;
36         flag[start][end] = 1;
37         return res;
38      }
39 }
Burst ballons

 

 

　　其他未分类：

　　8.1 unique binary search tree

　　其实就是枚举每一个点作为根的时候的左右子树的数量

　　首先要明确 count[i]表示有i个数的时候的子树数量

　　比如总数为3的时候 （1， 2， 3）

　　　　1作为根的话，  1的左子树只能有0个点 count[0] 1的右子树有2个点所以count[2]

　　　　2作为根的话， 2的左子树有1这个点， count［1］， 2的右子树只能有3这个点 所以count［1］

　　　　3作为根的话， 3的左子树没有点 count［0］ 3的右子树有2个点 所以 count［2］

　　

 1 public class Solution {
 2 /*
 3 The case for 3 elements example
 4 Count[3] = Count[0]*Count[2]  (1 as root)
 5               + Count[1]*Count[1]  (2 as root)
 6               + Count[2]*Count[0]  (3 as root)
 7 
 8 Therefore, we can get the equation:
 9 Count[i] = ∑ Count[0...k] * [ k+1....i]     0<=k<i-1  
10 
11 */
12     public int numTrees(int n) {
13         int[] count = new int[n+2];
14         count[0] = 1;
15         count[1] = 1;
16     
17         for(int i=2;  i<= n; i++){
18             for(int j=0; j<i; j++){
19                 count[i] += count[j] * count[i - j - 1];
20             }
21         }
22         return count[n];
23     }
24 }
View Code

　　8.2 Unique Binary Search Trees II

　　思路是每次一次选取一个结点为根，然后递归求解左右子树的所有结果，最后根据左右子树的返回的所有子树，依次选取然后接上（每个左边的子树跟所有右边的子树匹配，而每个右边的子树也要跟所有的左边子树匹配，总共有左右子树数量的乘积种情况），构造好之后作为当前树的结果返回。代码如下： 

　　

 1 public class Solution {
 2     public ArrayList<TreeNode> generateTrees(int n) {
 3         return generate(1, n);
 4     }
 5     
 6     private ArrayList<TreeNode> generate(int start, int end){
 7         ArrayList<TreeNode> rst = new ArrayList<TreeNode>();   
 8     
 9         if(start > end){
10             rst.add(null);
11             return rst;
12         }
13      
14             for(int i=start; i<=end; i++){
15                 ArrayList<TreeNode> left = generate(start, i-1);
16                 ArrayList<TreeNode> right = generate(i+1, end);
17                 for(TreeNode l: left){
18                     for(TreeNode r: right){
19 // should new a root here because it need to 
20 // be different for each tree
21                         TreeNode root = new TreeNode(i);  
22                         root.left = l;
23                         root.right = r;
24                         rst.add(root);
25                     }
26                 }
27             }
28         return rst;
29     }
30 }
View Code

　　8.3 perfect square

迷之算法＝ ＝ 

 1 public class Solution {
 2     public int numSquares(int n) {
 3         int[] dp = new int[n + 1];
 4         Arrays.fill(dp, Integer.MAX_VALUE);
 5         for(int i = 0; i * i <= n; i++) {
 6             //1, 4, 9, 16 
 7             dp[i * i] = 1;
 8         }
 9         for (int i = 0; i <= n; ++i)
10             for (int j = 0; i + j * j <= n; ++j)
11                 dp[i + j * j] = Math.min(dp[i] + 1, dp[i + j * j]);
12 
13         return dp[n];
14     }
15 }
View Code

　　

posted @ 2016-10-21 02:16  毛线刷题笔记  阅读(2723)  评论(0)  编辑  收藏  举报