刷题笔记：对撞型／相会型指针（1） two sum类

two sum类题目思路：

　　通过对撞型指针优化算法，根本上其实就是不用扫描多余状态。

if (A[i] + A[j] < sum) {
        j--;
        do someting;
} else if {
        i++;
        do someting;
} else {
  do something;
  i++ or j--;    
}

　　相关题目：

1. two sum　解题报告

Given an array of integers, return indices of the two numbers such that they add up to a specific target.

You may assume that each input would have exactly one solution.

Example:

Given nums = [2, 7, 11, 15], target = 9,

Because nums[0] + nums[1] = 2 + 7 = 9,
return [0, 1].

对于two sum 类问题，可以采用hashmap或者对撞型指针来做。由于返回的是2个目标数的index，这样用两根指针的话，需要额外记录index，相对更繁琐。
方法1： hashmap

public class Solution {
    public int[] twoSum(int[] nums, int target) {
        HashMap<Integer, Integer> map = new HashMap<Integer, Integer>();
        int len = nums.length;
        
        for (int i = 0; i < len; i++) {
            if (map.containsKey(nums[i])) {
                int[] res = new int[] {map.get(nums[i]), i};
                return res;
            }
            map.put(target - nums[i], i);
        }
        return new int[] {0, 0};
    }
}

方法2:两根指针 
需要开辟额外的数组来存原来的数组，因为要返回old index, 也可以新建一个类来保存old index 和 新index的对应关系

public class Solution {
    public int[] twoSum(int[] nums, int target) {
        if (nums == null || nums.length < 2) {
            return new int[]{0,0};
        }
        
        int length = nums.length;
        int sorted[] = new int[length];
        System.arraycopy(nums, 0, sorted, 0, length );
        
        Arrays.sort(nums);
        int i = 0, j = nums.length - 1;
        while (i < j) {
            int sum = nums[i] + nums[j];
            if (sum == target) {
                break;
            } else if (sum > target) {
                j--;
            } else {
                i++;
            }
        }
        int index1 = -1, index2 = -1, current = 0;
        while (index1 == -1 || index2 == -1) {
            if (index1 == -1 && nums[i] == sorted[current]) {
                index1 = current;
                current++;
                continue;
            }
            if (index2 == -1 && nums[j] == sorted[current]) {
                index2 = current;
            }
            current++;
        }
        int[] result = {index1, index2};
        Arrays.sort(result);
        return result;
    }
}

 

2. Two sum II

Given an array of integers, find how many pairs in the array such that their sum is bigger than a specific target number. Please return the number of pairs.

Example

Given numbers = [2, 7, 11, 15], target = 24. Return 1. (11 + 15 is the only pair)

左右两根指针对撞， 当左右之和大于target时候，移动右边的指针，同时ans += （j - i） 因为右边的数加上i-j之间的任何数都会大于target。也就是减少了重复计算，这就是两根指针为什么能够优化n^2到n 

public class Solution {
    public int twoSum2(int[] nums, int target) {
        // Write your code here
        Arrays.sort(nums);
        int i = 0, j = nums.length - 1;
        int ans = 0;
        while (i < j) {
            if (nums[i] + nums[j] <= target) {
                i++;
            } else {
                ans += (j - i);
                j--;
            }
        }
        return ans;
    }
}

 

3. triangleCount

Given an array of integers, how many three numbers can be found in the array, so that we can build an triangle whose three edges length is the three numbers that we find?

Have you met this question in a real interview? 

Yes

Example

Given array S = [3,4,6,7], return 3. They are:

[3,4,6]
[3,6,7]
[4,6,7]

Given array S = [4,4,4,4], return 4. They are:

[4(1),4(2),4(3)]
[4(1),4(2),4(4)]
[4(1),4(3),4(4)]
[4(2),4(3),4(4)]

从右到左遍历第三条边的值，找前两条边能大于第三边的情况，two sum II的马甲变形

public class Solution {
    public int triangleCount(int S[]) {
        // write your code here
        Arrays.sort(S);
        int len = S.length;
        int ans = 0;
        for (int k = len - 1; k > 1; k--) {
            int i = 0, j = k - 1;
            while (i < j) {
                if (S[i] + S[j] > S[k]) {
                    ans += (j - i);
                    j--;
                } else {
                    i++;
                }
            }
        }
        return ans;
    }
}

 

4. sort colors

Given an array with n objects colored red, white or blue, sort them so that objects of the same color are adjacent, with the colors in the order red, white and blue.

Here, we will use the integers 0, 1, and 2 to represent the color red, white, and blue respectively.

因为只有3个颜色需要排序，可以用2根指针遍历一遍数组。更general的做法为counting／bucket sort。

注意它的swap的控制条件和循环结束的控制条件

如果：去除掉等于  while (current < right) 那么会出现下面的错误情况

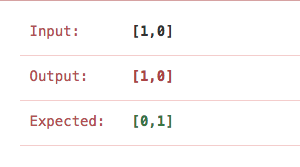
public class Solution {
    public void sortColors(int[] nums) {
        int left = 0, current = 0, right= nums.length - 1;
        while (current <= right) {
            if (nums[current] == 0) {
                swap(left, current, nums);
                left++;
                current++;
            } else if (nums[current] == 2) {
                swap(current, right, nums);
                right--;
            } else {
                current++;
            }
        }
    }
    private static void swap(int i, int j, int[] nums) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

5.  3sum 

Given an array S of n integers, are there elements a, b, c in S such thata + b + c = 0? Find all unique triplets in the array which gives the sum of zero.

 Notice

Elements in a triplet (a,b,c) must be in non-descending order. (ie, a ≤ b ≤ c)

The solution set must not contain duplicate triplets.

Have you met this question in a real interview? 

Yes

Example

For example, given array S = {-1 0 1 2 -1 -4}, A solution set is:

(-1, 0, 1)
(-1, -1, 2)

按照triangle的套路，从末尾开始遍历第三个数，然后中间部分用2根指针。

注意去除重复部分的循环控制条件

我的代码：

public class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> result = new ArrayList<List<Integer>>();
        if (nums == null || nums.length < 3) {
            return result;
        }
        int len = nums.length;
        Arrays.sort(nums);
        for (int k = len - 1; k >= 2; k--) {
            int i = 0, j = k - 1;
            while (i < j) {
                if (nums[i] + nums[j] + nums[k] > 0) {
                    j--;
                } else if (nums[i] + nums[j] + nums[k] < 0) {
                    i++;
                } else {
                    List<Integer> temp = new ArrayList<Integer>();
                    temp.add(nums[i]);
                    temp.add(nums[j]);
                    temp.add(nums[k]);
                    result.add(temp);
                    i++;
                    j--;
                    while(nums[i - 1] == nums[i] && i < k) {
                        i++;
                    }
                    while(nums[j + 1] == nums[j] && j > 0) {
                        j--;
                    }
                }
            }// end of i < j
            while (nums[k] == nums[k - 1] && k >= 2) {
                k--;
            }
        }//end of k
        return result;
    }
}

九章的代码：

判断重复，用了以下代码，果然老司机：

if (i != 0 && num[i] == num[i - 1]) {
　　continue; // to skip duplicate numbers; e.g [0,0,0,0]
}

public class Solution {
    public ArrayList<ArrayList<Integer>> threeSum(int[] num) {
        ArrayList<ArrayList<Integer>> rst = new ArrayList<ArrayList<Integer>>();
        if(num == null || num.length < 3) {
            return rst;
        }
        Arrays.sort(num);
        for (int i = 0; i < num.length - 2; i++) {
            if (i != 0 && num[i] == num[i - 1]) {
                continue; // to skip duplicate numbers; e.g [0,0,0,0]
            }

            int left = i + 1;
            int right = num.length - 1;
            while (left < right) {
                int sum = num[left] + num[right] + num[i];
                if (sum == 0) {
                    ArrayList<Integer> tmp = new ArrayList<Integer>();
                    tmp.add(num[i]);
                    tmp.add(num[left]);
                    tmp.add(num[right]);
                    rst.add(tmp);
                    left++;
                    right--;
                    while (left < right && num[left] == num[left - 1]) { // to skip duplicates
                        left++;
                    }
                    while (left < right && num[right] == num[right + 1]) { // to skip duplicates
                        right--;
                    }
                } else if (sum < 0) {
                    left++;
                } else {
                    right--;
                }
            }
        }
        return rst;
    }
}
 
 © Jiu Zhang 2013-2016. All rights reserved. 京ICP备16004690号-1

6.  3 sum closest

Given an array S of n integers, find three integers in S such that the sum is closest to a given number, target. Return the sum of the three integers. You may assume that each input would have exactly one solution. For example, given array S = {-1 2 1 -4}, and target = 1. The sum that is closest to the target is 2. (-1 + 2 + 1 = 2). 

和triangle count类似的思路，大循环固定1个位置，小循环用2根指针

注意 这道题里面更新最优解不需要放在判断 i++还是j--的里面

代码：

public class Solution {
    /**
     * @param numbers: Give an array numbers of n integer
     * @param target : An integer
     * @return : return the sum of the three integers, the sum closest target.
     */
    public int threeSumClosest(int[] numbers, int target) {
        if (numbers == null || numbers.length < 3) {
            return -1;
        }
        
        Arrays.sort(numbers);
        int bestSum = numbers[0] + numbers[1] + numbers[2];
        for (int i = 0; i < numbers.length; i++) {
            int start = i + 1, end = numbers.length - 1;
            while (start < end) {
                int sum = numbers[i] + numbers[start] + numbers[end];
                if (Math.abs(target - sum) < Math.abs(target - bestSum)) {
                    bestSum = sum;
                }
                if (sum < target) {
                    start++;
                } else {
                    end--;
                }
            }
        }
        
        return bestSum;
    }
}

7. 4 sum

Given an array S of n integers, are there elements a, b, c, and d in S such that a + b + c + d = target? Find all unique quadruplets in the array which gives the sum of target.

Note: The solution set must not contain duplicate quadruplets.

For example, given array S = [1, 0, -1, 0, -2, 2], and target = 0.

A solution set is:
[
  [-1,  0, 0, 1],
  [-2, -1, 1, 2],
  [-2,  0, 0, 2]
]

 

可以在3 sum的基础上加一层for循环。 但不是最优解。注意这种方法去重的控制条件

public class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        if (nums == null || nums.length < 4) {
            return res;
        }
        int len = nums.length;
        Arrays.sort(nums);
        for (int i = 0; i < len - 2; i++) {
            if (i != 0 && nums[i] == nums[i - 1]) {
                continue;
            }
            for (int j = i + 1; j < len - 1; j++) {
                if (j != i + 1 && nums[j] == nums[j - 1]) {
                    continue;
                }
                int left = j + 1, right = len - 1;
                while (left < right) {
                    int sum = nums[i] + nums[j] + nums[left] + nums[right];
                    if (sum == target) {
                        List<Integer> temp = new ArrayList<Integer>();
                        temp.add(nums[i]);
                        temp.add(nums[j]);
                        temp.add(nums[left]);
                        temp.add(nums[right]);
                        res.add(temp);
                        left++;
                        right--;
                        while (left < right && nums[left] == nums[left - 1]) {
                            left++;
                        }
                        while (left < right && nums[right] == nums[right + 1]) {
                            right--;
                        }
                    } else if (sum > target) {
                        right--;
                    } else {
                        left++;
                    }
                } // end of left < right
            }// end of j
        } // end of i
        return res;
    }
}

有n^2的解法//to do 以后再说 

 

8. K sum

其实是个动态规划：

从n个数中 取k个数，组成和为target　　

　　　　state: f[i][j][t]前i 个数中去j个数出来能否组成和为t

　　　　function: f[i][j][t] = f[i - 1][j][t] + f[i - 1][j - 1][t - a[i - 1]]

　　　　不包括第i 个数，组成t的情况＋ 包括第i个数组成t的情况

注意第二层循环的时候，都要考虑== 即 从i个数里面取出j个，那个 i== j 那么就是全都取出来， j == k 意味着取出k个数

代码：

public class Solution {
    public int kSum(int A[], int k, int target) {
        // write your code here
        if (A == null || A.length < k) {
            return 0;
        }
        int len = A.length;
        int[][][] dp = new int[len + 1][k + 1][target + 1];
        
        for (int i = 0; i < len; i++) {
            dp[i][0][0] = 1;
        }
        
        for (int i = 1; i <= len; i++) {
            for (int j = 1; j <= i && j <= k; j++) {
                for (int t = 0; t <= target; t++) {
                    dp[i][j][t] = dp[i - 1][j][t];
                    if (t >= A[i - 1]) {
                        dp[i][j][t] += dp[i - 1][j - 1][t - A[i - 1]];
                    }
                }
            }
        }
        return dp[len][k][target];
    }
}