DBoW2算法原理介绍

本篇介绍DBoW2算法原理介绍，下篇介绍DBoW2的应用。

DBow2算法

DBow2是一种高效的回环检测算法，DBOW2算法的全称为Bags of binary words for fast place recognition in image sequence，使用的特征检测算法为Fast，描述子使用的是brief描述子，（TODO:和DBow的区别在哪里？）是一种离线的方法。

二进制特征（ORB特征）：Fast特征点+Brief描述子
（Hamming distance） 256bits的二进制描述符
Brief描述子：\(b=[b_1, b_2, \cdots, b_{256}]\)总共256bits，每一个bit都是0,1的数
Surf描述子：64位的浮点数,\(d=[d_1, d_2, \cdots, d_{64}]\)

基本的数学知识

Brief使用的距离描述算子为Hamming距离，定义如下：

\[d(v_1, v_2) =\vert v_{11} - v_{21} \vert + \vert v_{12} - v_{22} \vert + \cdots + \vert v_{1n} - v_{2n} \vert \]

对于二进制字符串可以通过简单的按位异或实现\(d(v_1,v_2) = v_1 \oplus v_2\)。

算法流程

Bag of Words字典建立方法（最终得到的就是每一层的不同类的median，每一个叶节点对应的就是一个词汇）：

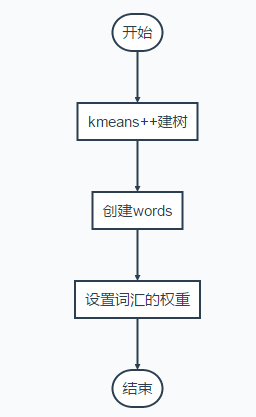
建树流程

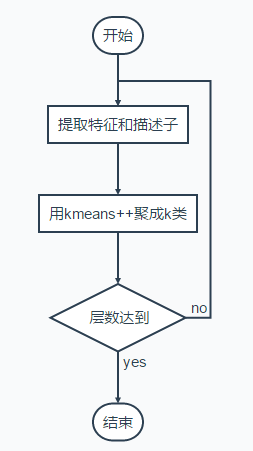
kmeans++方法
输入：（a）聚类数目；（2）初始化中心点（这里使用kmeans++的方法）
算法流程：
迭代：
（1）每个点分类到最近的中心点；
（2）用每一类点的中心点更新中心点。

中心点初始化方法：
-（1）从输入的点集合中随机选择一个点作为第一个聚类中心；
-（2）对于数据集中的每一个点，计算它与已选择的最近的聚类中心的距离D(x)；
-（3）选择一个新的数据点作为新的聚类中心，选择的原则是：D(x)较大的点，被选为聚类中心的概率较大；
-（4）重复2和3的步骤直到k个聚类中心被选出来；
D(x)到概率上的反应：

• 先从数据库随机挑个随机点当“种子点”
• 对于每个点，计算其和最近的一个“种子点”的距离D(x)并保存在一个数组里，然后把这些距离加起来得到Sum(D(x))。
• 然后，再取一个随机值，用权重的方式来取计算下一个“种子点”。这个算法的实现是，先取一个能落在Sum(D(x))中的随机值Random，然后用Random -= D(x)，直到其<=0，此时的点就是下一个“种子点”。

k-median方法在聚类方法的第二步使用每一个类的中值作为新的中心；

创建words：把建树中所有的节点遍历一遍，找出叶节点。

DBoW2创建节点代码：

\\把所有的节点遍历一遍
for(++nit; nit != m_nodes.end(); ++nit)
{
	  \\只有节点是字符
      if(nit->isLeaf())
      {
        nit->word_id = m_words.size();
        m_words.push_back( &(*nit) );
      }
}

权重设置

权重设置用的是idf，意思是词汇在训练过程中出现的频率越高，区分度越低，因此权重越低。

\[idf=\log\frac{N}{n_i} \]

每一个节点包括（只列出了部分信息）

struct Node 
{
	//在所有节点中的标号
	NodeId id;
	//该节点的权重，该权重为
	//训练的过程中设置的，在得到了树之后，将所有的描述子
	//过一遍树，得到每个单词出现的次数，除以总的描述子数目
	WordValue weight;
	//描述符，为每一类的均值（对于brief描述子，则要对均值进行二值化）
	TDescriptor descriptor;
	//如果是叶节点，则有词汇的id
	WordId word_id;
}

[说明]：上面的方法是分层聚类的，每一次聚类得到的多个节点，都有median \(v\)表
示该类，可以用来判断新的词汇是否属于该类。最终建立的树包括W个叶节点，也就是W个视觉词汇，词汇也用median表示。