[UFLDL] *Sparse Representation
稀疏表达(sparse representation)
这个东西好,原因之一是更接近生物的认知过程。
可以先看下lasso [Scikit-learn] 1.1 Generalized Linear Models - Lasso Regression,再看此篇会容易理解些。
简单地说,它能尽可能地仅仅保留重要的特征为激活状态。
《CMU 10-702 Sparsity and the lasso》
(1) 何为稀疏(What’s sparsity)
From: http://www.cnblogs.com/tornadomeet/archive/2013/03/19/2970101.html
一般使得隐含层小于输入结点的个数,但是我们也可以让隐藏层的节点数大于输入结点的个数,只需要对其加入一定的稀疏限制就可以达到同样的效果。
如何让隐藏层的节点中大部分被抑制,小部分被激活,这就是稀疏。
那什么是抑制,什么是激活能?
-
- 如果是sigmoid函数,当神经元的输出接近1时为激活,接近0时为稀疏;
- 如果采用tanh函数,当神经元的输出接近1时为激活,接近-1时为稀疏。
那添加什么限制可以使的隐含层的输出为稀疏呢?稀疏自动编码希望让隐含层的平均激活度为一个比较小的值。
Hidden层的平均激活的数据表示为:
其中, 表示在输入数据为x的情况下,隐藏神经元j的激活度。
为了使得均激活度为一个比较小的值,引入 ,称为稀疏性参数,一般是一个比较小的值,使得
这样就可以是隐含层结点的活跃度很小。
(2) Sparse Autoencoder 带约束的AutoEncoder
稀疏编码是对网络的隐含层的输出有了约束,即隐含层节点输出的平均值应尽量为0,这样的话,大部分的隐含层节点都处于非activite状态。因此,此时的sparse autoencoder损失函数表达式为:
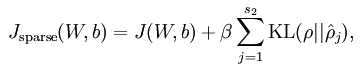
无稀疏约束时网络的损失函数表达式如下:
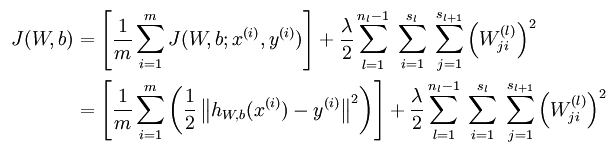
后面那项为KL距离,其表达式如下:
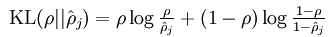
隐含层节点输出平均值求法如下:
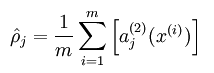
其中的参数一般取很小,比如说0.05,也就是小概率发生事件的概率。这说明要求隐含层的每一个节点的输出均值接近0.05(其实就是接近0,因为网络中activite函数为sigmoid函数),这样就达到稀疏的目的了。
KL距离在这里表示的是两个向量之间的差异值。从约束函数表达式中可以看出,差异越大则”惩罚越大”,因此最终的隐含层节点的输出会接近0.05。
读后感:
其实就是如何加约束能达到”消减feature“的目的。
到这里我们warm up完毕。
Background
通过实例先了解这个东西能做什么:稀疏编码(Sparsecoding)在图像检索中的应用
目的:提高检索的效果
1.1 图像预处理
图像预处理主要作用是去除图片噪声,去除相关性,加强边缘等,以提高后续特征抽取的有效性。常见的图片预处理有白化,高通滤波,低通滤波,高斯去噪等。
1.2 特征提取
特征提取在图像检索中处于核心地位,有效的特征能够表达出一幅图像所描述的某些特定内容。常见的特征有SIFT,SURF,Gabor纹理特征,Gist,颜色直方图,DAISY,ORB,HOG等。
1.3 特征融合
这里的特征融合是针对一种局部特征(描述子)来进行的,当某个描述子在不同图片上抽取出的数目不定时,有必要使得所有的图片具有统一维度的特征向量表达。常见的有效的方式是使用文本挖掘中的词袋(BOW,也称BOF)的思想。
生物意义 and 数学意义
稀疏编码在人脸识别,信号去噪,图像重建,超像素,图像分割,图像分类,背景建模方面都有很好的效果。
稀疏性被解释为人眼视觉层中的V1层 [link],具备了人眼识别物体的基础特性。这种视觉特性使得其特别适合图像相关的处理和识别。
链接:https://www.zhihu.com/question/22205661/answer/152655757

超完备字典的学习
可以根据具体的任务使用不同的算法,目前常用的是:
- KSVD算法重点在保证重建误差最低来构造完备字典;
- DKSVD算法引入了判别模型,使得训练的字典具有可区分性;
- DDL算法引入了训练集之间的关联性和判别模型,使得字典更具有可区分性;
- AutoEncoder算法 + 稀疏条件; <----
稀疏编码与图像检索
稀疏编码的明显的优点是能够重建信号,能去除噪声,抗部分丢失性,更具有表达粒度,学习字典可以是完全无监督学习,或者有监督学习。
-
- 首先是该字典是由类中心组成的,未必能覆盖图片局部特征点的空间,即该字典未必是完备的。
- 其次是字典构建的过程中只考虑了局部特征点之间的相似程度,且局部特征点仅与一个字典基元关联,并未考虑局部特征点与其他字典基元的关联。
先吐槽一下主角
From: sparse autoencoder, sparse coding和restricted boltzmann machine的关系?
我的看法是:这三者基本是一致的,
-
- sparse coding 的坏处在于当我们通过training得到一个Dictionary后,给定任意一个测试样本x,我们还得求解一个|x - Du| + a|u|的优化才能得到u,这简直是个噩梦;
- sparse autoencoder 则是learn了一个映射函数f(x) = u,使得给定x就能迅速得到一个u;
- rbm 就和autoencoder更像了,只不过后者是对权值施加sparse约束,rbm施加了正交矩阵约束(也就是你说的来和去共享权值)
我们需要一些约束
”凸优化“ 是指一种比较特殊的优化,是指目标函数为凸函数且由约束条件得到的定义域为凸集的优化问题,也就是说目标函数和约束条件都是”凸”的。
Sparse coding是将输入的样本集X分解为多个基元的线性组合,然后这些基前面的系数表示的是输入样本的特征。其分解公式表达如下:
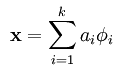
一般情况下要求基的个数k非常大,至少要比x中元素的个数n要大,因为这样的基组合才能更容易的学到输入数据内在的结构和特征。
-
- 在常见的PCA算法中,是可以找到一组基来分解X的,只不过那个基的数目比较小,所以可以得到分解后的系数a是可以唯一确定,
- 在sparse coding中,k太大,比n大很多,其分解系数a不能唯一确定。
* 对ai约束 *
所以,一般的做法是对系数a作一个稀疏性约束,这也就是sparse coding算法的来源。
此时系统对应的代价函数(前面的博文都用损失函数表示,以后统一改用代价函数,感觉这样翻译更贴切)表达式为:
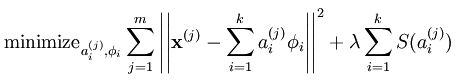
第一项,重构输入数据X的代价值;
第二项,S(.)为分解系数的系数惩罚,lamda是两种代价的权重,是个常量。
* 对基约束 *
但是这样还是有一个问题,比如说我们可以将系数a减到很小,且将每个基的值增加到很大,这样第一项的代价值基本保持不变,而第二项的稀疏惩罚依旧很小,达不到我们想要的目的,即:
分解系数中只有少数系数远远大于0,而不是大部分系数都比0大(虽然不会大太多)。
解决这个问题的通用方法是是对基集合中的值也做了一个约束,约束后的系统代价函数为:
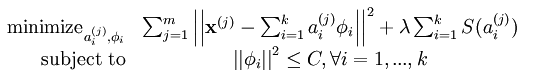
Sparse coding的statistics解释:
主要是从概率的角度来解释sparse coding方法,不过这一部分的内容还真没太看明白,只能讲下自己的大概理解。如果把误差考虑进去后,输入样本X经过sparse coding分解后的表达式则如下:
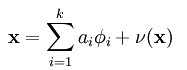
而我们的目标是找到一组基Ф,使得输入样本数据出现的概率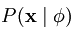 与输入样本数据的经验分布概率
与输入样本数据的经验分布概率 最相近,如果用KL距离来衡量其相似度的话,就是满足他们的KL距离最小,即下面表达式值最小:
最相近,如果用KL距离来衡量其相似度的话,就是满足他们的KL距离最小,即下面表达式值最小:

由于输入数据的经验分布函数概率是固定值,所以求上式值最小相当等价于求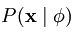 最大。
最大。
经过对参数a的先验估计和函数积分值估计等推导步骤,最后等价于求下面的能量函数值最小:

而这就很好的和sparse coding的代价函数公式给联系起来了。
到目前为止我们应该知道sparse coding的实际使用过程中速度是很慢的,因为即使我们在训练阶段已经把输入数据集的基Ф学习到了,在测试阶段时还是要通过凸优化的方法去求得其特征值(即基组合前面的系数值),所以这比一般的前向神经网络速度要慢(一般的前向算法只需用矩阵做一下乘法,然后做下加法,求个函数值等少数几步即可完成)。
Sparse coding的autoencoder解释:
首先来看看向量X的Lk规范数,其值为:![]() 由此可知,L1范数为各元素之和,L2范数为该向量到远点的欧式距离。
由此可知,L1范数为各元素之和,L2范数为该向量到远点的欧式距离。
用矩阵的形式来表达sparse coding的代价函数如下:
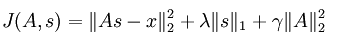
和前面所讲的一样,这里也对基值s做了稀疏性惩罚,用的是L1范数来约束,同时也防止系数矩阵A过大,对其用的是L2范数的平方来约束。但是基值处的L1范数在0点是无法求导的,所以不能用梯度下降等类似的方法来对上面的代价函数求最优参数,于是为了在0处可导,可将公式变成如下:
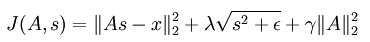
continue...
关于这部分内容,暂停,UFLDL的内容不足以深刻认识,打算读论文研读,另起一系列。
在稀疏编码中”标注值”也是需要的,只不过它的输出理论值是本身输入的特征值x,其实这里的标注值y=x。这样做的好处是,网络的隐含层能够很好的代替输入的特征;



