[UFLDL] Generative Model
这一部分是个坑,应该对绝大多数菜鸡晕头转向的部分,因为有来自物理学界的问候。
- 采样方法
[Bayes] runif: Inversion Sampling
[Bayes] dchisq: Metropolis-Hastings Algorithm
[Bayes] Metroplis Algorithm --> Gibbs Sampling
- 能量传播
纵观大部分介绍RBM的paper,都会提到能量函数。因此有必要先了解下能量函数的概念。参考网页http://202.197.191.225:8080/30/text/chapter06/6_2t24.htm关于能量函数的介绍:
一个事物有相应的稳态,如在一个碗内的小球会停留在碗底,即使受到扰动偏离了碗底,在扰动消失后,它会回到碗底。学过物理的人都知道,稳态是它势能最低的状态。因此稳态对应与某一种能量的最低状态。
将这种概念引用到Hopfield网络中去,Hopfield构造了一种能量函数的定义。这是他所作的一大贡献。引进能量函数概念可以进一步加深对这一类动力系统性质的认识,可以把求稳态变成一个求极值与优化的问题,从而为Hopfield网络找到一个解优化问题的应用。
- 目的:能量值最小
1) 联合概率为:
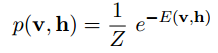
RBM模型的能量函数:
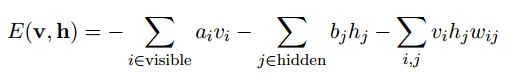
Z是归一化因子,其值为:
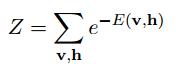
2) 边缘分布为:

【这里为了习惯,把输入v改成函数的自变量x】
令一个中间变量F(x)为:
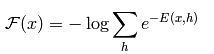
边缘分布为重新写为:

这时候它的偏导函数取负,变为:
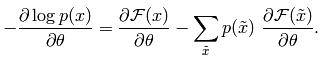
从上面能量函数的抽象介绍中可以看出,如果要使系统(这里即指RBM网络)达到稳定,则应该是:
系统的能量值E最小 --> F(x)最小 --> P(x)最大 --> 损失函数 as -P(x)
上述就是基本原理,但问题在于计算繁复,例如Z的计算O(2m+n),所以需要下面的CD算法。
- 对比散度算法(CD: contractive divergence)前夜!
受限波尔兹曼机RBM的基本模型
如何理解 p(v,h|theta) ? 注意下面的式子的Wi,j,以及ai, bj的意义。
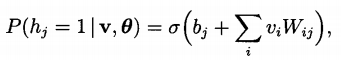
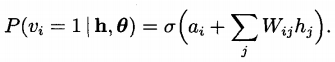
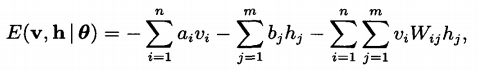
基于对比散度的RBM快速学习算法
似然函数如下:
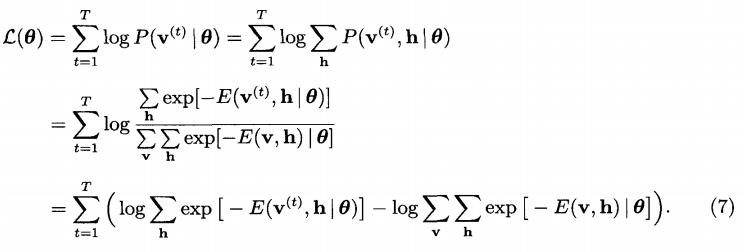
注意最后的结论:
第一项,v是具体的观察样本,故好求;
第二项,Z的计算O(2m+n),故不好求;
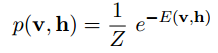
但是可以通过gibbs采样获取近似值,原理参见:[Bayes] Metroplis Algorithm --> Gibbs Sampling

- 关于”重构“,从而能计算误差
From: 限制Boltzmann机(Restricted Boltzmann Machine)
问题在于没有标签,没有误差,无法训练W,所以无法训练出P(v)的概率分布。
所以早期的RBM采用从h重构v'来计算误差。重构v',说的好像挺简单,但是需要知道P(v,h)的联合概率分布,用这概率分布去生成v'。
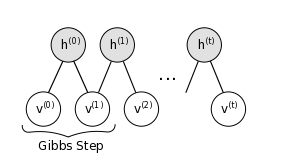
上图是一条波动的链,v0->h0普通的正向传播,忽略不计。
从h0,正式开始Gibbs采样,一个step过程为,hn->vn+1->hn+1,即hvh过程。
当t→∞时,有vt=v'
- 对比散度算法(CD: contractive divergence)今日!
如何利用”重构“来更新theta = {a, b, w}的问题。
算法如下,hvh过程。可见我们有了”计算误差“的方式。

可见,rbm也是一个类似于autoencoder的过程,hidden layer提取出了样本特征。
- 与AutoEncoder的关系
准确来说,AutoEncoder是RBM的简化衍生物。
-
- RBM是一个概率生成模型 --> 使用概率方法训练
- AutoEncoder只是一个普通的模型 --> 使用bp训练
绕了个弯子的选择重构
神经网络的本质是训练岀能够模拟输入的W,这样,在测试的时候,遇到近似的输入,W能够做出漂亮的响应。
RBM选择概率,是因为有概率论的公式支持。这样优化网络,能够达到上述目标。
只是原始目标不好优化,Hinton才提出对比训练的方法,即绕了个弯子的选择重构。
两者近似等价
能量函数使得W朝更大概率方向优化。但是,正如线性回归有最小二乘法和高斯分布(贝叶斯线性回归)两种解释一样。
其实,W的训练大可不必拘泥于概率,AutoEncoder则绕过了这点,直接选择了加权重构,所以cost函数简单。
【相对于rbm,AutoEncoder是两套参数W,且不一样】
可以这么说,重构的数学理论基础就是RBM的原始目标函数。而概率重构启发了直接重构,两者近似等价。
梯度法的一次重构效果出奇好
从马尔可夫链上看,AutoEncoder可看作是链长为1的特殊形式,即一次重构,而RBM是多次重构。
能使用直接重构的另一个原因是,Hinton在实验中发现,梯度法的一次重构效果出奇好。
所以AutoEncoder中摒弃了麻烦的Gibbs采样过程。
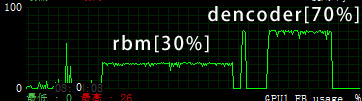
从GPU计算来看,k=1情况下,AutoEncoer的GPU利用率高(70%),RBM利用率低(30%),一开始实现的时候吓了一跳。
CUDA执行马尔可夫链效率并不高,目测二项分布随机重构是由CPU执行的。
尤其在把batch_size设为600之后,RBM的GPU利用率居然只有(10%), 所以官方教程把batch_size设为了20,来减小概率生成的计算压力。
当然k=15时,GPU加速之后仍然十分缓慢。RBM不愧是硬件杀手。
(本图来自MSI Afterburner,GTX 765M,OC(847/2512/913))
抛出一个问题:VAE又是怎么一回事?具有哪些优势?
Goto: [Bayesian] “我是bayesian我怕谁”系列 - Variational Autoencoders
用NN(神经网络)来对数据进行大量的降维是从2006开始的,这起源于2006年science上的一篇文章:reducing the dimensionality of data with neural networks,作者就是鼎鼎有名的Hinton,这篇文章也标志着deep learning进入火热的时代。
-
- 权值太大的话,就很容易收敛到”差”的局部收敛点;
- 权值太小的话则在进行误差反向传递时离输入层越近的权值更新越慢【梯度消失】;
因此优化问题是多层NN没有大规模应用的原因,而autoencoder深度网络确能够较快的找到比较好的全局最优点,
它是用无监督的方法(这里是RBM)
- 先分开对每层网络进行训练,
- 然后将它当做是初始值来微调。
这种方法被认为是对PCA的一个非线性泛化方法。
DBM由多个RBM叠加起来
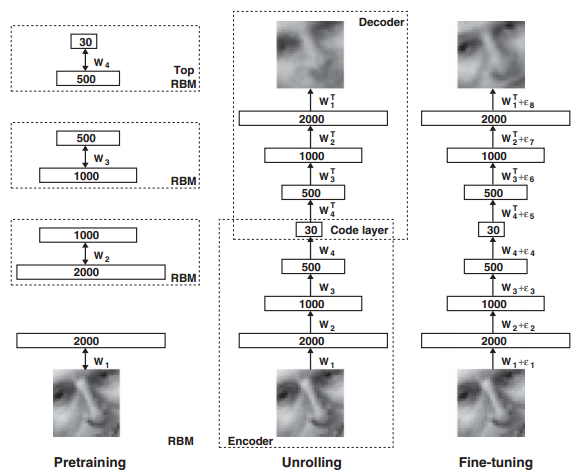
由上图可以看到,当网络的预训练过程完成后,我们需要把解码部分重新拿回来展开构成整个网络,然后用真实的数据作为样本标签来微调网络的参数。
当网络的输入数据是连续值时,只需将可视层的二进制值改为服从方差为1的高斯分布即可,而第一个隐含层的输出仍然为二进制变量。
文章中包含了多个实验部分,有手写数字体的识别,人脸图像的压缩,新闻主题的提取等。在这些实验的分层训练过程中,其第一个RBM网络的输入层都是其对应的真实数据,且将值归一化到了(0,1).而其它RBM的输入层都是上一个RBM网络输出层的概率值;但是在实际的网络结构中,除了最底层的输入层和最顶层RBM的隐含层是连续值外,其它所有层都是一个二值随机变量。此时最顶层RBM的隐含层是一个高斯分布的随机变量,其均值由该RBM的输入值决定,方差为1。
实验结果1:
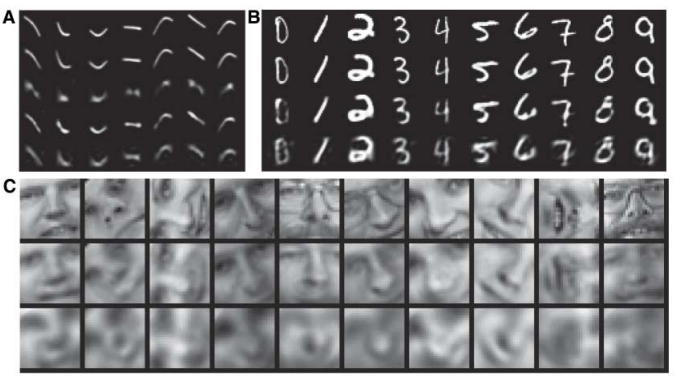
这3副图中每幅图的最上面一层是原图,其后面跟着的是用NN重构的图,以及PCA重构的图(可以选取主成分数量不同的PCA和logicPCA或者标准PCA的组合,本人对这logicPCA没有仔细去研究过)。其中左上角那副图是用NN将一个784维的数据直接降到6维!
作者通过实验还发现:如果网络的深度浅到只有1个隐含层时,这时候可以不用对网络进行预训练也同样可以达到很好的效果,但是对网络用RBM进行预训练可以节省后面用BP训练的时间。另外,当网络中参数的个数是相同时,深层网络比浅层网络在测试数据上的重构误差更小,但仅限于两者参数个数相同时。作者在MINIST手写数字识别库中,用的是4个隐含层的网络结构,维数依次为784-500-500-2000-10,其识别误差率减小至1.2%。预训时练得到的网络权值占最终识别率的主要部分,因为预训练中已经隐含了数据的内部结构,而微调时用的标签数据只对参数起到稍许的作用。
MINST降维实验:
本次是训练4个隐含层的autoencoder深度网络结构,输入层维度为784维,4个隐含层维度分别为1000,500,250,30。整个网络权值的获得流程梳理如下:
- 首先训练第一个rbm网络,即输入层784维和第一个隐含层1000维构成的网络。采用的方法是rbm优化,这个过程用的是训练样本,优化完毕后,计算训练样本在隐含层的输出值。
- 利用1中的结果作为第2个rbm网络训练的输入值,同样用rbm网络来优化第2个rbm网络,并计算出网络的输出值。并且用同样的方法训练第3个rbm网络和第4个rbm网络。
- 将上面4个rbm网络展开连接成新的网络,且分成encoder和decoder部分。并用步骤1和2得到的网络值给这个新网络赋初值。
- 由于新网络中最后的输出和最初的输入节点数是相同的,所以可以将最初的输入值作为网络理论的输出标签值,然后采用BP算法计算网络的代价函数和代价函数的偏导数。
- 利用步骤3的初始值和步骤4的代价值和偏导值,采用共轭梯度下降法优化整个新网络,得到最终的网络权值。以上整个过程都是无监督的。




