[UFLDL] Dimensionality Reduction

博客内容取材于：http://www.cnblogs.com/tornadomeet/archive/2012/06/24/2560261.html

Deep learning：三十五(用NN实现数据降维练习)
Deep learning：三十四(用NN实现数据的降维)
Deep learning：三十三(ICA模型)
Deep learning：三十二(基础知识_3)
Deep learning：三十一(数据预处理练习)
Deep learning：三十(关于数据预处理的相关技巧)
Deep learning：二十九(Sparse coding练习)
Deep learning：二十八(使用BP算法思想求解Sparse coding中矩阵范数导数)
Deep learning：二十七(Sparse coding中关于矩阵的范数求导)
Deep learning：二十六(Sparse coding简单理解)

Deep learning：十二(PCA和whitening在二自然图像中的练习) 
Deep learning：十一(PCA和whitening在二维数据中的练习) 
Deep learning：十(PCA和whitening)
Deep learning：九(Sparse Autoencoder练习)
Deep learning：八(Sparse Autoencoder)
outline

参考资料：

在此将降维相关的内容全部集中在本篇。

NB: 稀疏表达(sparse representation)和降维(dimensionality reduction)

Here, we should note that these two concepts are different! Remeber to distinguish! 

 

降维(dimensionality reduction)

十(PCA和whitening)

十二(PCA和whitening在二自然图像中的练习)

三十(关于数据预处理的相关技巧)

 

归一化 Data Normalization

数据的归一化一般包括

    • 样本尺度归一化，[kg, mm, ...]
    • 逐样本的均值相减，[brightness]
    • 特征的标准化。

 

数据尺度归一化的原因是：数据中每个维度表示的意义不同，所以有可能导致该维度的变化范围不同，因此有必要将他们都归一化到一个固定的范围，一般情况下是归一化到[0 1]或者[-1 1]。

这种数据归一化还有一个好处是对后续的一些默认参数（比如白化操作）不需要重新过大的更改。

逐样本的均值相减主要应用在那些具有稳定性的数据集中，也就是那些数据的每个维度间的统计性质是一样的。比如说，在自然图片中，这样就可以减小图片中亮度对数据的影响，因为我们一般很少用到亮度这个信息。不过逐样本的均值相减这只适用于一般的灰度图，在rgb等色彩图中，由于不同通道不具备统计性质相同性所以基本不会常用。

特征标准化是指对数据的每一维进行均值化和方差相等化。这在很多机器学习的算法中都非常重要，比如SVM等。

 

在使用PCA前需要对数据进行预处理，[This is 特征标准化]

    • 首先是均值化，即对每个特征维，都减掉该维的平均值，
    • 然后就是将不同维的数据范围归一化到同一范围，方法一般都是除以最大值。

但是比较奇怪的是，在对自然图像进行均值处理时并不是减去该维的平均值，而是减去这张图片本身的平均值。因为PCA的预处理是按照不同应用场合来定的。

 

Whitening

*Purpose

Whitening的目的是去掉数据之间的相关联度，是很多算法进行预处理的步骤。

比如说当训练图片数据时，由于图片中相邻像素值有一定的关联，所以很多信息是冗余的。这时候去相关的操作就可以采用白化操作。

*Before whitening

数据的whitening必须满足两个条件：

    • 一. 不同特征间相关性最小，接近0；[每一维独立]
    • 二. 所有特征的方差相等（不一定为1）。[每一维都除以标准差]

在对数据进行白化前要求先对数据进行特征零均值化，不过一般只要 我们做了(数据归一化)'s 特征标准化，那么这个条件必须就满足了。

*How to do whitening

在数据白化过程中，最主要的还是参数epsilon的选择，因为这个参数的选择对deep learning的结果起着至关重要的作用。

常见的白化操作有PCA whitening和ZCA whitening。

  • PCA whitening是指将数据x经过PCA降维为z后，可以看出z中每一维是独立的，满足whitening白化的第一个条件，这是只需要将z中的每一维都除以标准差就得到了每一维的方差为1，也就是说方差相等。公式为：

  • ZCA whitening是指数据x先经过PCA变换为z，但是并不降维，因为这里是把所有的成分都选进去了。这是也同样满足whtienning的第一个条件，特征间相互独立。然后同样进行方差为1的操作，最后将得到的矩阵左乘一个特征向量矩阵U即可。

ZCA whitening公式为：

 

Ref: 实现主成分分析和白化

--  参数epsilon的选择  --

为计算PCA白化后的数据 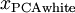\textstyle x_{\rm PCAwhite} ，可以用

xPCAwhite = diag(1./sqrt(diag(S) + epsilon)) * U' * x;

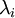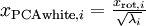因为 S 的对角线包括了特征值 \textstyle \lambda_i ，这其实就是同时为所有样本\textstyle i计算 \textstyle x_{{\rm PCAwhite},i} = \frac{x_{{\rm rot},i} }{\sqrt{\lambda_i}} 的简洁表达。

最后，你也可以这样计算ZCA白化后的数据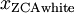\textstyle x_{\rm ZCAwhite}: 

xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;

 

在基于重构的模型中（比如说常见的RBM，Sparse coding, autoencoder都属于这一类，因为他们基本上都是重构输入数据），通常是选择一个适当的epsilon值使得能够对输入数据进行低通滤波。

但是何谓适当的epsilon呢？这还是很难掌握的，

    • epsilon太小，则起不到过滤效果，会引入很多噪声，而且基于重构的模型又要去拟合这些噪声；
    • epsilon太大，则又对元素数据有过大的模糊。

因此一般的方法是画出变化后数据的特征值分布图，如果那些小的特征值基本都接近0，则此时的epsilon是比较合理的。

如下图所示，让那个长长的尾巴接近于x轴。

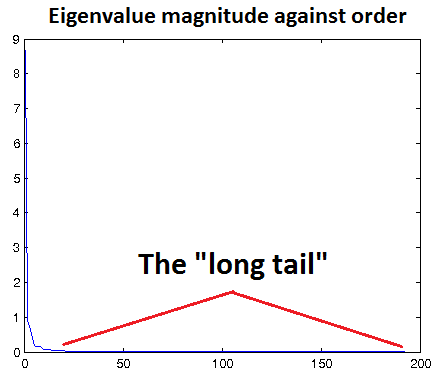
该图的横坐标表示的是第几个特征值，已经将数据集的特征值从大到小排序过。

文章中给出了个小小的实用技巧：

如果数据已被缩放到合理范围(如[0,1])，可以从epsilon = 0.01或epsilon = 0.1开始调节epsilon。

　　基于正交化的ICA模型中，应该保持参数epsilon尽量小，因为这类模型需要对学习到的特征做正交化，以解除不同维度之间的相关性。

 

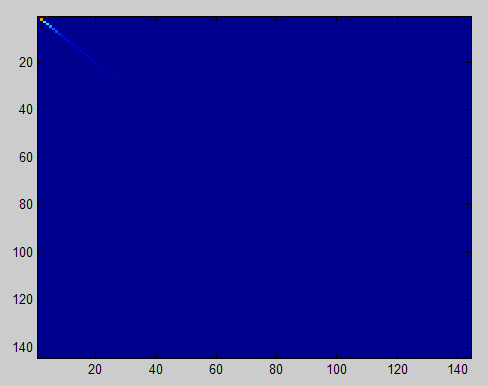
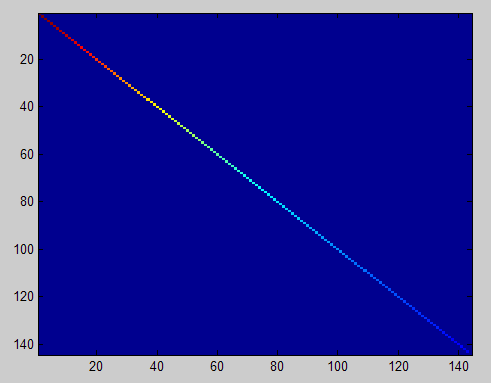
*Result:

Origianl photo --> left figure --> pca with 99% --> PCA Whitening --> 协方差矩阵 right figure

Thus, only main features remain after Whitening.

 

三十一(数据预处理练习)

Ref: http://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html

from sklearn.decomposition import PCA
pca = PCA(whiten=True)
pca.fit(X)

Replace with scikit api here.

 

三十三(ICA模型)

Goto: [Bayesian] “我是bayesian我怕谁”系列 - Continuous Latent Variables

 

 

八(Sparse Autoencoder)

九(Sparse Autoencoder练习)

十五(Self-Taught Learning练习) 

八、九主要还是稀疏约束部分，在稀疏表达中再详解。

十五就是效果等价于pca，降维而且识别率还高。

Self-taught learning or Semi-supervised learning 半监督学习

Self-taught learning是完全无监督的。

比如说我们需要设计一个系统来分类出轿车和摩托车。

    • 如果我们给出的训练样本图片是自然界中随便下载的（也就是说这些图片中可能有轿车和摩托车，有可能都没有，且大多数情况下是没有的），然后使用的是这些样本来特征模型的话，那么此时的方法就叫做self-taught learning。
    • 如果我们训练的样本图片都是轿车和摩托车的图片，只是我们不知道哪张图对应哪种车，也就是说没有标注，此时的方法不能叫做是严格的unsupervised feature，只能叫做是semi-supervised learning。

 


十六(deep networks)

该ML方法在特征提取方面是完全用的无监督方法，在上面的基础上再用有监督的方法继续对网络的参数进行微调，这样就可以得到更好的效果了。 

因为有了刚刚的初始化参数【等效pca的输入层的权重们】，此时的优化结果一般都能收敛到比较好的局部最优解

梯度扩散问题

先训练网络的第一个隐含层，然后接着训练第二个，第三个…最后用这些训练好的网络参数值作为整体网络参数的初始值。

前面的网络层次基本都用无监督的方法获得，只有最后一个输出层需要有监督的数据。

另外由于无监督学习其实隐形之中已经提供了一些输入数据的先验知识，所以此时的参数初始化值一般都能得到最终比较好的局部最优解。

最终还在于理解下面这个权重初始化的式子，从而防止梯度消失和爆炸。

 

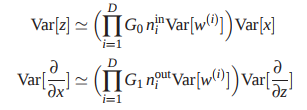
补充：stacked autoencoders - 比较常见的一种层次贪婪训练方法 【见下文详情】

单自动编码器，充其量也就是个强化补丁版PCA，只用一次好不过瘾。

于是Bengio等人在2007年的  Greedy Layer-Wise Training of Deep Networks 中，

仿照stacked RBM构成的DBN，提出Stacked AutoEncoder，为非监督学习在深度网络的应用又添了猛将。

 

 

十七(Linear Decoders，Convolution和Pooling)

convolution是为了解决前面无监督特征提取学习计算复杂度的问题；

pooling方法是为了后面有监督特征分类器学习的，也是为了减小需要训练的系统参数；

[ 当然这是在普遍例子中的理解，也就是说我们采用无监督的方法提取目标的特征，而采用有监督的方法来训练分类器 ]

 

假如对一张大图片Xlarge的数据集，r*c大小，则首先需要对这个数据集随机采样大小为a*b的小图片，然后用这些小图片patch进行学习（比如说sparse autoencoder），此时的隐含节点为k个。因此最终学习到的特征数为：

 　　

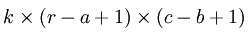
　　此时的convolution移动是有重叠的。

 

 

PCA Whitening是保证数据各维度的方差为1，而ZCA Whitening是保证数据各维度的方差相等即可，不一定要唯一。

并且这两种whitening的一般用途也不一样，PCA Whitening主要用于降维且去相关性，而ZCA Whitening主要用于去相关性，且尽量保持原数据。

因为目前tensorflow的出现，使用MATLAB的练习题貌似用处不大了。

stacked autoencoder貌似也没说什么，至于文中提到的反卷积显示问题，当下已经有了解决方案。

还有就是DBM可能是有必须学习stacked autoencoder的唯一理由了吧，毕竟随机初始化可以替代这些个繁琐的预处理过程。

 

 

二十(无监督特征学习中关于单层网络的分析)

二十一(随机初始化在无监督特征学习中的作用)

二十五(Kmeans单层网络识别性能)

一个隐含层的网络结构

本文是读Ng团队的论文” An Analysis of Single-Layer Networks in Unsupervised Feature Learning”后的分析，主要是针对一个隐含层的网络结构进行分析的。

分别对比了4种网络结构，k-means, sparse autoencoder, sparse rbm, gmm。

最后作者得出了下面几个结论：

1. 网络中隐含层神经元节点的个数，采集的密度（也就是convolution时的移动步伐）和感知区域大小对最终特征提取效果的影响很大，甚至比网络的层次数，deep learning学习算法本身还要重要。

2. Whitening在预处理过程中很有必要！

3. 在以上4种实验算法中，k-means效果竟然最好。因此在最后作者给出结论时的建议是，尽量使用whitening对数据进行预处理，每一层训练更多的特征数，采用更密集的方法对数据进行采样。 

【感知区域大小当前可通过””小卷积核+多层“来实现，这样参数少】

源于此论文：An Analysis of Single-Layer Networks in Unsupervised Feature Learning, Adam Coates, Honglak Lee, and Andrew Y. Ng. In AISTATS 14, 2011.

 

在On random weights and unsupervised feature learning. In ICML 2011,Saxe, A., Koh, P.W., Chen, Z., Bhand, M., Suresh, B., & Ng, A. (2011). 中又提出了个新观点：

即根本就无需通过那些复杂且消耗大量时间去训练网络的参数的deep learning算法，我们只需随机给网络赋一组参数值，其最终取得的特征好坏不比那些预训练和仔细调整后得到的效果些，而且这样还可以减少大量的训练时间。

 

 

当采用无监督的方法分层预训练深度网络的权值时，为了学习到较鲁棒的特征，可以在网络的可视层（即数据的输入层）引入随机噪声，

这种方法称为Denoise Autoencoder(简称dAE)，由Bengio在08年提出，见其文章Extracting and composing robust features with denoising autoencoders.

 

denoise后右图学习到的特征更具有代表性，给人印象深刻。右图同时也给人一种overfitting的感觉。

可见，特征这个东西，是越简单越好，表现出的样子就是右图所示。

 

 

四十八(Contractive AutoEncoder简单理解)

Contractive autoencoder是autoencoder的一个变种，其实就是在autoencoder上加入了一个规则项，它简称CAE。

  • 通常情况下，对权值进行惩罚后的autoencoder数学表达形式为：

 　　

  • CAE中，其数学表达式同样非常简单，如下：

 　　

　　 是隐含层输出值关于权重的雅克比矩阵，

 　　  表示的是该雅克比矩阵的F范数的平方，即雅克比矩阵中每个元素求平方

然后求和，更具体的数学表达式为：

 

关于雅克比矩阵的介绍可参考雅克比矩阵&行列式——单纯的矩阵和算子，

关于F范数可参考前面的博文Sparse coding中关于矩阵的范数求导中的内容。

有了loss函数的表达式，采用常见的mini-batch随机梯度下降法训练即可。

 

关于为什么contrative autoencoder效果这么好？

好的特征表示大致有2个衡量标准：

1. 可以很好的重构出输入数据;

2.对输入数据一定程度下的扰动具有不变形。

普通的autoencoder和sparse autoencoder主要是符合第一个标准。

deniose autoencoder和contractive autoencoder则主要体现在第二个，尤其是对于分类任务。

总之，Contractive autoencoder主要是抑制训练样本（处在低维流形曲面上）在所有方向上的扰动。

 

 

三十四(用NN实现数据的降维)

Goto: [UFLDL] Generative Model 【--> 重点反而不是降维，而是能量传播与全局最优】

 

稀疏表达(sparse representation)

 

posted @ 2017-11-16 19:40  郝壹贰叁  阅读(293)  评论(0)  编辑  收藏  举报