[Stats385] Lecture 01-02, warm up with some questions
Theories of Deep Learning
借该课程，进入战略要地的局部战斗中，采用红色字体表示值得深究的概念，以及想起的一些需要注意的地方。
Lecture 01
Lecture01: Deep Learning Challenge. Is There Theory? (Donoho/Monajemi/Papyan)
纯粹的简介，意义不大。
Lecture 02
Video: Stats385 - Theories of Deep Learning - David Donoho - Lecture 2
资料：http://deeplearning.net/reading-list/ 【有点意思的链接】
Readings for this lecture
1 A mathematical theory of deep convolutional neural networks for feature extraction
2 Energy propagation in deep convolutional neural networks
3 Discrete deep feature extraction: A theory and new architectures
4 Topology reduction in deep convolutional feature extraction networks
重要点记录：
未知概念：能量传播，Topology reduction
Lecturer said:
"Deep learning is simply an era where brute force has sudenly exploded its potential."
"How to use brute force (with limited scope) methold to yield result."
介绍ImageNet，没啥可说的；然后是基本back-propagation。
提了一句：
Newton法的发明人牛顿从来没想过用到NN这种地方，尬聊。
output的常见输出cost计算【补充】，介绍三种：
Assume z is the actual output and t is the target output.
| squared error: | E = (z-t)2/2 |
| cross entropy: | E = -t log(z) - (1-t)log(1-z) |
| softmax: | E = -(zi - log Σj exp(zj)), where i is the correct class. |
第一个难点：
严乐春大咖：http://yann.lecun.com/exdb/publis/pdf/lecun-88.pdf
通过拉格朗日不等式认识反向传播，摘自论文链接前言。
开始介绍常见的卷积网络模型以及对应引进的feature。
讲到在正则方面，dropout有等价ridge regression的效果。
通过这个对比：AlexNet vs. Olshausen and Field 引出了一些深度思考：
- Why does AlexNet learn filters similar to Olshausen/Field?
- Is there an implicit sparsity-promotion in training network?
- How would classification results change if replace learned filters in first layer with analytically defined wavelets, e.g. Gabors?
- Filters in the first layer are spatially localized, oriented and bandpass. What properties do filters in remaining layers satisfy?
- Can we derive mathematically?
Does this imply filters can be learned in unsupervised manner?
第三个难点：
关于卷积可视化，以及DeepDream的原理。
第四个难点：
补充一个难点：权重初始化的策略
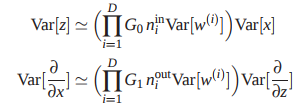
Links:
以上提及的重难点，未来将在此附上对应的博客链接。
