[Bayesian] “我是bayesian我怕谁”系列 - Markov and Hidden Markov Models
循序渐进的学习步骤是:
Markov Chain --> Hidden Markov Chain --> Kalman Filter --> Particle Filter
Markov不仅是一种技术,更是一种人生哲理,能启发我们很多。
一个信息爆炸的时代
一、信息的获取
首先要获得足够多的信息以及训练数据,才能保证所得信息中包含足够有价值的部分。但往往因为“面子”、“理子”、“懒"等原因,在有意无意间削弱了信息的获取能力。
二、信息的提取
信息中包含噪声,噪声中充斥着“有意无意善意恶意的谎言”、"或夸大或残缺的信息碎片”……HMM告诉我们获得“真实”,估计隐变量的必要性和理论依据。
三、信息的执行
在数据中提取出feature,获得了有价值的信息,但责任意识、执行力的薄弱往往又成为最后的障碍。
成功的人,在想尽办法获取足够多的信息,分析并提取有用部分,且能加以贯彻实践;
有些人,信息获取能力有限,信息提取能力有限,信息执行能力堪忧。
至少,隐马能唤醒大家对信息提取能力的重视;愿这一系列文章,有助于菜鸡的“信息获取”。
先做个广告,好书一本。

在此介绍一款形似GMM的产品:Mixture of Markov Chains。
物理意义可以理解为:不同的主题生成不同的句子 ---- 人说人话,鬼说鬼话。

前后单词会有概率关系,比如:
- “我爱” --> 以60%的几率后接 --> ”美__”;
- “我爱” --> 以1%的几率后接 --> ”丑__”。
马尔科夫链是个什么,这里不用多提。既然是“统计学习”,我们首要关注的还是上面这个PGM的边所代表的参数的估计,以及在估参过程中体会统计学习思维。至于模型的详细内容,一般会写在专题中,或在此文中提供亲测的资源链接。
这就是答案截图,为何一股EM的味道。
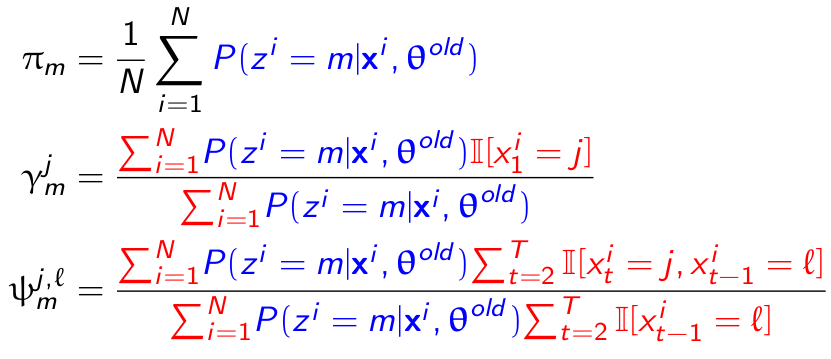
再谈EM:
但提到Markov Chains怎么也要考虑个二阶形式才感觉对味,加点难度何如。

粘贴second-order Markov Chains丑图一张
然.后.皆.是.套.路.
求我们的大Q。
发现参数θ又可以内部分离:pie与其他参数分离,可独立处理。

到这里,有点小麻烦,因为是二阶马尔科夫,每个节点的父节点有点多,参数表示也就麻烦了点儿。
参数的表示:
φ k = {φ 1 , φ 2 , ... φ D }, k ∈{1, 2, ... , Kz }
Here we add subscript for φ to denote that which z it belongs to, as following.
φ k = {φ k,1 , φ k,2 , ... φ k,D }

这张图充分体现了当年的自己是个整理狂,贴出来晒晒
这里继续对part2进行展开,便得到了接下来EM求导步骤的likelihood。
求导中用到了Lagrange Multiplier,当然,这也是套路的东西,你懂得。
机器学习中涉及的优化理论最多是凸优化,但凸优化其实是一大套很耐啃的理论,其中Lagrange Multiplier和Jensen's inequality的实用性尤甚。

在此附上结果,主要是用于对比一阶马尔科夫链时的结果,可见,形式是保持一致的。
参数有一坨,计算也繁复,但结果往往简洁漂亮。如果你有体会到这个感觉,恭喜,离坑更近了。
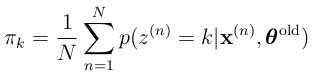



EM迭代公式
以上便是Mixture of Markov Chains,这里主要是换个模型展示EM,至于模型本身,不必留恋。
HMM
Ref: [Scikit-learn] Dynamic Bayesian Network - HMM
关于隐马,这部分对算法分类的概念有点乱,也可能是响应hmm”寻找真实状态“精神的号召,在大量的噪声中搞清楚内在逻辑。
因为篇幅有限,精力有限,这里不会写细节,但希望能把涉及到的概念理清楚,方便菜鸡们自行Google对应的详细讲解,毕竟,online资料有太多,这里仅帮助你搞清楚这些资料到底是在说什么。
建议大家把这些算法都亲自算一算,只能劝你到这里了。
基本概念:

Transition Distribution
Emission Distribution
Filtering: X1, X2, X3 -->Z3 【滤波,是个很宽泛的概念,可以理解为从噪声信息中提取出真实的部分】
Smoothing: X1, X2, X3 -->Z2
Prediction: X1, X2, X3 -->Z4
关于估参,We can use any standard inference method in graphical models to solve this problems, e.g. using the Junction Tree Algorithm.
读来如果对这句话仍感到困惑,则说明还未感知到PGM精髓。
迭代过程:
- Filtering

是个forward过程。
- Smoothing

有熟悉的forward过程,也有一个beta部分。
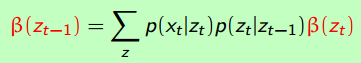
原来beta是个backward过程。
结合起来就是个forward-backward algorithm (or α − β recursions)
那么,这玩意干什么用?之后会提。
- Prediction
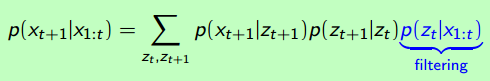
三大问题:
From: https://web.stanford.edu/~jurafsky/slp3/9.pdf

figure 1,三大问题
这里是常见的三大问题,上述也是经常会提及的迭代过程。那么,两者有什么关系?
这里涉及的一些概念的英文命名可能有些混乱,,你若有同感,推荐李航的《统计学习方法》


(1)
概率计算问题,对应figure 1中的 Problem 1 (likelihood),其实也叫evaluation问题。
理解要点:不同的状态序列可以产生一样的观测序列,那么所有情况的概率总和会是多少。
涉及到三个算法:
- 直接计算法【穷举所有可能的状态序列,显然很挫的手法】
- 前向算法(forward)
- 后向算法(backward)
现在再看forward-backward algorithm就明白了,也就是说,通过这些算法:
- 目前,我们主要是学习了如何计算:【观察值】的概率,【观察值】的likelihood,evaluation on 【观察值】!
- 然后通过贝叶斯公式,可以再计算:【状态值】的概率,【状态值】的likelihood,evaluation on 【状态值】!
一个问题:这里的状态值计算,指的是某个时间点的状态值,这是否保证了所有状态构成的状态链是最优的呢?也就是概率最大?
希望你能体会到这里我反复强调的苦心,一不留神,就容易迷失。
(2)
学习问题,自然就是”参数学习“,因为是统计机器学习,那么自然而然的又是em算法求参。
这里提到了两种情况:监督,无监督(Baum-Welch algorithm,也就是EM算法)。
- 前者就是,状态和观察都有了,求参 ---- 直觉看上去,也就是个统计起求bag of words的感觉,没什么意思。【李航 - 10.3.1节】
- 后者才是重点,毕竟状态就是label,哪有那么多资金去做标注,但我们却可以在无标注的情况下估计出一个近似的,可以接受的参数结果。
这部分学习内容,强烈建议:徐亦达机器学习课程 Hidden Markov Model;
不仅讲了Hidden Markov Chain,还有之后的Kalman Filter, Particle Filter。
重要的是,帮助你理清了这三者循序渐进的关系。
因为要强化理解em,也就是统计学习的套路,这里又列出”反复提及”的东西如下:
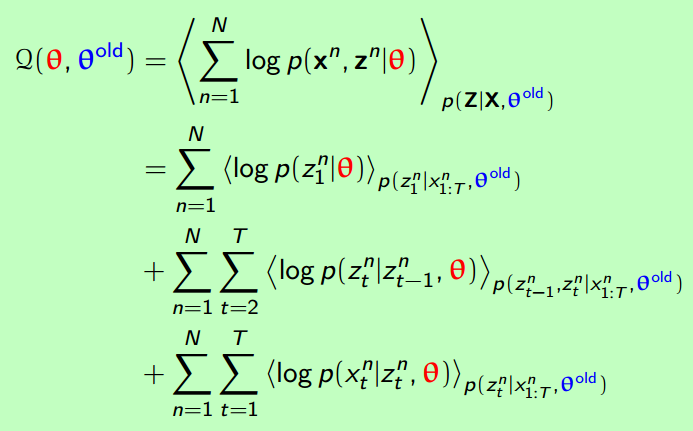
第一行是固定写法。
第二行写出具体形式,因为hmm公式在这里展开后比较清晰,故下一步将三部分各自求导得出迭代公式即可。
(3)
预测问题,呼应了前面的:Prediction: X1, X2, X3 -->Z4
这里还是回到【李航 - 10.4节】
Viterbi Algorithm求的是概率最大路径 based on 动态规划思想。想来也是如此,先保证过去整体状态链的判断是概率最大的,也就是某个算命先生的职业预测成功率是最高的,然后才敢请他预测下一个点。
而所谓的近似算法,也就是(1)概率计算问题中的“计算【状态值】的概率”的思维方式。当然,现在看来这个思维是有瑕疵的,解释如下:

读来有点”动态规划“批判”贪心算法“的口吻。
再看如下这三个单词,与三大问题的分类手法相比,其实就是视角不同而已。
这些是”过程式思维“,c语言;而“三大问题”是面向对象的思维,c++。
Filtering: X1, X2, X3 -->Z3
Smoothing: X1, X2, X3 -->Z2
Prediction: X1, X2, X3 -->Z4



 浙公网安备 33010602011771号
浙公网安备 33010602011771号