[Bayesian] “我是bayesian我怕谁”系列 - Continuous Latent Variables

写在前面

数据降维的几种形式

数据降维的几种方法，包括PCA、LDA、ICA等，另外还有一种常用的降维方法就是因子分析。

关于这几种方法的各自的优劣，有必要之后跟进一下。

 

概率图角度理解

打开prml and mlapp发现这部分目录编排有点小不同，但神奇的是章节序号竟然都为“十二”。

prml：pca --> ppca --> fa

mlapp：fa --> pca --> ppca

这背后又有怎样的隐情？不可告人的秘密又会隐藏多久？

 

基于先来后到原则，走prml路线。

首先，这部分内容，尤其是pca，都是老掉牙且稳定的技术，既然是统计机器学习，这次的目的就是借概率图来缕一遍思路，以及模型间的内在联系。

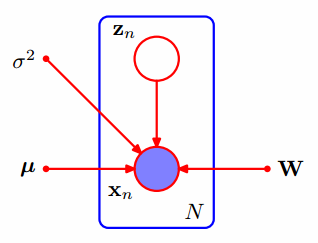
PPCA's PGM

我们要建立的是一套完整的知识体系，而非“拿来一用，用完就扔”的态度。

有菜鸡问了，为何你总是强调“体系”？

因为我是马刺队球迷。

 

首先，我希望大家重视prml的第12章开章这段话：

"本章中，我们⾸先介绍标准的、⾮概率的PCA⽅法，然后我们会说明，当求解线性⾼斯潜在变量模型的⼀种特别形式的最⼤似然解时， PCA如何⾃然地产⽣。这种概率形式的表⽰⽅法会带来很多好处，例如在参数估计时可以使⽤EM算法，对混合PCA模型的推广以及主成分的数量可以从数据中⾃动确定的贝叶斯公式。最后，我们简短地讨论潜在变量概念的几个推广，使得潜在变量的概念不局限于线性⾼斯假设。这种推广包括⾮⾼斯潜在变量，它引出了独⽴成分分析（ independent conponent analysis）的框架。这种推广还包括潜在变量与观测变量的关系是⾮线性关系的模型。"

 

因为大部分人都只关心以下这张图，也就是通过“映射”的角度来理解PCA。

然后，因为理解不全面，或者暂且只关心pca，对后面的部分就出现了理解断层。因为体系，波波维奇劝你要“站得高，看得远”。

 

 

PCA

有关pca的内容，网络资源有太多，以下个人链接能增加一点感性认识和相关内容；至于理性认识，除了动手亲自推倒公式，哪怕是抄一遍，也是极好的。

• • [Scikit-learn] 4.4 Dimensionality reduction - PCA
  • [Scikit-learn] 1.2 Dimensionality reduction - Linear and Quadratic Discriminant Analysis

因为pca+gmm常常是一个组合，先降维，去掉可能useless的信息，再进行gmm聚类。如此，至少能节省后期聚类时的计算资源。

其他没什么想说的，这个组合实践时确实效果蛮好，PCA也算是重要的预处理工具，数据预处理的地位你懂得，特征工程之百试不爽。 

 

 

PPCA

冒出一个“屁＋PCA”，恩，本来就挺好用，还要加个“P”？ —— 初次见面的初次感受。

PCA也可以被视为概率潜在变量模型的最⼤似然解。如何理解？

From: http://www.miketipping.com/papers/met-mppca.pdf【链接中x是隐变量】

公式推导

第一步：

先验：

似然：【原理见证明1，t = Wx+mu】

后验：

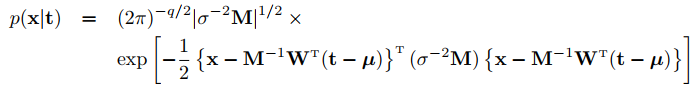
最后，期望就是最优解。

贝叶斯三部曲，没啥可说的，但这里有个Ｍ，如果假设σ²  = 0, 再带入结果，这不就是PCA麽。

 

第二步：

解的形式有了，但解中的变量是多少，比如W应该是多少呢？

通过mle获取，也就是获得Ｗ的估值。

(1)

联合分布，再积分掉x得t的边缘分布：

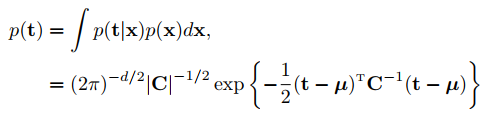
(2)

然后便获取了"t的似然"形式，如下：

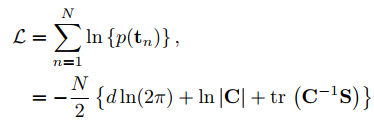
求导解似然方程就不再赘述here，过程详见链接。

答案中就包含了W的估值。读后感就是：一切皆是套路。

 

证明1

假设z是标准高斯，那么线性组合的每个x也是高斯。

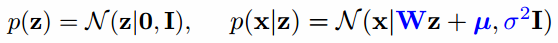
Figure, 证明１

这个证明看似很无聊，让我们思维大胆地扩展一下：

线性组合类似于没激活神经元的神经网络（NN）；因为有了激活函数，nn才能解决非线性问题。

但这里对应的貌似不是激活函数，而是概率。概率能否达到非线性的效果？为什么？

 

广义PCA

与传统的PCA相⽐，会带来一个本人感兴趣的优势就是，可以利用em高效求解。

好比用几何和代数解决同一个问题：用em总比“求解特征向量特征值”要划算的多，而且结果等价。当然还有其他优势，例如处理missing data。

 

此时，两个问题可能在菜鸡小脑中回荡：

• • • 不要问我mle方法中怎么涉及到了特征值计算，自己写一下Ｗ的估值瞧瞧。
    • 感觉似乎都搞完了啊，但怎么又涉及到了em？

读到这里，你如果有同样的疑惑，恭喜。好处便是，你不会感觉这系列文章的思维读来怪异，因为你我的脑回路可能是相通的。

因为mle在高维计算时没啥优势，所以考虑em。

这里看似是放弃了由mle得到的精确值，转而选择em带来的估计值，建议你想想，能提高内力心法。

因为FA就是ppca的方差扩展版本，所以，em的方法在fa中聊一次就好，节能。 

 

 

FA

cs229

既然是ppca的扩展，那么，咱就看看扩展ppca会发生什么？

 

首先，凭什么ppca的“先验”是标准高斯？改一改会如何？

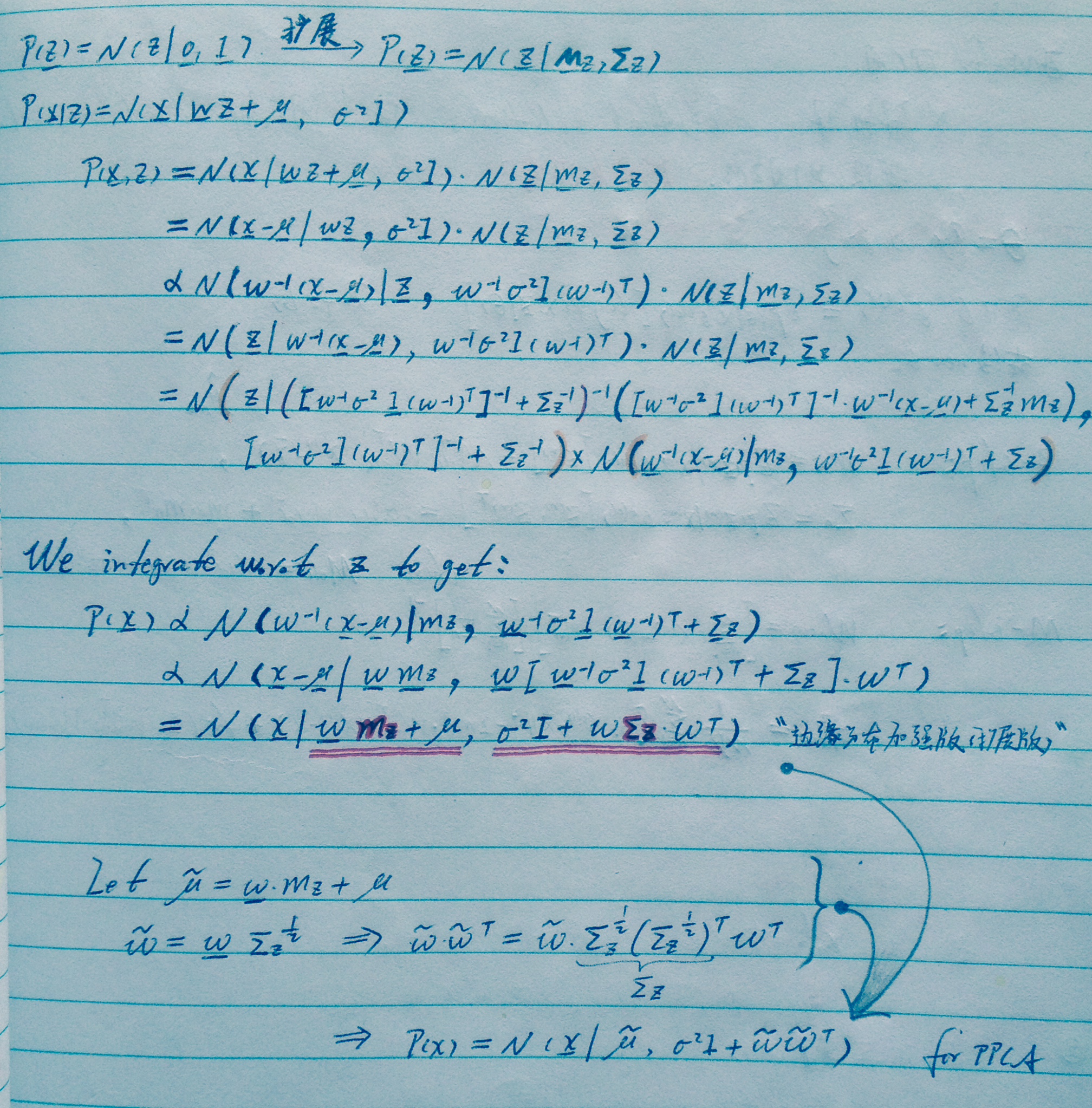
结论：x的边缘分布可以变为原来熟悉的样子。

 

扩展假设

按照fa的思路，凭什么x的边缘分布的方差是标准化的东东，改改会如何？

 

 

结论：不假设为“高斯”后，结果还是这个熟悉的形式。

可见，“龙生龙，凤生凤，老鼠的儿子会打洞”，高斯的衍生还是那么“高斯”。

 但问题是：边缘分布有点复杂，可见如下log likelihood。所以用em。

 

链接中用的Λ表示Ｗ，其他符号一致。

 

E step:

既然是em，E步骤计算：p(z⁽ⁱ⁾ | x⁽ⁱ⁾ ; µ, Λ, Ψ)

这里技巧在于，z和x都是高斯，一并构成了一个联合变量p(z, x)，这个东西通过p(z) * p(x|z)就可以求得。

那么P(z|x)就可以通过以下公式直接求得：

调整一下思维：

p(z), p(x|z), p(x)都有，本可以通过贝叶斯公式计算，但几个这么复杂的高斯除来除去，是个什么鬼？感觉也不好计算。

所以，先人给出了以上公式，通过联合概率就直接写出结果了。

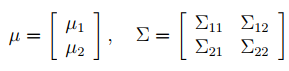
注意，联合概率是个高维高斯，且有两部分，一部分也可能包含多个维度。

 

Ｍ step:

思路就是通过log{P(x)}对各个参数求导。具体步骤，详见cs229链接，有超详细步骤，不再赘述。

 

先写到这里，本文只记录学习思路，帮助你建立知识体系，不会也不可能取代任何教材。

这一领域的东西，要充分领会，只能亲自动手算上一算。有时，你可能卡在一处无法进一步理解，该文可能会起到一点点“雪中送炭”的作用，这就足够了。

 

 

以上是通过PGM的角度去思考FA；下面是通过传统的方式去链接，详见链接。  

Ref: 因子分析(Factor Analysis)

 

 

FA能帮助我们做什么？

因子分析的过程其实是寻找共性因子和个性因子并得到最优解释的过程。 

因子分析有两个核心问题：一是如何构造因子变量，二是如何对因子变量进行命名解释。

 

与PCA的区别

因子分析经常与主成分分析（PCA）进行对比，以下是二者之间的异同点。

二者构造综合评价时所涉及的权数具有客观性，在原始信息损失不大的前提下，减少了后期数据挖掘和分析的工作量。

在处理的结果上都偏离了原有基于维度的认识，

• • PCA: 一个是基于变量的线性组合。
  • FA: 一个是基于因子的组合。 

 

主要区别

• • 原理不同。主成分分析的基本原理是利用降维（线性变换)的思想，在损失很少信息的前提下把多个指标转化为几个不相关的主成分，每个主成分都是原始变量的线性组合；
    而因子分析基本原理是从原始变量相关矩阵内部的依赖关系出发，把因子表达成能表示成少数公共因子和仅对某一个变量有作用的特殊因子的线性组合。（因子分析是主成分的推广，相对于主成分分析，更倾向于描述原始变量之间的相关关系）
  • 假设条件不同。主成分分析不需要有假设，而因子分析需要假设各个共同因子之间不相关，特殊因子（specificfactor）之间也不相关，共同因子和特殊因子之间也不相关。
  • 求解方法不同。主成分分析的求解方法从协方差阵出发，而因子分析的求解方法包括主成分法、主轴因子法、极大似然法、最小二乘法、a因子提取法等。
  • 降维后的“维度”数量不同，即因子数量和主成分的数量。主成分分析的数量最多等于维度数；而因子分析中的因子个数需要分析者指定（SPSS和SAS根据一定的条件自动设定，只要是特征值大于1的因子主可进入分析），指定的因子数量不同而结果也不同。

综合来看，因子分析在实现中可以使用旋转技术，因此可以得到更好的因子解释，这一点比主成分占优势；另外，因子分析不需要舍弃原有变量，而是站到原有变量间的共性因子作为下一步应用的前提，其实就是由表及里去发现内在规律。但是，主成分分析由于不需要假设条件，并且可以最大限度的保持原有变量的大多数特征，因此适用范围更广泛，尤其是宏观的未知数据的稳定度更高。

因子分析跟主成分分析一样，由于侧重点都是进行数据降维，因此很少单独使用，大多数情况下都会有一些模型组合使用。例如：

• 因子分析（主成分分析）+多元回归分析，判断并解决共线性问题之后进行回归预测；
• 因子分析（主成分分析）+聚类分析，通过降维后的数据进行聚类并分析数据特点，但因子分析会更适合，原因是基于因子的聚类结果更容易解释，而基于主成分的聚类结果很难解释。
• 因子分析（主成分分析）+分类，数据降维（或数据压缩）后进行分类预测，这也是常用的组合方法。

 

 

ICA

ICA也是该章节之内容，可见链接：[Scikit-learn] 2.5 Dimensionality reduction - ICA

其中推荐的几个链接写的不错，在此就不再赘述。但学习ICA的过程当中，希望菜鸡体会一个解决问题的过程：

1. 归纳问题
2. 选择测度方法

一个涉及到信息论的知识；一个则是测度论。

之前你若有读林达华有关machine learning需学习哪些数学科目的建议，其中便会提及这两个科目。

但人么，只有在实践中才能体会，ICA就是个很好的demo。对于年轻的菜鸡而言，体会信息论和测度论的价值与必要性，我认为远比ica本身要重要的多。 

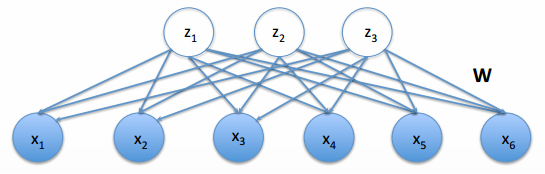
在此贴上此图，我希望菜鸡们能明白这么一个道理：

对于大部分自称机器学习的青年人而言，几乎都是从x₁到x₆这样的节点入手，表面看去确实是那么一回事，但节点之间却没有什么联系。

所谓建立知识体系，就是重视你的知识体系中隐变量的位置，“信息论”、“测度论”这些便是知识体系中的隐变量，至于其重要性，我想在看过这章节的内容后，你应该多少有点体会了吧。

这一系列的文章也不会对任何的observed variables大费口水，只会专注于唤醒你对latent variables的重视。

 

补充一个，在我看来非常有助于你认识概率图的例子。

本文起初的PCA也提到了通过传统方法，也就是通过“特征值”、“特征向量”的方式获得结果。

然后，通过概率的方式，具体得也就是PPCA的研究中发现也能推导出PCA的结论。

这个故事让你明白，研究一个东西可以从不同的视角，不同的视角思考的方式不同，理解难度也不同。

更重要的是，有些视角之间没有什么关系，这让每个概念的学习都成了独立的部分，你没有办法将学习经验迁移，无法模块化。

但概率图的视角，让你将pca，ppca，fa这些东西用统一的视角看去。其实，你若先学会了fa，再了解ppca，pca时，是否会很快呢？

 

再看ICA，史上最直白的ICA教程之一，不可否认这个链接挺不错，作者也很用心。但有没有更直白的方式？让我们来试一试：）

还是这幅图，想必你已经很熟悉。

z不再是高斯，但假设为另一个非高斯的iid先验分布。x是z的线性组合，所以x比z理论上会更“高斯”一些。

所以，为了x出现的概率最大，也就是mle，求出这些边所表示的参数（估参）。

估参时可以使用梯度下降逼近，或者一阶梯度，或者二阶梯度牛顿法。

有点小区别的是：这里的参数w属于：z = Wx

表述完毕，那么剩下的就是计算问题。如果你已对pca,ppca,fa了解，按照pgm的思维再瞧ica，so easy!

【学习迁移的能力，决定了你学习的速度，PGM就是这么一个神器】

 

最后，再看：

prml：pca --> ppca --> fa

mlapp：fa --> pca --> ppca

如写小说，一个循序渐进，一个倒叙法 罢了。

 

End.