[Scikit-learn] 2.1 Clustering - Variational Bayesian Gaussian Mixture
最重要的一点是：Bayesian GMM为什么拟合的更好？
PRML 这段文字做了解释：
Ref: http://freemind.pluskid.org/machine-learning/deciding-the-number-of-clusterings/
链接中提到了一些其他的无监督聚类。
From: http://scikit-learn.org/stable/modules/mixture.html#variational-bayesian-gaussian-mixture
Due to its Bayesian nature, the variational algorithm needs more hyper- parameters than expectation-maximization,
the most important of these being the concentration parameter weight_concentration_prior.
- Specifying a low value for the concentration prior will make the model put most of the weight on few components set the remaining components weights very close to zero.
- High values of the concentration prior will allow a larger number of components to be active in the mixture.
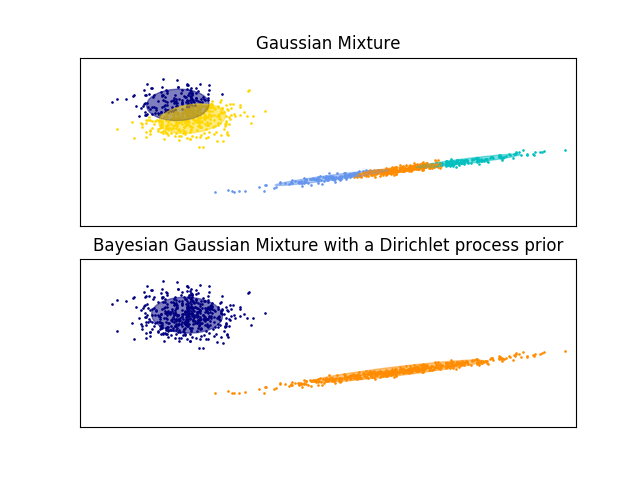
The examples below compare Gaussian mixture models with a fixed number of components, to the variational Gaussian mixture models with a Dirichlet process prior. Here, a classical Gaussian mixture is fitted with 5 components on a dataset composed of 2 clusters.
We can see that the variational Gaussian mixture with a Dirichlet process prior is able to limit itself to only 2 components whereas the Gaussian mixture fits the data with a fixed number of components that has to be set a priori by the user. In this case the user has selected n_components=5 which does not match the true generative distribution of this toy dataset. Note that with very little observations, the variational Gaussian mixture models with a Dirichlet process prior can take a conservative stand, and fit only one component.
Dirichlet distribution 具有自动的特征选取的作用，找出起主要作用的components。
5 for GMM
[ 0.1258077 0.23638361 0.23330578 0.26361639 0.14088652]
5 for Bayesian GMM
[ 0.001019 0.00101796 0.49948856 0.47955123 0.01892325]
问题来了：
为什么dirichlet会让三个的权重偏小，而GMM却没有，难道是收敛速度不同？
应该跟速度没有关系。加了先验后，后验变为了dirichlet，那么参数的估计过程中便具备了dirichlet的良好性质。
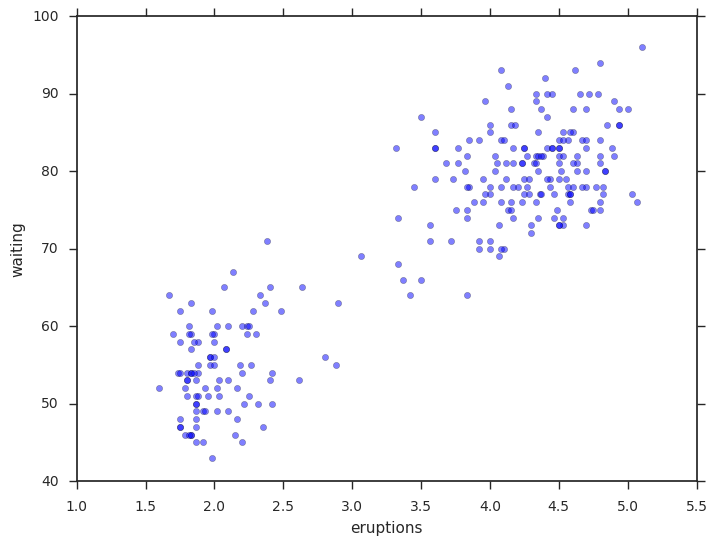
原始数据
Our data set will be the classic Old Faithful dataset.
plt.scatter(data['eruptions'], data['waiting'], alpha=0.5);
plt.xlabel('eruptions');
plt.ylabel('waiting');
如何拟合？
from sklearn.mixture import BayesianGaussianMixture
mixture_model = BayesianGaussianMixture(
n_components=10,
random_state=5, # control the pseudo-random initialization
weight_concentration_prior_type='dirichlet_distribution',
weight_concentration_prior=1.0, # parameter of the Dirichlet component prior
max_iter=200, # choose this to be big in case it takes a long time to fit
)
mixture_model.fit(data);
Ref: http://scikit-learn.org/stable/auto_examples/mixture/plot_concentration_prior.html
可直接调用该程式：
plot_ellipses(ax1, model.weights_, model.means_, model.covariances_)
def plot_ellipses(ax, weights, means, covars):
"""
Given a list of mixture component weights, means, and covariances,
plot ellipses to show the orientation and scale of the Gaussian mixture dispersal.
"""
for n in range(means.shape[0]):
eig_vals, eig_vecs = (covars[n])
unit_eig_vec = eig_vecs[0] / np.linalg.norm(eig_vecs[0])
angle = np.arctan2(unit_eig_vec[1], unit_eig_vec[0])
# Ellipse needs degrees
angle = 180 * angle / np.pi
# eigenvector normalization
eig_vals = 2 * np.sqrt(2) * np.sqrt(eig_vals)
ell = mpl.patches.Ellipse(
means[n], eig_vals[0], eig_vals[1],
180 + angle,
edgecolor=None,)
ell2 = mpl.patches.Ellipse(
means[n], eig_vals[0], eig_vals[1],
180 + angle,
edgecolor='black',
fill=False,
linewidth=1,)
ell.set_clip_box(ax.bbox)
ell2.set_clip_box(ax.bbox)
ell.set_alpha(weights[n])
ell.set_facecolor('#56B4E9')
ax.add_artist(ell)
ax.add_artist(ell2)
plot_results(
mixture_model,
data['eruptions'], data['waiting'],
'weight_concentration_prior={}'.format(1.0))
def plot_results(model, x, y, title, plot_title=False):
fig, ax = plt.subplots(3, 1, sharex=False)
# 上面是ax没用，以下重新定义了ax1 ax2
gs = gridspec.GridSpec(3, 1) # 自定义子图位置
ax1 = plt.subplot(gs[0:2, 0])
# 以下四行是固定套路
ax1.set_title(title)
ax1.scatter(x, y, s=5, marker='o', alpha=0.8)
ax1.set_xticks(())
ax1.set_yticks(())
n_components = model.get_params()['n_components']
plot_ellipses(ax1, model.weights_, model.means_, model.covariances_)
# ax1:画椭圆
# ax2:画权重
ax2 = plt.subplot(gs[2, 0])
ax2.get_xaxis().set_tick_params(direction='out')
ax2.yaxis.grid(True, alpha=0.7)
for k, w in enumerate(model.weights_):
ax2.bar(k, w, width=0.9, color='#56B4E9', zorder=3,
align='center', edgecolor='black')
ax2.text(k, w + 0.007, "%.1f%%" % (w * 100.),
horizontalalignment='center')
ax2.set_xlim(-.6, n_components - .4)
ax2.set_ylim(0., 1.1)
ax2.tick_params(axis='y', which='both', left='off',
right='off', labelleft='off')
ax2.tick_params(axis='x', which='both', top='off')
if plot_title:
ax1.set_ylabel('Estimated Mixtures')
ax2.set_ylabel('Weight of each component')
查看拟合过程：
lower_bounds = []
mixture_model = BayesianGaussianMixture(
n_components =10,
covariance_type ='full',
max_iter =1,
random_state =2,
weight_concentration_prior_type ='dirichlet_distribution',
warm_start =True,
)
# 设置model.fit为只递归一次
for i in range(200):
mixture_model.fit(data)
if mixture_model.converged_: break
lower_bounds.append(mixture_model.lower_bound_)
if i%5==0 and i<60:
plt.figure();
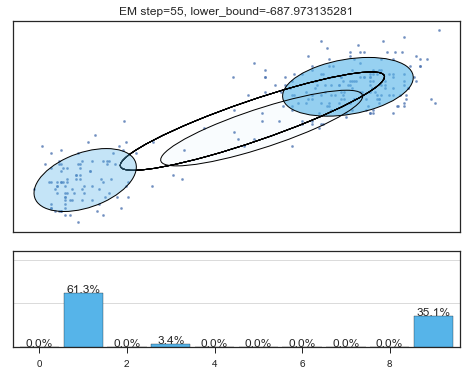
plot_results(
mixture_model,
data['eruptions'], data['waiting'],
'EM step={}, lower_bound={}'.format(
i, mixture_model.lower_bound_)
);
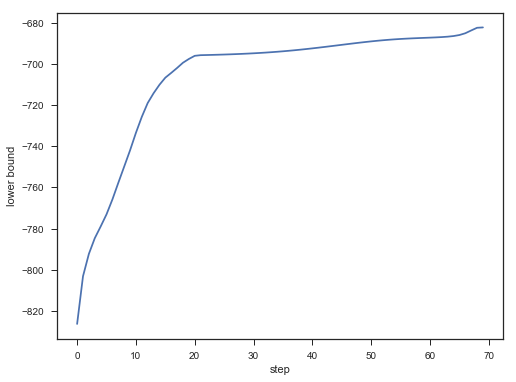
plt.figure();
plt.plot(lower_bounds);
plt.gca().set_xlabel('step')
plt.gca().set_ylabel('lower bound')
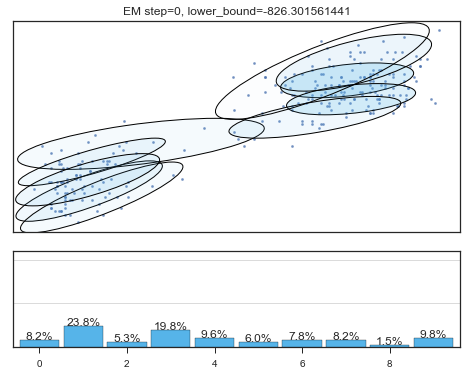
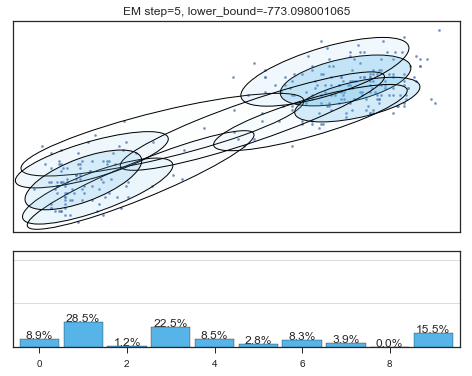
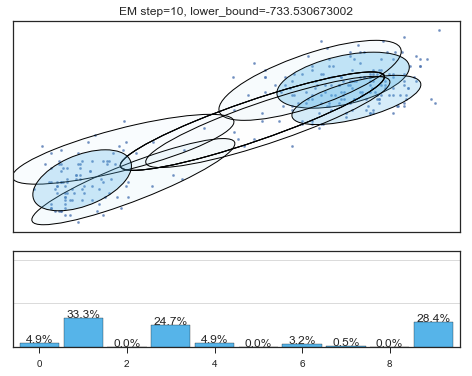
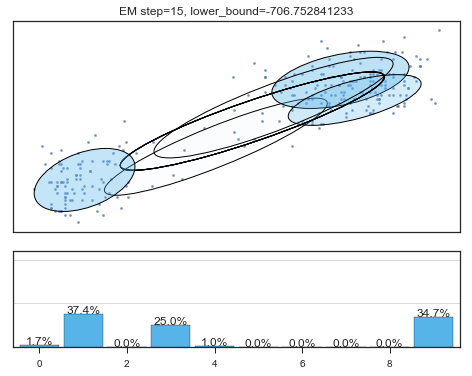
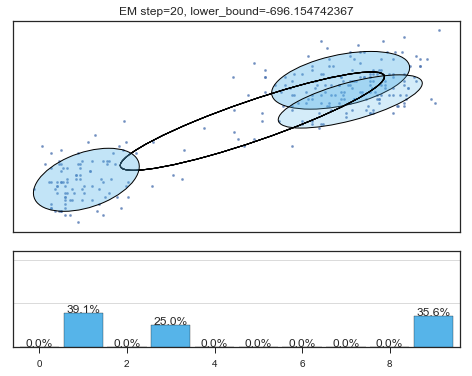
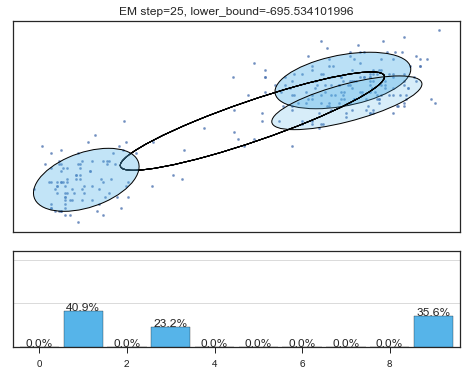
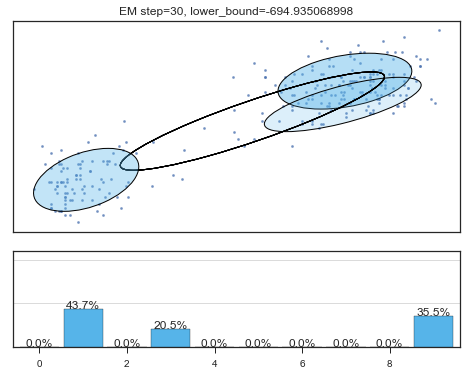
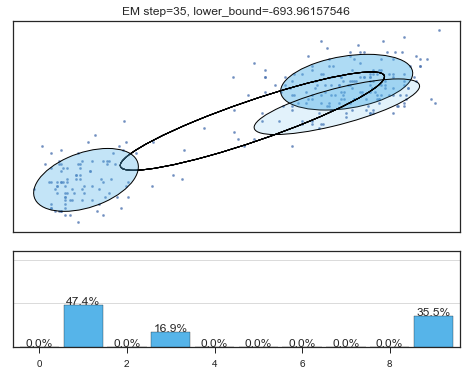
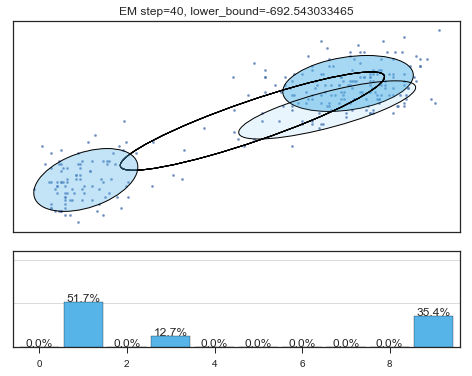
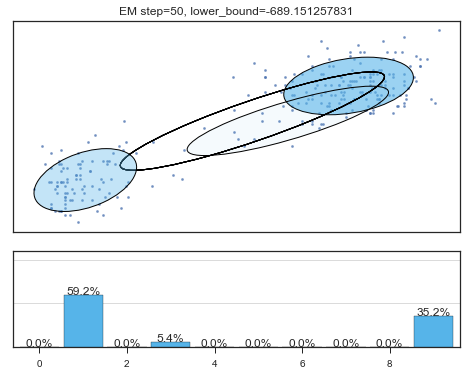
Lower bound 逐渐增加。
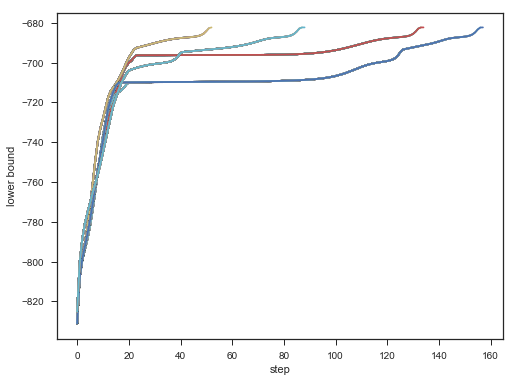
不同初始，效果对比：
for seed in range(6,11):
lower_bounds = []
mixture_model = BayesianGaussianMixture(
n_components=10,
covariance_type='full',
max_iter=1,
random_state=seed,
weight_concentration_prior_type='dirichlet_distribution',
warm_start=True,
)
for i in range(200):
mixture_model.fit(data)
if mixture_model.converged_: break
lower_bounds.append(mixture_model.lower_bound_)
plt.plot(lower_bounds);
plt.gca().set_xlabel('step')
plt.gca().set_ylabel('lower bound');
Result:
