[Scikit-learn] 4.4 Dimensionality reduction - PCA
2.5. Decomposing signals in components (matrix factorization problems)
- 2.5.1. Principal component analysis (PCA)
4.4. Unsupervised dimensionality reduction
- 4.4.1. PCA: principal component analysis
PCA+ICA 解混过程:https://www.zhihu.com/question/28845451
一、PCA的理解
PCA是将n维特征映射到k维上(k<n),这k维特征是全新的正交特征,称为主元,
是重新构造出来的k维特征,而不是简单的从n维特征中去除其余n-k维特征。
最大方差理论
From: https://www.zhihu.com/question/40043805/answer/138429562
既然牵涉到方差,自然联想到二乘法,即而自然联想到正态分布。
没错,PCA的基本假设是:数据集的分布是一个n维正态分布,并由此对协方差矩阵进行贝叶斯估计(其中期望这一参数被中心化消去了)。
你可以尝试写出这个贝叶斯分析中的概率似然函数,在假定协方差矩阵特征值一定的基础上,该似然函数的最大化形式就是PCA。
然而n维正态分布的协方差矩阵能不能被进一步简化呢?可以,一个自然而然简化矩阵的手段就是SVD。事实上对于一个n维正态分布的协方差矩阵作SVD和PCA是等价的。
不过PCA并不仅仅是巧合般利用了SVD,
-
- PCA的本质是对于一个以矩阵为参数的分布进行似然估计,
- SVD是矩阵近似的有效手段,仅此而已。
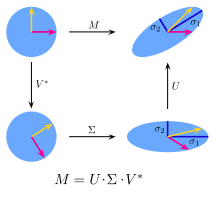
二、PCA的数学原理
Link: http://www.360doc.com/content/13/1124/02/9482_331688889.shtml
"发明一遍PCA"
(1). 基变换:旧坐标 --> 新坐标
单个坐标点
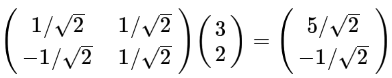
三个坐标点
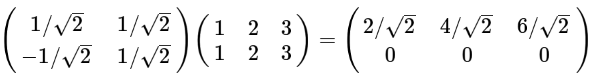
(2). 基的数量如果小于向量本身的维度
有两行,表示两个字段。
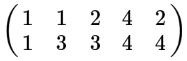
中心化后如下。

坐标表示。
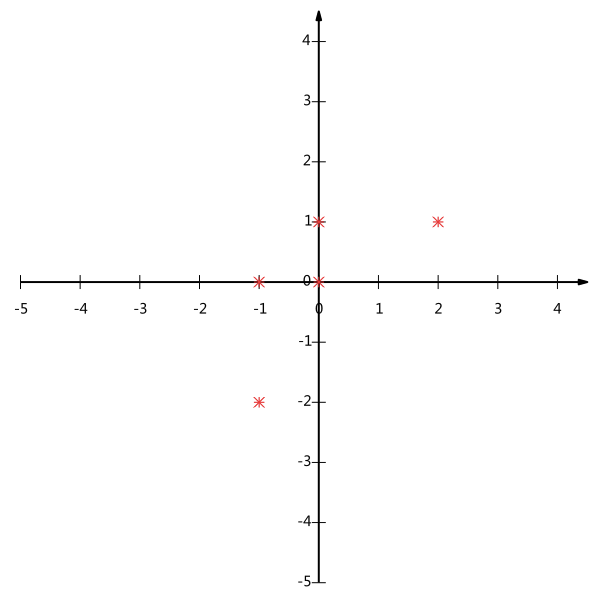
关键思想:降为一维后,希望投影后的投影值尽量的分散。
-
- 使用方差度量分散度。
- 两个字段的协方差表示其相关性。
正对角线:两个字段的反差
反对角线: 协方差

三、举个栗子
简单例子

对该数据进行PCA降维。

工程例子
Ref: Faces recognition example using eigenfaces and SVMs
通常就是pca + gmm or pca+svm的模式;降维后方便线性可分。
当然,主特征最好是天然正交的!
# #############################################################################
# Split into a training set and a test set using a stratified k fold
# split into a training and testing set
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.25, random_state=42)
# #############################################################################
# Compute a PCA (eigenfaces) on the face dataset (treated as unlabeled
# dataset): unsupervised feature extraction / dimensionality reduction
n_components = 150
print("Extracting the top %d eigenfaces from %d faces"
% (n_components, X_train.shape[0]))
t0 = time()
pca = PCA(n_components=n_components, svd_solver='randomized',
whiten=True).fit(X_train)
print("done in %0.3fs" % (time() - t0))
eigenfaces =pca.components_.reshape((n_components, h, w))
print("Projecting the input data on the eigenfaces orthonormal basis")
t0 = time()
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
print("done in %0.3fs" % (time() - t0))
# Jeff
print(pca.components_.shape)
print(eigenfaces.shape)
如下可见,协方差矩阵只有前150行被采用,作为了主特征。
pca.components_
类型:array,[n_components,n_features]
意义:特征空间中的主轴,表示数据中最大方差的方向。按explain_variance_排序。
Extracting the top 150 eigenfaces from 912 faces
done in 0.228s
Projecting the input data on the eigenfaces orthonormal basis
done in 0.024s
(150, 1850)
(150, 50, 37)
这些恐怖头像表示什么意思?

def plot_gallery(images, titles, h, w, n_row=3, n_col=4):
"""Helper function to plot a gallery of portraits"""
plt.figure(figsize=(1.8 * n_col, 2.4 * n_row))
plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.35)
for i in range(n_row * n_col):
plt.subplot(n_row, n_col, i + 1)
plt.imshow(images[i].reshape((h, w)), cmap=plt.cm.gray)
plt.title(titles[i], size=12)
plt.xticks(())
plt.yticks(())
4.4.1. PCA: principal component analysis 的内容,可进一步深入。
四、主特征选择
Ref: 选择主成分个数
我们该如何选择  ,即保留多少个PCA主成分?在上面这个简单的二维实验中,保留第一个成分看起来是自然的选择。对于高维数据来说,做这个决定就没那么简单:如果
,即保留多少个PCA主成分?在上面这个简单的二维实验中,保留第一个成分看起来是自然的选择。对于高维数据来说,做这个决定就没那么简单:如果  过大,数据压缩率不高,在极限情况
过大,数据压缩率不高,在极限情况 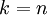 时,等于是在使用原始数据(只是旋转投射到了不同的基);相反地,如果
时,等于是在使用原始数据(只是旋转投射到了不同的基);相反地,如果  过小,那数据的近似误差太太。
过小,那数据的近似误差太太。
决定  值时,我们通常会考虑不同
值时,我们通常会考虑不同  值可保留的方差百分比。
值可保留的方差百分比。
具体来说,如果 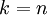 ,那么我们得到的是对数据的完美近似,也就是保留了100%的方差,即原始数据的所有变化都被保留下来;相反,如果
,那么我们得到的是对数据的完美近似,也就是保留了100%的方差,即原始数据的所有变化都被保留下来;相反,如果 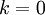 ,那等于是使用零向量来逼近输入数据,也就是只有0%的方差被保留下来。
,那等于是使用零向量来逼近输入数据,也就是只有0%的方差被保留下来。
一般而言,设 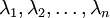 表示
表示 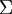 的特征值(按由大到小顺序排列),使得
的特征值(按由大到小顺序排列),使得 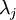 为对应于特征向量
为对应于特征向量 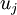 的特征值。那么如果我们保留前
的特征值。那么如果我们保留前  个成分,则保留的方差百分比可计算为:
个成分,则保留的方差百分比可计算为:
在上面简单的二维实验中,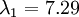 ,
,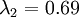 。因此,如果保留
。因此,如果保留 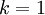 个主成分,等于我们保留了
个主成分,等于我们保留了 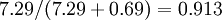 ,即91.3%的方差。
,即91.3%的方差。
对保留方差的百分比进行更正式的定义已超出了本教程的范围,但很容易证明,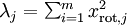 。因此,如果
。因此,如果 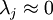 ,则说明
,则说明 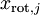 也就基本上接近于0,所以用0来近似它并不会产生多大损失。这也解释了为什么要保留前面的主成分(对应的
也就基本上接近于0,所以用0来近似它并不会产生多大损失。这也解释了为什么要保留前面的主成分(对应的 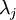 值较大)而不是末尾的那些。 这些前面的主成分
值较大)而不是末尾的那些。 这些前面的主成分 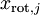 变化性更大,取值也更大,如果将其设为0势必引入较大的近似误差。
变化性更大,取值也更大,如果将其设为0势必引入较大的近似误差。
以处理图像数据为例,一个惯常的经验法则是选择  以保留99%的方差,换句话说,我们选取满足以下条件的最小
以保留99%的方差,换句话说,我们选取满足以下条件的最小  值:
值:
对其它应用,如不介意引入稍大的误差,有时也保留90-98%的方差范围。若向他人介绍PCA算法详情,告诉他们你选择的  保留了95%的方差,比告诉他们你保留了前120个(或任意某个数字)主成分更好理解。
保留了95%的方差,比告诉他们你保留了前120个(或任意某个数字)主成分更好理解。
五、Fisher Linear Discriminant Analysis (LDA)
补充:from http://blog.pluskid.org/?p=290
区分不同类别:[Scikit-learn] 1.2 Dimensionality reduction - Linear and Quadratic Discriminant Analysis
虽然 PCA 极力降低 reconstruction error ,试图得到可以代表原始数据的 components ,但是却无法保证这些 components 是有助于区分不同类别的。如果我们有训练数据的类别标签,则可以用 Fisher Linear Discriminant Analysis 来处理这个问题。
目的和作用
同 PCA 一样,Fisher Linear Discriminant Analysis 也是一个线性映射模型,只不过它的目标函数并不是 Variance 最大化,而是有针对性地使投影之后:
(1) 属于同一个类别的数据之间的 variance 最小化,
(2) 属于不同类别的数据之间的 variance 最大化。
具体的形式和推导可以参见《Pattern Classification》这本书的第三章 Component Analysis and Discriminants。
当然,很多时候(比如做聚类)我们并不知道原始数据是属于哪个类别的,此时 Linear Discriminant Analysis 就没有办法了。不过,如果我们假设原始的数据形式就是可区分的的话,则可以通过保持这种可区分度的方式来做降维。
MDS 是 PCA 之外的另一种经典的降维方法,它降维的限制就是要保持数据之间的相对距离。实际上 MDS 甚至不要求原始数据是处在一个何种空间中的,只要给出他们之间的相对“距离”,它就可以将其映射到一个低维欧氏空间中,通常是三维或者二维,用于做 visualization 。
End.



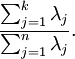

【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步