[PGM] Exact Inference for calculating marginal distribution
如何在贝叶斯网络中求解某变量的边缘分布?
这是一个问题。
贝叶斯网络如下:

CPTs如下:

(1) How to compute p( L | C = high )?
p( L | C = high )
= p(L, C=high) / p(C=high) // Bayesian Theorem.
= Joint dist / p(C=high) // 但是这里需要的却是joint dist!
求 Joint dist,便想到 变量消减,如下:
p( L, C)
= Σ ... Σ p(H) * p(L) * p(A) * p(V|H,L) * p(S|H,L) * p(C|V) * p(O|V,S) * p(B|O,T) * p(T|A) // 积分掉与L,C没任何关系的部分,加和=1
= ΣH ΣV p(H) * p(L) * p(V|H,L) * p(C|V) // 可见,结果只保留了与L,C有关的部分;因为H,V与L,C有牵扯,所以没法加和消减掉变量
= p(L) ΣV p(C|V) ΣH p(H) * p(V|H,L)
注意:消元的顺序不能胡来:
比如p(O|V,S)是可以最终消掉的,但O还作为了p(B|O,T)的条件部分,所以,
- 先消掉p(B|O,T) (如果B此时能消,也即是不在其他地方充当条件)
- 然后才能消O。
之后就是穷举V, H的过程。
先处理这一个部分:
ΣH p(H) * p(V|H,L) // 可见,除了H,剩余的两个变量(V,L)需要穷举所有离散情况,以便消减掉H
1. ΣH p(H) * p(V=low |H,L=true )
2. ΣH p(H) * p(V=high|H,L=true ) = 1 - ΣH p(H) * p(V=low|H,L=true ) // 求出1,即自动得出2
3. ΣH p(H) * p(V=low |H,L=false)
4. ΣH p(H) * p(V=high|H,L=false) = 1 - ΣH p(H) * p(V=low|H,L=false) // 求出3,即自动得出4
计算过程:
1. ΣH p(H) * p(V=low |H,L=true ) 等价于 p(V=low |L=true )
= p(H=true) * p(V=low|H=true,L=true) + p(H=false) * p(V=low |H=false,L=true) // 变为了可查表的形式
= 0.2 * 0.95 + 0.8 * 0.01
= 0.198
2. ΣH p(H) * p(V=high|H,L=true ) 等价于 p(V=high|L=true )
= 1 - ΣH p(H) * p(V=low|H,L=true )
= 1 - 0.198
= 0.802
3. ΣH p(H) * p(V=low |H,L=false) 等价于 p(V=low |L=false)
= p(H=true) * p(V=low|H=true,L=false) + p(H=false) * p(V=low |H=false,L=false) // 变为了可查表的形式
= 0.2 * 0.98 + 0.8 * 0.05
= 0.236
4. ΣH p(H) * p(V=high|H,L=false) 等价于 p(V=high|L=false)
= 1 - ΣH p(H) * p(V=low|H,L=false)
= 1 - 0.236
= 0.764
再处理剩下的部分:
p(L) * Σv p(C|V) * p(V|L) // 可见,除了V,剩余的两个变量(C,L)需要穷举所有离散情况,以便消减掉V
1. p(L=true ) * Σv p(C=high|V) * p(V|L=true )
2. p(L=false) * Σv p(C=high|V) * p(V|L=false) // 注意,Σv外有p(L),故不能直接采用补集的方法计算
计算过程:
1. p(L=true ) * Σv p(C=high|V) * p(V|L=true ) 等价于 p(L=true, C=high)
= p(L=true ) * p(C=high|V=low ) * p(V=low |L=true) + p(L=true ) * p(C=high|V=high) * p(V=high|L=true )
= 0.05 * 0.01 * 0.198 + 0.05 * 0.7 * 0.802
= 0.028169
2. p(L=false) * Σv p(C=high|V) * p(V|L=false) 等价于 p(L=false, C=high)
= p(L=false) * p(C=high|V=low ) * p(V=low |L=false) + p(L=false) * p(C=high|V=high) * p(V=high|L=false)
= 0.95 * 0.01 * 0.236 + 0.95 * 0.7 * 0.764
= 0.510302
Result:
p( L | C = high )
= p(L, C=high) / { p(C=high) } // Bayesian Theorem.
= p(L, C=high) / { p(L=true, C=high) + p(L=false, C=high) }
= p(L, C=high) / { 0.028169 + 0.510302 }
可见,结果就是Bernoulli distribution with probability with theta = 0.028169/(0.028169 + 0.510302)=0.052312938
(2) Then, compute p( L | C = high ) using the Junction Tree Algorithm.
1. Moralisation
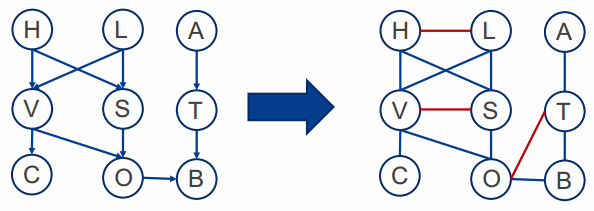
2. Triangulation
得到clique:{A, T}, {O,T,B}, {V, S,O}, {V, C}, {V, H, L, S}
3. Construction of the junction tree

4. Assignment of potentials
ψ(CV) = P(C|V) ψ(VSO) = P(O|V,S) ψ(VHLS) = P(V|H,L)P(S|H,L)P(H)P(L) ψ(OTB) = P(B|O,T) ψ(TA) = P(T|A)P(A)
Φ(V) = Φ(VS) = Φ(O) = Φ(T) = 1

根据以下算法更新evidence:


From left to right:
Φ(V) = 1
Φ*(V) = Σc ψ(CV) = Σc P(C|V) = P(C = high|V)
From right to left:
Φ(T) = 1
Φ*(T) = Σa ψ(TA) = Σa P(T|A)P(A) = P*(T)
ψ(OTB) = P(B|O,T)
ψ*(OTB) = ψ(OTB) x Φ*(T)/Φ(T) = ψ(OTB)
Φ(O) = 1
Φ*(O) = Σtb ψ(OTB) = Σtb P(B|O,T) = 1
ψ(VSO) = P(O|V,S)
ψ*(VSO) = ψ(VSO) x Φ*(O)/Φ(O) = ψ(VSO)
Φ(VS) = 1
Φ*(VS) = Σo ψ(VSO) = Σo P(O|V,S) = 1
更新 { V H L S }:
ψ*(VHLS)
= ψ(VHLS) x { Φ*(V) x Φ*(VS) } / { Φ(V) x Φ(VS) }
= P(V|H,L) * P(S|H,L) * P(H) * P(L) * { P(C = high|V) * 1 } / { 1 * 1 }
= P(V|H,L) * P(S|H,L) * P(H) * P(L) * P(C = high|V)

注意:我们当下已获得了置信传播的一个结果,就是 ψ*(VHLS),消息从左右两边都传递到了这里。
接下来,我们会如何用这个结果呢?这个结果又能给我们带来怎样的好处呢?
以下用于下一步的类比参考。
(1)用置信传播结果表示边缘条件概率
(2)头上加了小弯弯表示是已知变量,就是条件部分的变量。
照猫画虎就是如下:
p(L|C=high)
= p(L,C=high) / p(C=high) // Bayesian Theorem.
注意这里,分子分母的计算与传统方法比较时开始发生变化的地方,要体会。
已知:ψ*(VHLS)
分子:ΣVHS ψ*(VHLS)
分母:ΣVHSL ψ*(VHLS)
分母:(L这种情况下消不掉)
P(V|H,L) * P(S|H,L) * P(H) * P(L) * P(C = high|V)
变为:ΣVHL{ P(V|H,L) * P(H) * P(L) * P(C = high|V) }
分子:
P(V|H,L) * P(S|H,L) * P(H) * P(L) * P(C = high|V)
变为:ΣVH{ P(V|H,L) * P(H) * P(L) * P(C = high|V) }
可见,还是变为了穷举V,H的结果,最终也得到了方案(1)相同的结论。
后记:
这个例子可能不太完美,建议自己做一次P(O|H=true, L=true, A=true)。过程当中尤其体会对变量A的处理。
因为A是条件中的变量,所以在方法一中不能消去,这导致了计算资源的浪费;
在方法二中,就没有这个问题。好运。





