[BOOK] Applied Math and Machine Learning Basics
<Deep Learning>
- Ian Goodfellow
- Yoshua Bengio
- Aaron Courvill
关于此书Part One重难点的个人阅读笔记。
2.7 Eigendecomposition
we decompose a matrix into a set of eigenvectors and eigenvalues.
特征值与特征向量:
应用非常广泛:
图像处理中的PCA方法,选取特征值最高的k个特征向量来表示一个矩阵,从而达到降维分析+特征显示的方法,
还有图像压缩的K-L变换。
再比如很多人脸识别,数据流模式挖掘分析等方面。
在力学中,惯量的特征向量定义了刚体的主轴。惯量是决定刚体围绕质心转动的关键数据。
在谱系图论中,一个图的特征值定义为图的邻接矩阵A的特征值,或者(更多的是)图的拉普拉斯算子矩阵, Google的PageRank算法就是一个例子。
在量子力学中,特别是在原子物理和分子物理中,在Hartree-Fock理论下,原子轨道和分子轨道可以定义为Fock算子的特征向量。相应的特征值通过Koopmans定理可以解释为电离势能。在这个情况下,特征向量一词可以用于更广泛的意义,因为Fock算子显式地依赖于轨道和它们地特征值。
我曾经看到这么一句话:「有振动的地方就有特征值和特征向量」只要你真正理解了线性空间的矩阵的意义,你就明白了,几乎无处不在。
Youtube: https://www.youtube.com/watch?v=Qh3ObnbGtNc

A是对称的,那么扩展到一般情况就如2.8。
2.8 SVD
Ref: http://blog.csdn.net/wangran51/article/details/7408414
Link: https://www.youtube.com/watch?v=QLJp3gj_Qfk

提取出了本质。
举例:基于标签的推荐系统(隐语义模型)

代表减少了分类数。
详见:[IR] Concept Search and LSI
2.12 PCA
From: https://www.youtube.com/watch?v=0RWl5qEROic
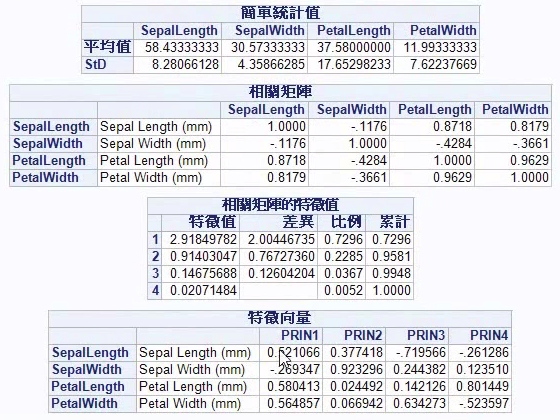
在统计学中,主成分分析(principal components analysis,PCA)是一种简化数据集的技术。它是一个线性变换。
这个变换把数据变换到一个新的坐标系统中,使得任何数据投影的
- 第一大方差在第一个坐标(称为第一主成分)上,
- 第二大方差在第二个坐标(第二主成分)上,
- 依次类推。
主成分分析经常用减少数据集的维数,同时保持数据集的对方差贡献最大的特征。
这是通过保留低阶主成分,忽略高阶主成分做到的。这样低阶成分往往能够保留住数据的最重要方面。但是,这也不是一定的,要视具体应用而定。
因为评估所涉及的众多变量之间既然有一定的相关性,就必然存在着起支配作用的因素。
根据这一点,通过对原始变量相关矩阵内部结构 的关系研究,找出影响科普效果某一要素的几个综合指标,使综合指标为原来变量的线性拟合。
这样,综合指标不仅保留了原始变量的主要信息,且彼此间不相关,又比原始变量具有某些更优越的性质,就使我们在研究复杂的科普效果评估问题时,容易抓住主要矛盾。
详见:[Scikit-learn] 4.4 Unsupervised dimensionality reduction
3.12 Technical Details of Continuous Variables
测度论 扩展了 概率论
测度论的一个重要贡献就是提供了一些集合的特征使得我们在计算概率时不会遇到悖论。
零测度:例如一根直线或一个点。
KL散度:衡量两个分布的差异。
交叉entropy:与KL密切相关,变分中也会用到这俩貌似。
4.2 病态条件
放大误差,对细小数敏感 是矩阵变换时的固有特性,我们也没有办法。
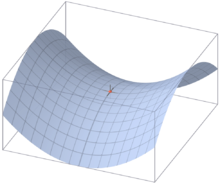
鞍点:一个不是局部极值点的驻点称为鞍点,例如:
4.3 基于梯度的优化方法
最速下降法(method of steepest descent)
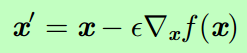
Jacobian Matrix
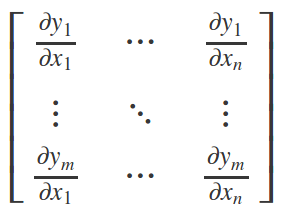
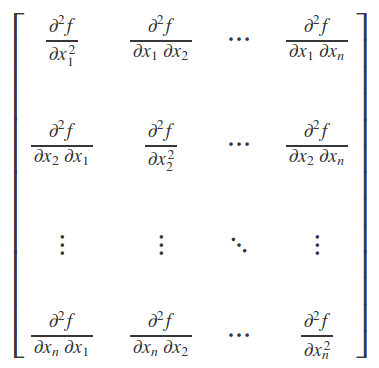
Hassian Matrix

Perhaps the most successful field of specialized optimization is convex optimization.
Convex optimization algorithms are able to provide many more guarantees by making stronger restrictions.
Convex optimization algorithms are applicable only to convex functions—functions for which the Hessian is positive semidefinite (半正定矩阵) everywhere.
Such functions are well-behaved because they lack saddle points and all of their local minima are necessarily global minima.
However, most problems in deep learning are difficult to express in terms of convex optimization.
Convex optimization is used only as a subroutine of some deep learning algorithms.
Ideas from the analysis of convex optimization algorithms can be useful for proving the convergence of deep learning algorithms.
However, in general, the importance of convex optimization is greatly diminished in the context of deep learning.
5.2 容量、过拟合和欠拟合
Vapnik Chervonenkis维 度量 二元分类器的容量,定义该分类器能够分类的训练样本的最大数目。
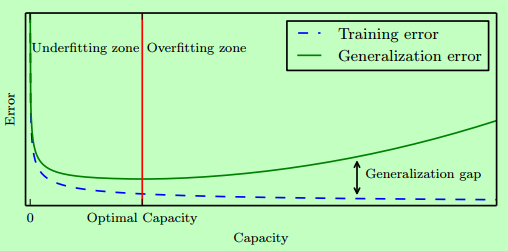
具体参见《台湾国立大学》的视频。
Ref: VC维的来龙去脉
5.11 挑战
平滑先验,局部不变性先验 (基本假设)
5.11.3 流形学习 (难)
专题 VC维的来龙去脉
历史
1943年,模拟神经网络由麦卡洛可(McCulloch)和皮茨(Pitts)提出,他们分析了理想化的人工神经元网络,并且指出了它们进行简单逻辑运算的机制。
1957年,康奈尔大学的实验心理学家弗兰克·罗森布拉特(Rosenblatt)在一台IBM–704计算机上模拟实现了一种他发明的叫作“感知机”(Perceptron)的神经网络模型。神经网络与支持向量机都源自于感知机(Perceptron)。
1962年,罗森布拉特著作:《神经动力学原理:感知机和大脑机制的理论》(Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms)。
1969年,明斯基和麻省理工学院的另一位教授佩普特合作著作:《感知机:计算几何学》(Perceptrons: An Introduction to Computational Geometry)。在书中,明斯基和佩普特证明单层神经网络不能解决XOR(异或)问题。
1971年,V. Vapnik and A. Chervonenkis在论文“On the uniform convergence of relative frequencies of events to their probabilities”中提出VC维的概念。
1974年,V. Vapnik提出了结构风险最小化原则。
1974年,沃波斯(Werbos)的博士论文证明了在神经网络多加一层,并且利用“后向传播”(Back-propagation)学习方法,可以解决XOR问题。那时正是神经网络研究的低谷,文章不合时宜。【学术潜规则】
1982年,在加州理工担任生物物理教授的霍普菲尔德,提出了一种新的神经网络,可以解决一大类模式识别问题,还可以给出一类组合优化问题的近似解。这种神经网络模型后被称为霍普菲尔德(Hopfield)网络。
1986年,Rummelhart与McClelland发明了神经网络的学习算法Back Propagation。
1993年,Corinna Cortes和Vapnik等人提出了支持向量机(support vector machine)。神经网络是多层的非线性模型,支持向量机利用核技巧把非线性问题转换成线性问题。
1992~2005年,SVM与Neural network之争,但被互联网风潮掩盖住了。
2006年,Hinton提出神经网络的Deep Learning算法。Deep Learning假设神经网络是多层的,首先用Restricted Boltzmann Machine(非监督学习)学习网络的结构,然后再通过Back Propagation(监督学习)学习网络的权值。
现在,deep learning的应用越来越广泛,甚至已经有超越SVM的趋势。一方面以Hinton,Lecun为首的深度学习派坚信其有效实用性,另一方面Vapnik等统计机器学习理论专家又坚持着理论阵地,怀疑deep learning的泛化界。
【一直觉得,这段历史足以拍成一部奥斯卡电影】
中间部分详见原文。
深度学习与VC维
对于神经网络,其VC维的公式为:
dVC = O(VD),其中V表示神经网络中神经元的个数,D表示weight的个数,也就是神经元之间连接的数目。(注意:此式是一个较粗略的估计,深度神经网络目前没有明确的vc bound)
举例来说,一个普通的三层全连接神经网络:input layer是1000维,hidden layer有1000个nodes,output layer为1个node,则它的VC维大约为O(1000*1000*1000)。
可以看到,神经网络的VC维相对较高,因而它的表达能力非常强,可以用来处理任何复杂的分类问题。
根据上一节的结论,要充分训练该神经网络,所需样本量为10倍的VC维。
如此大的训练数据量,是不可能达到的。所以在20世纪,复杂神经网络模型在out of sample的表现不是很好,容易overfit。
但现在为什么深度学习的表现越来越好。原因是多方面的,主要体现在:
- 通过修改神经网络模型的结构,以及提出新的regularization方法,使得神经网络模型的VC维相对减小了。例如卷积神经网络,通过修改模型结构(局部感受野和权值共享),减少了参数个数,降低了VC维。2012年的AlexNet,8层网络,参数个数只有60M;而2014年的GoogLeNet,22层网络,参数个数只有7M。再例如dropout,drop connect,denosing等regularization方法的提出,也一定程度上增加了神经网络的泛化能力。
- 训练数据变多了。随着互联网的越来越普及,相比于以前,训练数据的获取容易程度以及量和质都大大提升了。训练数据越多,Ein越容易接近于Eout。而且目前训练神经网络,还会用到很多data augmentation方法,例如在图像上,剪裁,平移,旋转,调亮度,调饱和度,调对比度等都使用上了。
- 除此外,pre-training方法的提出,GPU的利用,都促进了深度学习。
但即便这样,深度学习的VC维和VC Bound依旧很大,其泛化控制方法依然没有强理论支撑。但是实践又一次次证明,深度学习是好用的。所以VC维对深度学习的指导意义,目前不好表述,有一种思想建议,深度学习应该抛弃对VC维之类概念的迷信,尝试从其他方面来解释其可学习型,例如使用泛函空间(如Banach Space)中的概率论。
补充:
Lagrange Multiplier and KKT in GMM
Ref: [Scikit-learn] 2.1 Gaussian mixture models & EM
拉格朗日乘子法(Lagrange Multiplier) 和KKT条件
在求取有约束条件的优化问题时,拉格朗日乘子法(Lagrange Multiplier) 和KKT条件是非常重要的两个求取方法,
-
- 对于等式约束的优化问题,可以应用拉格朗日乘子法去求取最优值;
- 如果含有不等式约束,可以应用KKT条件去求取。
当然,这两个方法求得的结果只是必要条件,只有当是凸函数的情况下,才能保证是充分必要条件。
KKT条件是拉格朗日乘子法的泛化。
之前学习的时候,只知道直接应用两个方法,但是却不知道为什么拉格朗日乘子法(Lagrange Multiplier) 和KKT条件能够起作用,为什么要这样去求取最优值呢?
继续中。。。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号