[Bayes] Multinomials and Dirichlet distribution
From: https://www.cs.cmu.edu/~scohen/psnlp-lecture6.pdf 不错的PPT,图示很好。
伯努利分布 和 多项式分布
Binomial Distribution的共轭先验Beta Distribution。
贝塔分布的范围符合色子的每一面的概率理解。

同理:
Multinomials Distribution的共轭先验Dirichlet Distribution。
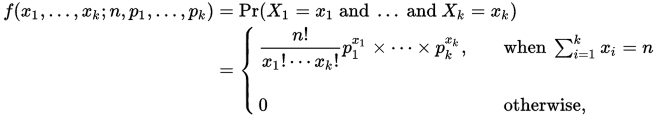
Ref: https://docs.scipy.org/doc/numpy/reference/generated/numpy.random.multinomial.html
>>> np.random.multinomial(20, [1/6.]*6, size=2) # 做size=2次实验,一次是20次抛投
array([[3, 4, 3, 3, 4, 3], # 第一次实验的结果:第一面出现了3次,第二面出现了4次,etc.
[2, 4, 3, 4, 0, 7]]) # 第二次实验同理。
没法做图表示,维度太高了,大于了三维。第三维要留下来表示Pr。
狄利克雷分布:
Dirichlet分布可以看做是分布之上的分布。如何理解这句话,我们可以先举个例子:
- 假设我们有一个骰子,其有六面,分别为{1,2,3,4,5,6}。现在我们做了10000次投掷的实验,得到的实验结果是六面分别出现了{2000,2000,2000,2000,1000,1000}次,如果用每一面出现的次数与试验总数的比值估计这个面出现的概率,则我们得到六面出现的概率,分别为{0.2,0.2,0.2,0.2,0.1,0.1}。
- 我们想要做10000次试验,每次试验中我们都投掷骰子10000次。我们想知道,出现这样的情况使得我们认为,骰子六面出现概率为{0.2,0.2,0.2,0.2,0.1,0.1}的概率是多少(说不定下次试验统计得到的概率为{0.1, 0.1, 0.2, 0.2, 0.2, 0.2}这样了)。
这样我们就在思考骰子六面出现概率分布这样的分布之上的分布。
而这样一个分布就是Dirichlet分布。

- xi 代表每一面的概率。
- 阿尔法是参数向量。
- 以下B函数是为了归一化!
- 可以看出,每一个结果:(x1, x2... xn)都会相应地给出一个概率!

伽玛函数(Gamma函数),也叫欧拉第二积分,是阶乘函数在实数与复数上扩展的一类函数。
与之有密切联系的函数是贝塔函数(Beta函数),也叫第一类欧拉积分。可以用来快速计算同伽马函数形式相类似的积分。

长得比较诡异。
Ref: https://docs.scipy.org/doc/numpy/reference/generated/numpy.random.dirichlet.html
一个三维的向量,随机抽取一个。每一维代表一个面的概率。
>>> s = np.random.dirichlet((10, 5, 3), 20) >>> s array([[ 0.52347182, 0.44608268, 0.0304455 ], [ 0.55583862, 0.35281005, 0.09135134], [ 0.49311777, 0.32315067, 0.18373157], [ 0.70968695, 0.22268722, 0.06762583], [ 0.60323203, 0.26006693, 0.13670104], [ 0.69403583, 0.21325088, 0.09271329], [ 0.53413248, 0.23281167, 0.23305585], [ 0.62858314, 0.18519664, 0.18622022], [ 0.52497339, 0.20176998, 0.27325663], [ 0.47283724, 0.39204232, 0.13512045], [ 0.66621238, 0.24627779, 0.08750983], [ 0.43605494, 0.46696468, 0.09698038], [ 0.41539035, 0.37153284, 0.21307682], [ 0.85737303, 0.11670994, 0.02591703], [ 0.53161652, 0.28426861, 0.18411488], [ 0.55155807, 0.16826288, 0.28017905], [ 0.45716724, 0.33973818, 0.20309457], [ 0.45320309, 0.26896615, 0.27783076], [ 0.80522192, 0.10022979, 0.09454829], [ 0.45790405, 0.42998929, 0.11210666]])
可见,参数某个比较大时,会出现一个高的相对稳定的概率峰值。
>>> s = np.random.dirichlet((10, 1, 1), 20)
>>> s
array([[ 0.8557684 , 0.09807372, 0.04615788],
[ 0.83456424, 0.03670665, 0.12872911],
[ 0.73520196, 0.2017358 , 0.06306224],
[ 0.73759042, 0.18157695, 0.08083263],
[ 0.89338746, 0.00237974, 0.1042328 ],
[ 0.93393029, 0.01373741, 0.0523323 ],
[ 0.96453549, 0.02562915, 0.00983536],
[ 0.90688036, 0.02557378, 0.06754587],
[ 0.96455728, 0.02084742, 0.01459531],
[ 0.82136655, 0.07921894, 0.09941451],
[ 0.78585535, 0.00286702, 0.21127763],
[ 0.91597604, 0.0276861 , 0.05633787],
[ 0.90984927, 0.04313451, 0.04701622],
[ 0.81386422, 0.08610383, 0.10003195],
[ 0.92675313, 0.06861093, 0.00463594],
[ 0.98362761, 0.00299704, 0.01337535],
[ 0.90807198, 0.02043488, 0.07149314],
[ 0.90418455, 0.07209613, 0.02371932],
[ 0.9630694 , 0.00459631, 0.03233429],
[ 0.65105053, 0.05350025, 0.29544922]])
阿尔法和小一点,则less peaked:出现了些许不稳定,某一个Pr的垄断性不是特别强。
>>> s = np.random.dirichlet((5, 1, 1), 20)
>>> s
array([[ 0.7373676 , 0.17431797, 0.08831443],
[ 0.8022481 , 0.02474368, 0.17300822],
[ 0.90968516, 0.06022567, 0.03008917],
[ 0.9011515 , 0.02337192, 0.07547658],
[ 0.98846934, 0.00932316, 0.0022075 ],
[ 0.66322211, 0.24058232, 0.09619557],
[ 0.86661876, 0.0542239 , 0.07915735],
[ 0.48498043, 0.25048716, 0.26453241],
[ 0.79705359, 0.16538074, 0.03756567],
[ 0.68670999, 0.17210651, 0.1411835 ],
[ 0.65227745, 0.20477286, 0.1429497 ],
[ 0.73701086, 0.15733187, 0.10565728],
[ 0.68017492, 0.04459314, 0.27523195],
[ 0.50579841, 0.42922063, 0.06498096],
[ 0.71188347, 0.13582756, 0.15228897],
[ 0.69952146, 0.08344366, 0.21703488],
[ 0.39333132, 0.49440346, 0.11226522],
[ 0.47531785, 0.21319548, 0.31148667],
[ 0.67575678, 0.25481807, 0.06942515],
[ 0.83958139, 0.08429426, 0.07612435]])
共轭,得到后验如下:




