[Bayes] Metroplis Algorithm --> Gibbs Sampling
重要的是Gibbs的思想。
全概率分布,可以唯一地确定一个联合分布 ---- Hammersley-Clifford
多元高斯分布
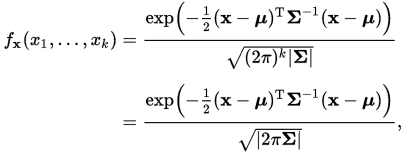
当然,这个有点复杂,考虑个简单的,二元高斯,那么超参数就是:
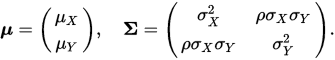
二元高斯联合分布:

将其中一个作为已知常数,也就是求条件分布,正好就体现了Gibbs的特性:

#initialize constants and parameters
N <- 5000 #length of chain
burn <- 1000 #burn-in length
X <- matrix(0, N, 2) #the chain, a bivariate sample
rho <- -.75 #correlation
mu1 <- 0
mu2 <- 2
sigma1 <- 1
sigma2 <- .5
s1 <- sqrt(1-rho^2)*sigma1
s2 <- sqrt(1-rho^2)*sigma2
###### generate the chain #####
X[1, ] <- c(mu1, mu2) #initialize
for (i in 2:N) {
x2 <- X[i-1, 2]
m1 <- mu1 + rho * (x2 - mu2) * sigma1/sigma2
X[i, 1] <- rnorm(1, m1, s1)
x1 <- X[i, 1]
m2 <- mu2 + rho * (x1 - mu1) * sigma2/sigma1
X[i, 2] <- rnorm(1, m2, s2)
}
b <- burn + 1
x <- X[b:N, ]
# compare sample statistics to parameters
colMeans(x)
cov(x)
cor(x)
plot(x, main="", cex=.5, xlab=bquote(X[1]),
ylab=bquote(X[2]), ylim=range(x[,2]))
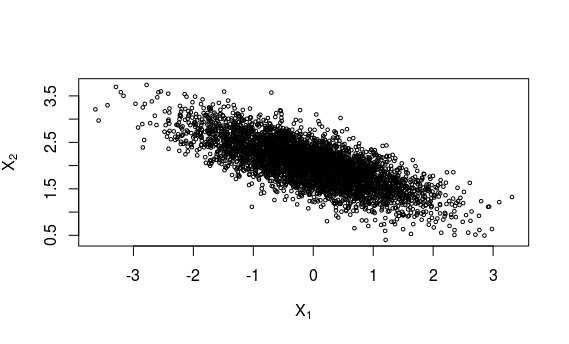
采样结果:





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步