[Optimization] Dynamic programming
“就是迭代,被众人说得这么玄乎"
“之所以归为优化,是因为动态规划本质是一个systemetic bruce force"
“因为systemetic,所以比穷举好了许多,就认为是优化的功绩咯"

一个热身问题
不等长活动的安排
活动不等长,安排利用率最高的活动安排。
不同于“贪心算法”的例子,这里希望活动地点的时间利用率尽量的满,而不是“为满足更多的活动”。

三个例子:
T(1) = f1-s1
T(2) = f2-s2
T(3) = T(1) + f3-s3,包含了子问题T(1);
核心思维:
T(3)时,就要优先保留住f3-s3,然后再看其他"不冲突的items";这些"不冲突的items"其实是个之前的子问题。

T(n) 不一定是最大,所以,最后要找出Table中的T(1)->T(n)中最大的,即是最优的。
进化而来的 "动态规划"
最长公共子序列法 (LCS)
寻找子问题的思想
Ref: http://www.cnblogs.com/liyukuneed/archive/2013/05/22/3090597.html
动态规划,众所周知,第一步就是找子问题,也就是把一个大的问题分解成子问题。
A = "a0, a1, a2, ..., am-1",
B = "b0, b1, b2, ..., bn-1"。
如果am-1 == bn-1,则当前最长公共子序列为"a0, a1, ..., am-2"与"b0, b1, ..., bn-2"的最长公共子序列与am-1的和。长度为"a0, a1, ..., am-2"与"b0, b1, ..., bn-2"的最长公共子序列的长度+1。
// 尾巴一样,那肯定可以直接考虑“子问题”;
如果am-1 != bn-1,则最长公共子序列为max("a0, a1, ..., am-2"与"b0, b1, ..., bn-1"的公共子序列,"a0, a1, ..., am-1"与"b0, b1, ..., bn-2"的公共子序列)
// 尾巴如果不一样,你的尾巴可能是我的倒数第二个;我的尾巴也可能是你的倒数第二个;二者找一个最大的就好;
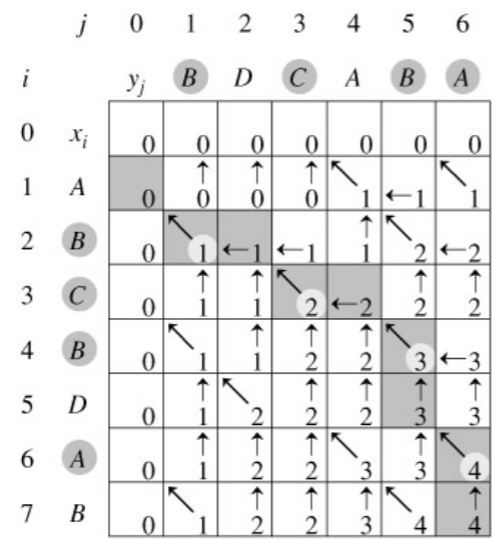
可视化为“二维数组”
按照动态规划的思想,对问题的求解,其实就是对子问题自底向上的计算过程。
这里,计算c[i][j]时,c[i-1][j-1]、c[i-1][j]、c[i][j-1]已经计算出来了,这样,我们可以根据X[i]与Y[j]的取值,按照上面的递推,求出c[i][j],同时把路径记录在b[i][j]中(路径只有3中方向:左上、左、上,如下图)。
最长递增子序列(LIS)
Ref: 最长递增子序列
给定一个长度为N的数组,找出一个最长的单调自增子序列(不一定连续,但是顺序不能乱)。
例如:
给定一个长度为6的数组A{5, 6, 7, 1, 2, 8},则其最长的单调递增子序列为{5,6,7,8},长度为4.
解法一:利用LCS法
可以把上面的问题转化为求最长公共子序列的问题。
(1) 排序A ----> 得到子序列 B。
(2) A和B求LCS即可。
解法二:naive迭代法 O(N^2)
时间复杂度:从前到后遍历每一个elem,每一elem都要与之前的所有i 做比较,这样时间复杂度为O(N^2)。
这是简单粗暴的方法。
解法三:动态规划法 O(NlogN)
假设存在一个序列d[1..9] = 2 1 5 3 6 4 8 9 7,可以看出来它的LIS长度为5。
下面一步一步试着找出它。
我们定义一个序列B,然后令 i = 1 to 9 逐个考察这个序列。
此外,我们用一个变量Len来记录现在最长算到多少了。
// 注意下面的“淘汰掉5”的过程
首先,把d[1]有序地放到B里,令B[1] = 2,就是说当只有len=1 一个数字2的时候,长度为1的LIS的最小末尾是2。这时Len=1
然后,把d[2]有序地放到B里,令B[1] = 1,就是说长度为1的LIS的最小末尾是1,d[1]=2已经没用了,很容易理解吧。这时Len=1
接着,d[3] = 5,d[3]>B[1],所以令B[1+1]=B[2]=d[3]=5,就是说长度为2的LIS的最小末尾是5,很容易理解吧。这时候B[1..2] = 1, 5,Len=2
再来,d[4] = 3,它正好加在1,5之间,放在1的位置显然不合适,因为1小于3,长度为1的LIS最小末尾应该是1,这样很容易推知,长度为2的LIS最小末尾是3,于是可以把5淘汰掉,这时候B[1..2] = 1, 3,Len = 2
继续,d[5] = 6,它在3后面,因为B[2] = 3, 而6在3后面,于是很容易可以推知B[3] = 6, 这时B[1..3] = 1, 3, 6,还是很容易理解吧? Len = 3 了噢。
第6个, d[6] = 4,你看它在3和6之间,于是我们就可以把6替换掉,得到B[3] = 4。B[1..3] = 1, 3, 4, Len继续等于3
第7个, d[7] = 8,它很大,比4大,嗯。于是B[4] = 8。Len变成4了
第8个, d[8] = 9,得到B[5] = 9,嗯。Len继续增大,到5了。
最后一个, d[9] = 7,它在B[3] = 4和B[4] = 8之间,所以我们知道,最新的B[4] =7,B[1..5] = 1, 3, 4, 7, 9,Len = 5。
于是我们知道了LIS的长度为5,且此时最后一个数字应该是 9。【有了这个线索,倒着遍历,发现9后,就可以过滤出想要的序列了】
注意。这个1,3,4,7,9不是LIS,它只是存储的对应长度LIS的最小末尾。有了这个末尾,我们就可以一个一个地插入数据。
虽然最后一个d[9] = 7更新进去对于这组数据没有什么意义,但是如果后面再出现两个数字 8 和 9,那么就可以把8更新到d[5], 9更新到d[6],得出LIS的长度为6。
然后应该发现一件事情了:在B中插入数据是有序的,而且是进行替换而不需要挪动——也就是说,我们可以使用二分查找,将每一个数字的插入时间优化到O(logN)~~~~~于是算法的时间复杂度就降低到了O(NlogN)
分解 “子问题”
硬币找零
如果我们有面值为1元、3元和5元的硬币若干枚,如何用最少的硬币凑够11元?
思维方式
首先我们思考一个问题,如何用最少的硬币凑够i元(i<11)?
1. 当我们遇到一个大问题时,总是习惯把问题的规模变小,这样便于分析讨论。
2. 这个规模变小后的问题和原来的问题是同质的,除了规模变小,其它的都是一样的, 本质上它还是同一个问题(规模变小后的问题其实是原问题的子问题)。
初始化
当i=0,即我们需要多少个硬币来凑够0元。 由于1,3,5都大于0,即没有比0小的币值,因此凑够0元我们最少需要0个硬币。
我们用 d(i)=j 来表示凑够i元最少需要j个硬币。
于是我们已经得到了 d(0)=0, 表示凑够0元最小需要0个硬币。
- 当i=1时,只有面值为1元的硬币可用, 因此我们拿起一个面值为1的硬币,接下来只需要凑够0元即可,而这个是已经知道答案的, 即 d(0)=0。
所以,d(1)=d(1-1)+1=d(0)+1=0+1=1。
- 当i=2时, 仍然只有面值为1的硬币可用,于是我拿起一个面值为1的硬币, 接下来我只需要再凑够2-1=1元即可(记得要用最小的硬币数量),而这个答案也已经知道了。
所以d(2)=d(2-1)+1=d(1)+1=1+1=2。
- 当i=3时,我们能用的硬币就有两种了:1元的和3元的。 既然能用的硬币有两种,我就有两种方案。
如果我拿了一个1元的硬币,我的剩下的目标就变为了: 凑够3-1=2元需要的最少硬币数量。即d(3)=d(3-1)+1=d(2)+1=2+1=3。
如果我拿了一个3元的硬币,我的剩下的目标就变为了: 凑够3-3=0元需要的最少硬币数量。即d(3)=d(3-3)+1=d(0)+1=0+1=1。
状态转移方程
这两种方案哪种更优呢? 记得我们可是要用最少的硬币数量来凑够3元的。
所以, 选择d(3)=1,怎么来的呢?具体是这样得到的:d(3) = min{d(3-1)+1, d(3-3)+1}。
可见,这边形成了一个三叉树(因为有三种情况1,3,5),而子问题就是当前问题的孩子,这些孩子已有了局部结果,直接用即可。
d(n) = min{ d(n-xi)+1 | i = types of coin}
巨量的子问题
理解:N(i,j) = N(i,j-i) + N(i-1, j)
以上只是求最优的一个解,即:最少的coin的方案。这其实是很多种组合中的一个。
那么,本来有多少种组合呢?(有点像“没有上级的宴会邀请问题”)
N(i, j)
- i:使用的面值最大的coin
- j:要构成的总价值
N(1, 1000) : 只有一种方案。
N(2, 1000) : 有好多种方案,很多很多,怎么算呢?
N(3, 1000) : 有更多种方案,很多很多,怎么算呢?
/* 一定使用i,即至少有一个i, 那么,剩下的价值最大的可能(bound)就是j-i。
* 不会使用i,会有多少种方案,这个子问题会提前被解。
*/
N(i,j) = N(i,j-i) + N(i-1, j)
|
N(i,j) = N(i,j-i) + N(i-1, j) |
|||||||
| N(3,1000) = N(3,997) + N(2, 1000) | |||||||
| N(3,997) | N(2, 1000) | ||||||
| N(3,994) | N(2, 997) | N(2,998) | N(1, 1000) | ||||
| N(3,991) | N(2,994) | N(2,995) | N(1,997) | N(2,996) | N(1,998) | ||
| N(3,988); N(2,991) | N(2,992); N(1,994) | N(2,993); N(1,995) | N(2,994); N(1,996) | ||||
| ... | ... | ... | ... | ||||
可见,最后结果是个极其庞大的数字。
感性理解
为何 N(2, 1000) = N(2, 998) + N(1, 1000) ?

假设1000不是全部由1构成,那么,出现在其中的2就肯定可以移动到顶端。
又因为这里是考虑的组合问题,而不是排列,所以,出现的2的这种情况就肯定能由x个左边的情况中的一种所表示。
其实就是:有2,或者没2;如果有2,那就等于1000减去这个2;
这个思维,与"叠海龟问题"中的”w+s最大的肯定能放在最下面“的思想是一致的。
再次理解 “子问题”
Devise a dynamic programming algorithm that counts the number of non-decreasing
sequences of integers of length N, such that the numbers are between 0 and M
inclusive.
举例:
#(3,2)表示:用数字1和2(条件是<=2)构成的len <=3的非递减序列有多少种?
| 1 | 2 | 1,1 | 1,2 | 2,2 | 1,1,1 | 1,1,2 | 1,2,2 | 2,2,2 |

#(5,10)= #(4,10)+ #(5,9)
考虑10时,
- 等号右侧左变量:有10,10已占坑,只需考虑剩下前四个即可#(4,10)。
- 等号右侧右变量:没10,最大只能是9,5个数字要从10前面的item里选择。
子问题变成了只能向右下角(终点)推进的二维数组模式。
进一步练习
背包问题
Integer Knapsack Problem (Duplicate Items NOT Allowed)
You have n items (some of which can be identical); item Ii is of weight wi and value vi.
You also have a knapsack of capacity C. Choose a combination of available itemswhich all fit in the knapsack and whose value is as large as possible.
Matrix 的横轴纵轴表示
子问题的表达:左黄 到 右黄 or 左黄 到 右下蓝


矩阵解释
数组f[i][j]:在只有i个物品,容量为j的情况下背包问题的最优解.
当物品种类变大为i+1时,最优解是什么?
第i+1个物品,假设:
-
- 能放进背包(前提是放得下),那么f[i+1][j]= f[i][j-weight[i+1]+value[i+1];
- 如果不放进背包,那么f[i+1][j]= f[i][j]。
这就得出了状态转移方程:
f[i+1][j]=max( f[i][j], f[i][j-weight[i+1]+value[i+1] )。
手动举例子
From: http://blog.csdn.net/mu399/article/details/7722810
条件:
-
- 有编号分别为a,b,c,d,e的五件物品,
- 它们的重量分别是2,2,6,5,4,
- 它们的价值分别是6,3,5,4,6,
- 现在给你个承重为10的背包,
如何让背包里装入的物品具有最大的价值总和?

现考虑 a4:
此时考虑a,但放不下了(此时的value=6是因为放了v(e) = 6)
接下来自然会想,是不是换一下袋子里的这个东东,能获得更大的value呢?此时,表格对子问题的记录就发挥作用了!
直接看sub-p:b2,看起来4-2->2有点 自动导航到所需子问题的味道。
结果是:你要分要放得下a,那么,能得到value为9这个方案。这个方案看起来更好呦。
所以,思维的关键就是要不要a的时候,看看两种不同情况下的value就好了。
Extended:
if Duplicate items allowed.
P = NP, 只能穷举。
Extended:
数字分组问题,将问题转化为求背包容量为所有数总和一半的背包问题。
生产线装配问题
问题描述
下图中可以看出按照红色箭头方向进行装配汽车最快,时间为38。分别现在装配线1上的装配站1、3和6,装配线2上装配站2、4和5。

寻找子问题
(1) 描述通过工厂最快线路的结构
对于装配线调度问题,一个问题的(找出通过装配站Si,j的 最快线路)最优解包含了子问题(找出通过S1,j-1或S2,j-1的最快线路)的一个最优解,这就是最优子结构。
观察一条通过装配站S1,j (在装配线1上) 的最快线路,会发现它必定是经过装配线1或2上装配站j-1。因此通过装配站的最快线路只能以下二者之一:
a) 通过装配线S1,j-1的最快线路,然后直接通过装配站Si,j;
b) 通过装配站S2,j-1的最快线路,从装配线2移动到装配线1,然后通过装配线S1,j。
为了解决这个问题,即寻找通过一条装配线上的装配站j的最快线路,需要解决其子问题,即寻找通过两条装配线上的装配站j-1的最快线路。
(子问题有两条路线罢了)
(2) 一个递归的解
最终目标是确定底盘通过工厂的所有路线的最快时间,设为f*,令fi[j]表示一个底盘从起点到装配站Si,j的最快时间,
则f* = min(f1[n]+x1, f2[n]+x2)。逐步向下推导,直到j=1。
-
- 当j=1时:
- f1[1] = e1+a1,1, f2[1] = e2+a2,1。
- 当j>1时:
- f1[j] = min(f1[j-1]+a1,j, f2[j-1]+t2,j-1+a1,j),
- f2[j] = min(f2[j-1]+a2,j, f1[j-1]+t1,j-1+a2,j)。
- 当j=1时:
Link: http://www.cnblogs.com/aabbcc/p/6509191.html
矩阵连乘
To evaluate (AB)C we need
(10 × 5) × 100 + (10 × 50) × 5 = 5000 + 2500 = 7500 multiplications;
To evaluate A(BC) we need
(100 × 50) × 5 + (10 × 50) × 100 = 25000 + 50000 = 75000 multiplications!如何使计算量最小?
Ref: https://cnbin.github.io/blog/2015/12/19/ju-zhen-lian-cheng-dong-tai-gui-hua-xiang-jie/
最优子结构
(1) 找出最优解的性质,刻画其特征结构
令 m[i][j] 表示第i个矩阵至第j个矩阵这段的最优解。从 i --> j
将矩阵连乘积 简记为A[i:j] ,这里i<=j。
假设这个最优解在第k处断开,i<=k<j,因为A[i:j]是最优的,那么A[i,k]和A[k+1:j]也是相应矩阵连乘的最优解。 // <-- 整体最优,内部分割也最优
可以用反证法证明之。 这就是最优子结构,也是用动态规划法解题的重要特征之一。
(2) 建立递归关系
设计算A[i:j],1≤i≤j≤n,所需要的最少数乘次数m[i,j],则原问题的最优值为m[1,n] 。
- 当i=j时,A[i,j]=Ai, m[i,j]=0;(表示只有一个矩阵,如A1,没有和其他矩阵相乘,故 乘的次数为0)
- 当i<j时,m[i,j] = min{ m[i,k] + m[k+1,j] + pi-1*pk*pj } , 其中 i<=k<j
相当于对i~j这段,把它分成2段,看哪种分法乘的次数最少,如:
A1,A2,A3,A4,则有3种分法:{A1}{A2A3A4}、{A1A2}{A3A4}、{A1A2A3}{A4},
其中,{}表示其内部是最优解,如{A1A2A3}表示是A1A2A3的最优解。

实践出真知
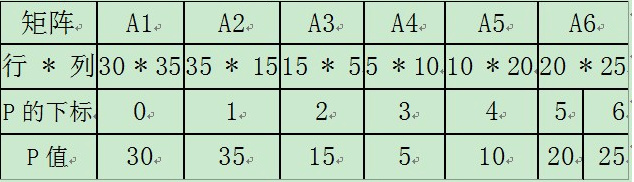
对于 p={30, 35, 15, 5, 10, 20, 25}:
计算顺序
每个对角线算是一组;总共有如下六组。
表中是可能的所有组合情况,需要计算选出每个表格中最小的一个组合方式。
“左下”的计算就将成为“右上”计算的 子问题集合!
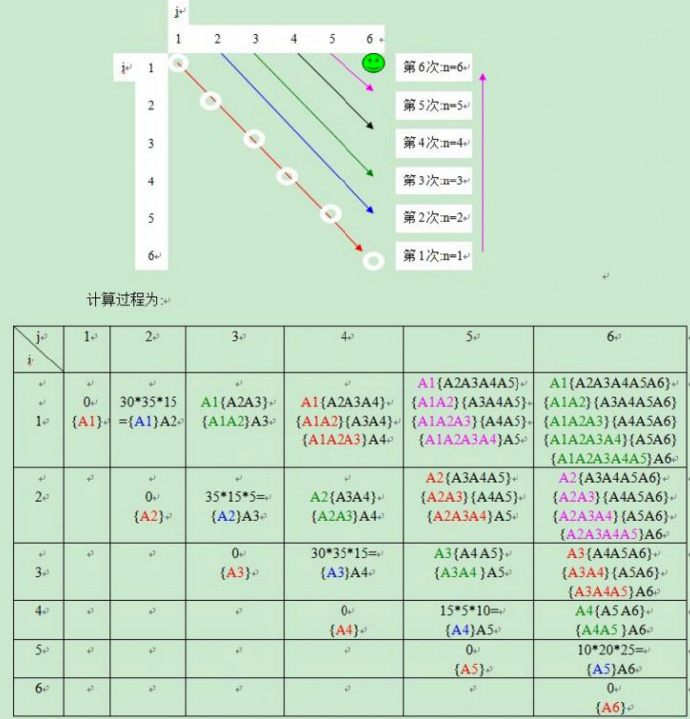
对上例,共6个矩阵(A1~A6),n=6,
当r=3时,r循环里面的是3个矩阵的最优解,i 从1->4,即 求的是 (r=3时 对角线是共四种情况)
(A1 A2 A3), (A2 A3 A4), (A3 A4 A5), (A4 A5 A6) 这4个矩阵段 (长度为3) 的最优解.
当i=2时,(A2 A3 A4) 的最优解为 { A2 (A3 A4) , (A2 A3) A4 } 的较小值。
思维技巧
花括号里的东西不用计算了,因为之前已经计算过了,只需要查表找到最优的方式,以及min value直接用即可。
Graph 的路径问题
Bellman-Ford算法
单源头最短路径,支持负权值
Dijkstra Algorithm
Dijkstra Algorithm Video: https://www.youtube.com/watch?v=RFEqcXSo_Zg
Dijkstra 算法采用贪心算法(Greedy Algorithm)范式进行设计,普通实现的时间复杂度为 O(V2),
若基于 Fibonacci heap 的最小优先队列实现版本则时间复杂度为 O(E + VlogV)。
Bellman-Ford Algorithm
Bellman-Ford Algorithm 和 Dijkstra 算法同为解决单源最短路径的算法。对于带权有向图 G = (V, E),
-
- Dijkstra 算法要求图 G 中边的权值均为非负。 // 基于贪心算法,普通实现的时间复杂度为 O(V2),若基于 Fibonacci heap 的最小优先队列实现版本则时间复杂度为 O(E + VlogV)
- Bellman-Ford 算法能适应一般的情况(即存在负权边的情况)。 // 基于动态规划,O(V*E)
一个实现的很好的 Dijkstra 算法比 Bellman-Ford 算法的运行时间要低。
Bellman-Ford 算法采用动态规划(Dynamic Programming)进行设计,实现的时间复杂度为 O(V*E),其中 V 为顶点数量,E 为边的数量。
Bellman-Ford 讲解
油管讲解: Bellman-Ford Algorithm Explained EASY
此链接讲得很明了。例如:
iteration: 3 D --> 7
// 建立在“子问题”之上,也就是上一个“列”。
S走三步到D,那么当然从上一次iter的两步的基础之上考虑!
- 上一轮中"非无限"的,有哪些直达D呢?(下图所示)
- C直达,且第二次iter时C=5,所以,5+2=7成为relax后的新值。
- F直达,且第二次iter时C=4,但是,4+3=7成为relax后的新值,以上面的新值一样。
- 再看下一个E。
可见这里体现了时间复杂度为O(V*E),就是矩阵的格子数。
【横轴:从S开始走几步能到达某个结点】

结果
最终的结果就是最后一列。
后一列比前一列更“优化”,值也就更“小”。
采用队列继续优化
Bellman-ford算法浪费了许多时间去做没有必要的松弛,
而 SPFA算法 用队列进行了优化,效果十分显著,高效难以想象。(后续再研究)
Floyd Warshall Algorithm
多源最短路径求法? 点击图片进入视频链接。
初始状态
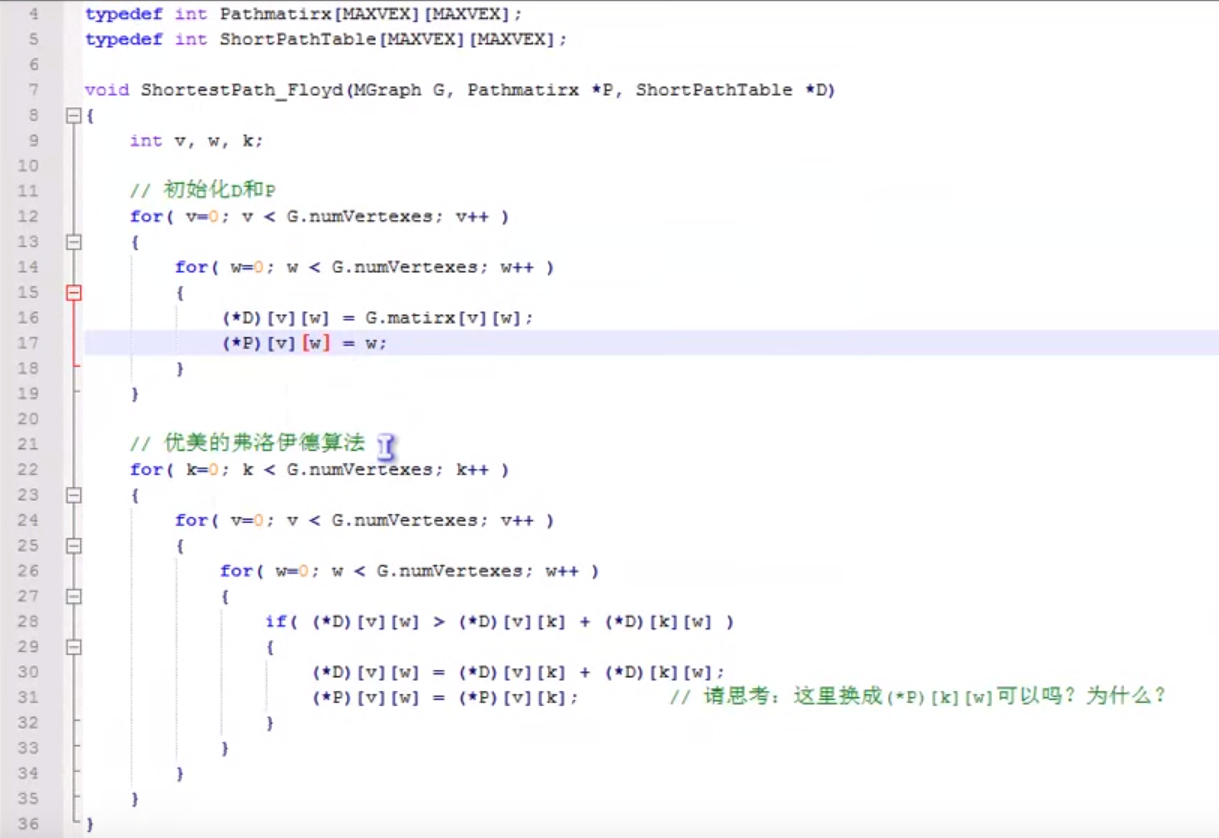
Ref: 65 小甲鱼数据结构与算法 最短路径(弗洛伊德算法)
P矩阵告诉我们:从v_x到v_y时必须要经过哪个点。


时间复杂度O(n^3)
最终状态

课后练习
Edit Distance
字符串变换的”最少操作“:
Given two text strings A of length n and B of length m, you
want to transform A into B. You are allowed to insert a character, delete a
character and to replace a character with another one. An insertion costs ci, a
deletion costs cd and a replacement costs cr.
Task: find the lowest total cost transformation of A into B
Ref: http://www.cnblogs.com/masterlibin/p/5785092.html
子问题:

Maximizing an expression
Instance: a sequence of numbers with operations +, −, × in between, for example
1 + 2 − 3 × 6 − 1 − 2 × 3 − 5 × 7 + 2 − 8 × 9
Task: Place brackets in a way that the resulting expression has the largest possible
value.Ref: https://courses.csail.mit.edu/6.006/fall10/psets/ps6/ps6-sol.pdf
答案:有点复杂,详见链接。
Extended:

逻辑表达式中插入符号,使结果为true。求有多少种方式。
上图为子问题:T(i, j) 的表达方式。
子问题看上去也得有O(n^2)个regression。
子字符串(隐含)出现的次数
We say that a sequence of Roman letters A occurs as a subsequence of a sequence
of Roman letters B if we can obtain A by deleting some of the symbols of B. Design
an algorithm which for every two sequences A and B gives the number of different
occurrences of A in B, i.e., the number of ways one can delete some of the symbols
of B to get A. For example, the sequence ba has three occurrences in the sequence
baba: baba, baba, baba.
Idea:
Based on Suffix matching.
The subproblem is to give the number of different occurences of substring of A in substring of B. (A的后缀字符串在B的后缀字符串出现的次数)
Algorithm:
-
-
In cell [row][col] write the value found at [row-1][col].
-
If sequence at row row and subsequence at column col start with the same char, add the value found at [row-1][col-1] to the value just written to [row][col].
-
求最大子数组的和 in O(n)
给定一个数组,它里面全是一些数字,要找出不论什么连续的值中最大的和. 例: 已有数组:{31, -41, 59, 26, -53, 58, 97, -93, -23, 84}
它的连续的值最大的和则是第 2 个值到第 6 个值的合:187.
如果用函数f(i)表示以第i个数字结尾的子数组的最大和,那么我们需要求出max(f[0...n])。我们可以给出如下递归公式求f(i)

这个公式的意义:
- 当以第(i-1)个数字为结尾的子数组中所有数字的和f(i-1)小于0时,如果把这个负数和第i个数相加,得到的结果反而不第i个数本身还要小,所以这种情况下最大子数组和是第i个数本身。
- 如果以第(i-1)个数字为结尾的子数组中所有数字的和f(i-1)大于0,与第i个数累加就得到了以第i个数结尾的子数组中所有数字的和。
| 31 | -41 | 59 | 26 | -53 | 58 | 97 | -93 | -23 | 84 | |
| -10 | 85 | 32 | 90 | 187 | 94 | 71 | 155 | |||
| 31 | -10 | 59 | 85 | 32 | 90 | 187 | 94 | 71 | 155 |
动态规划,众所周知,第一步就是找子问题,也就是把一个大的问题分解成子问题。这里我们设两个字符串A、B,A = "a0, a1, a2, ..., am-1",B = "b0, b1, b2, ..., bn-1"。
-
不相邻的子数组
Ref: Maximum sum such that no two elements are adjacent | GeeksforGeeks
上题的扩展:构成子数组的元素需“不相邻”,又当如何呢?
基本思路:
1. Loop for all elements in arr[].
2. Maintain two sums incl and excl
3
incl =Max sum including the previous element.
excl = Max sum excluding the previous element.
4. step by step
arr[] = {5, 5, 10, 40, 50, 35}

初始化:incl = 5; excl = 0
| (1) | incl | 0 + 5 | 5 | |
| 5 | excl | max(5, 0) | 5 | |
| (2) | incl | 5 + 10 | 15 | 包含当前的10的话,最大值会是多少 |
| 10 | excl | max(5, 5) | 5 | 不包含当前10的话, |
| (3) | incl | 5 + 40 | 45 | 包含40,就直接考虑“不包含previous”的10的结果即可。 |
| 40 | excl | max(15, 5) | 15 | |
| (4) | incl | 15 + 50 | 65 | |
| 50 | excl | max(45, 15) | 45 | |
| (5) | incl | 45 + 35 | 80 | <---- final answer |
| 35 | excl | max(65, 45) | 65 |
Ref: Maximum sum such that no two elements are adjacent | GeeksforGeeks
int FindMaxSum(int arr[], int n) { int inc1 = arr[0]; int excl = 0; int excl_new; int i; for (i = 1; i < n; i++) { excl_new = ( inc1 >excl ) ? inc1 : exc1;
incl = excl + arr[i]; excl = excl_new; } return ( (incl > excl) ? incl :excl ); }
End.






