[CNN] What is Convolutional Neural Network

参数手动计算练习

---

Ref: 从LeNet-5看卷积神经网络CNNs

关于这篇论文的一些博文的QAC:

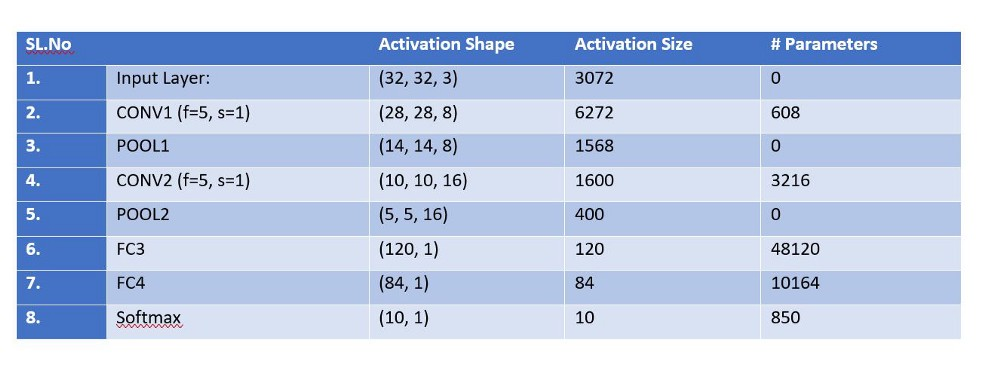
参数计算

一、基本原理

MLP（Multilayer Perceptron，多层感知器）是一种前向神经网络（如下图所示），相邻两层网络之间全连接。 

sigmoid通常使用tanh函数和logistic函数。

• 模型结构

1998年Yann LeCun在论文“Gradient-Based Learning Applied to Document Recognition”中提出了LeNet-5，并在字母识别中取得了很好的效果。LeNet-5的结构如下图所示：

  

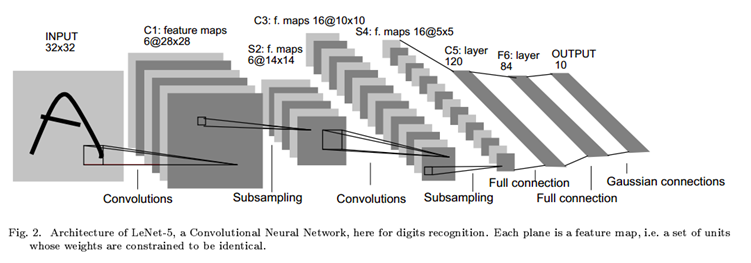
• 计算方法

  • input：输入图片，32*32像素；
  • C1：5*5卷积核，生成6个feature maps，共需要（6*5*5 + 6）=156个参数；（卷积核就代表参数）
  • S2：2*2个像素相加，然后乘以一个参数，加上一个偏置，共计2*6=12个参数；
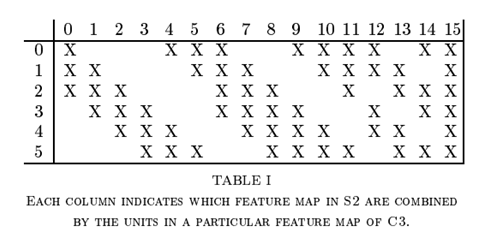
  • C3：5*5卷积核，生成16个feature maps，每个feature map由S2中若干个feature maps卷积得到，如图Table1所示；
  • S4：和S2相同的操作，共计16*2 = 32个参数；
  • C5：与S4全连接，共计（5*5*16*120+120）=48120个参数；
  • F6：与C5全连接，共计（120*84+84） = 10164 个参数；
  • output: 与F6全连接。

 

Pooling 也可以不考虑 “占用” parameters。

 

 

 

 

 

 

 

 

 

 

 

二、卷积 convolution

        C1/C3/C5这三层都用了卷积操作，学过数字图像处理的同学一定对这种图像上的卷积很熟悉，本质上是用一块权重模板在图像上的各个区域做加权求和，如下图所示：

 

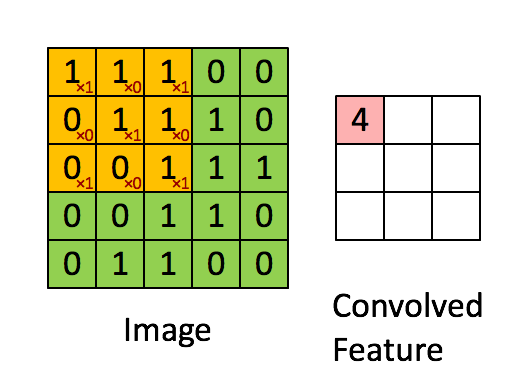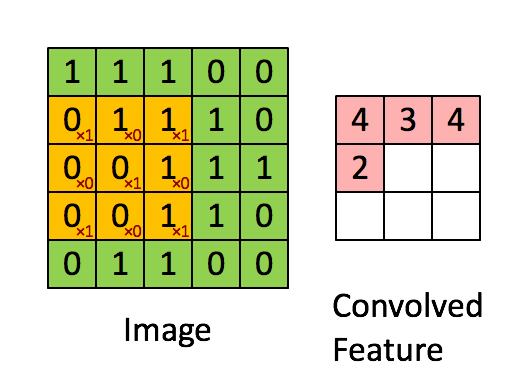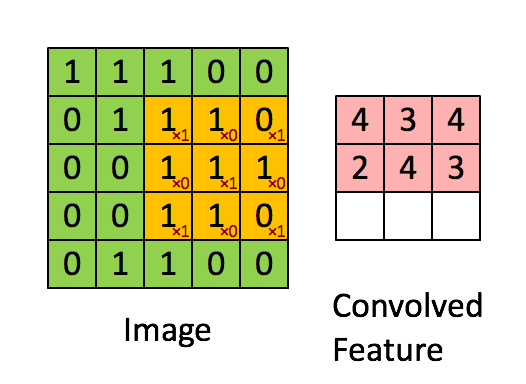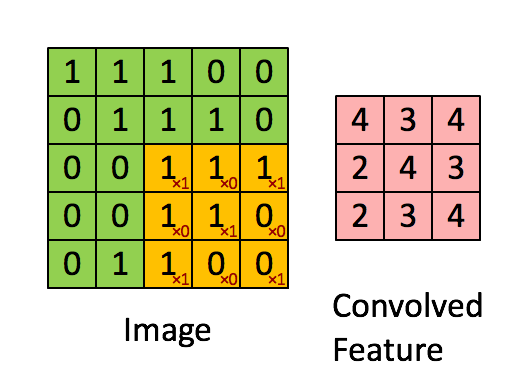
图中黄色的3*3 卷积核从图像的左上角开始向右或向下移动，对移动过程中覆盖的区域求加权和。最后得到(5-3+1)*(5-3+1)大小的卷积结果，称为一个feature map。

C1: LeNet-5的C1层用6个 5*5卷积核对输入的32*32图像进行卷积，每个卷积核对应生成一个(32-5+1)*(32-5+1)的feature map，共计6个feature map。

C3: C3的过程稍为复杂，C3总共生成了16个feature map，每个feature map按照Table1选择输入。例如C3编号为0的feature map是由S2中编号为0、1、2的feature map 生成的。先由3个卷积核分别在S2的0、1、2 feature map上生成3个临时feature map，然后把这三个临时feature map相加得到C3的feature map 0。这样构造C3 有两个好处：一是相比于全连接，可以减少参数的数量；二是每个feature map的输入都不相同，可以达到互补的效果。

C5: C5层用全连接的方式，每个feature map都是由S4中所有的feature map卷积结果求和得到的。由于S4的feature map大小是5*5，卷积核大小也是5*5，所以卷积后得到的是一个1*1的矩阵。

另外，C1/C3/C5每个feature map计算结果都会在计算结尾加上一个偏置。

 

三、池化 pooling

池化的作用主要有两个：一是减少参数数量；二是在使模型具有较好的平移不变性。

和卷积很类似，不同之处在于卷积核覆盖的区域是重叠的，而池化的各个区域是没有重叠的。所以当S2/S4用2*2的池化模板后，feature map的宽和高都减小为原来的一半。

再借用一下UFLDL Tutorial关于池化的示意图： 

.

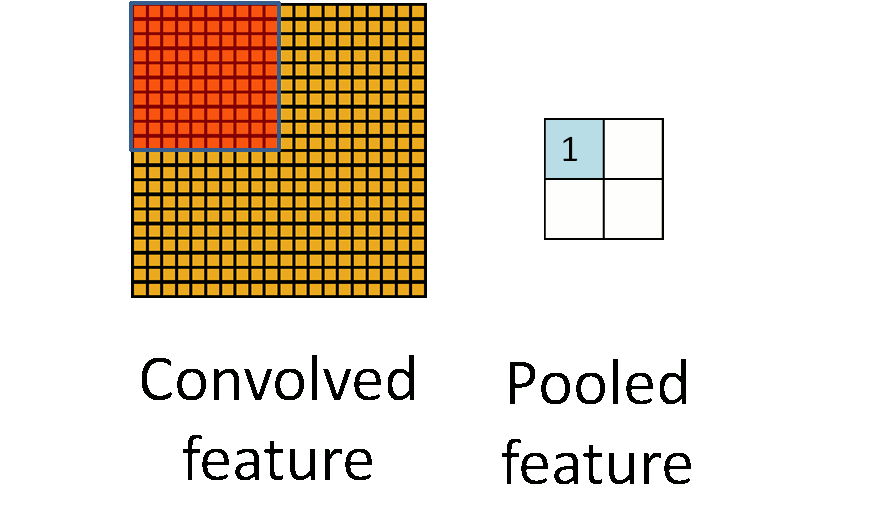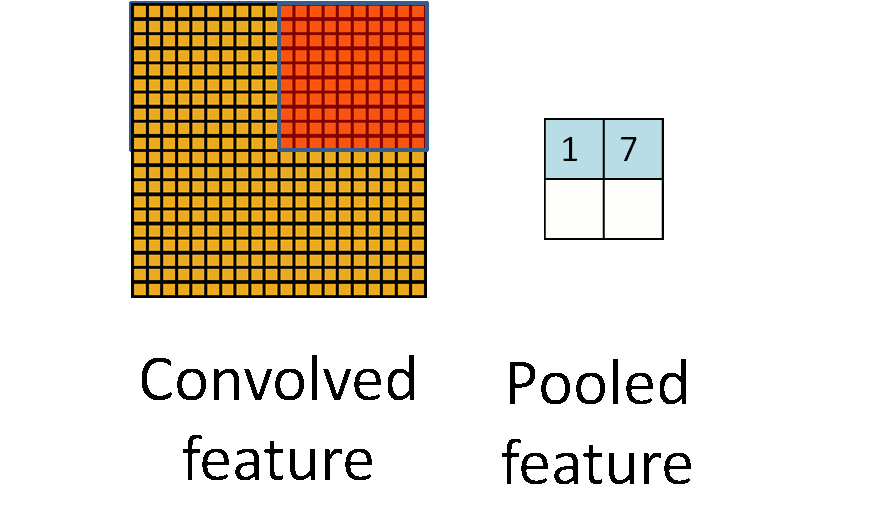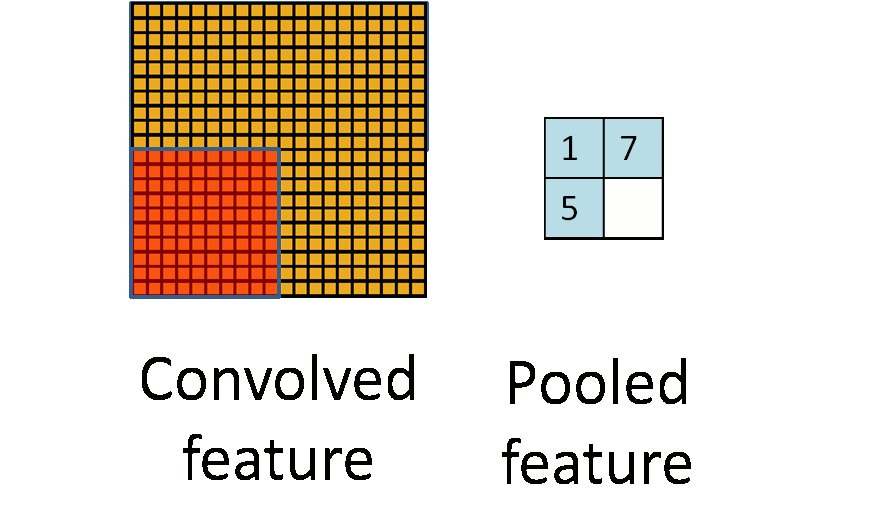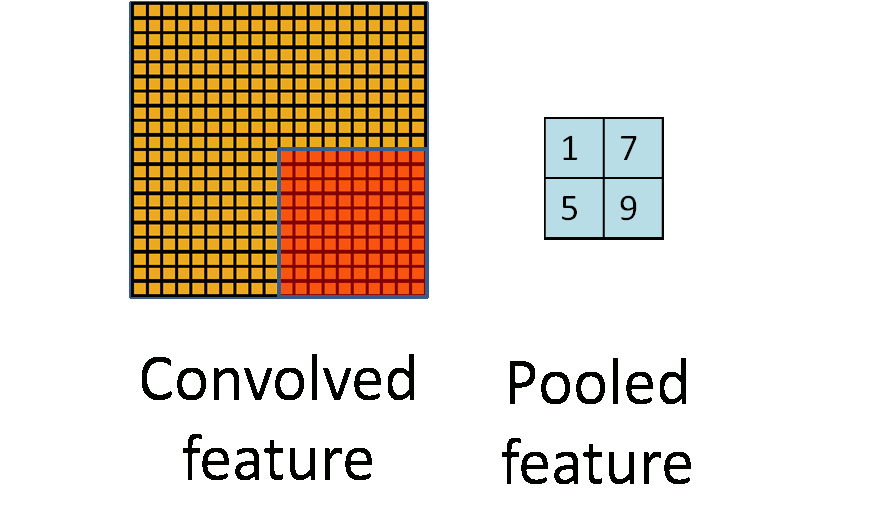
四、输出层 output

output层/F6层都是与前一层全连接，C5-F6-output整体结构可以看成一个多层感知器。

所以LeNet-5其实是由三种不同的结构组成的：卷积、池化、多层感知器。而使用这三种结构也就可以构成大部分卷积神经网络了。

 

 

边边角角问题

(1) 卷积核是学习得来，还是预定义好的？

整个网络的训练，主要就是为了学那个卷积核啊。

 

(2) 有哪些参数？

如果是卷积层输出4个feature map，那么它就有4个卷积核。
自定义的其实有卷积核的kernel_size，也就是kernel_width和kernel_height，

然后num_output就是输出的feature map个数。

还有一个数字其实也跟卷积核有关，这个卷积层的输入的channel数量.

总的来说，决定卷积层里面卷积核的参数数量的数字总共有4个：num_output, num_channel, kernel_height, kernel_width。

(3) channel是什么？

对一张RGB图像经过一个卷积核得到的是一张feature map。

原理是这样的，通常所说的2D卷积其实是3D的（卷积核的维度应该是kernel_height * kernel_height * input_channel），只不过第三个维度恰好等于输入通道的个数，所以卷了以后在第三个维度上就没了，变成了扁平的二维feature map，所以叫2D卷积。

另一种理解方式是，一个卷积核的形状是 kernel_height * kernel_height，并且有input_channel层，把它和输入图像做卷积的过程是这样的：

用卷积核的第一层 和 输入图像的第一个通道 做一次2D卷积，

用卷积核的第二层 和 输入图像的第二个通道 做一次2D卷积，

……，

用卷积核的最后一层和输入图像的最后一个通道做一次2D卷积，

于是得到了input_channel 个 feature map，最后把这input_channel 个 feature map 对应位置加起来，最后得到一张feature map，这就是卷积的结果。

 

 

认识卷积

• 卷积层的参数共享

 

 

卷积核的参数就是神经网络的输入层。

Next: [CNN] Understanding Convolution

 

• 补充：第九章 - 卷积网络

卷积运算通过三个重要的思想来帮助改进机器学习系统：

• • 稀疏交互（sparse interactions）、
  • 参数共享（parameter sharing）、
  • 等变表示（equivariant representations）。

 

最大池化

引入了不变性。

无限强的先验：

方差越大，信息越大；

在决定参数最终取值时起着更加积极的作用。

 

也就是限制比较多，例如权重共享这样的例子，相邻关系一定强等等。

 

卷积边缘填充方式

零填充（有效卷积）：m-k+1

必要零填充（相同卷积）

全填充：m+k-1

 

End.