[Algorithm] Beating the Binary Search algorithm – Interpolation Search, Galloping Search

本篇补充了Python版本的实现 Sep 2019.

---

顺序查找

如果是 ”随机放置“，则使用。

# Python

def sequentialSearch(alist, item):
　　pos = 0
　　found = False

　　while pos < len(alist) and not Found: 
　　　　if alist[pos] == item:
　　　　　　found = True
　　　　else: 
　　　　　　pos = pos + 1

　　return found

 

 

二分检索

代码可写成：递归，也可以是非递归。

# Python

def binarySearch(alist, item):
    if len(alist) == 0:
        return False
    else:
        midpoint = len(alist)//2
        if alist[midpoint] == item:
            return True
        else:
            # 不断调整 "中间值" 即可
            if item<alist[midpoint]:
                return binarySearch(alist[:midpoint], item)
            else:
                return binarySearch(alist[midpoint+1:], item)

testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binarySearch(testlist, 3))
print(binarySearch(testlist, 13))




def binarySearch2(alist, item):
    first = 0
    last = len(alist)-1
    found = False

    while first < last and not found:
        midpoint = (first + last) // 2 
        if alist[midpoint] == item:
            found = True
        else:
            # 不断调整 "中间值" 即可
            if item < alist[midpoint]:
                last = midpoint - 1
            else:
                first = midpoint + 1

    return found

testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binarySearch2(testlist, 3))
print(binarySearch2(testlist, 13))

 

渴望对手

From: http://blog.jobbole.com/73517/

二分检索是查找有序数组最简单然而最有效的算法之一。现在的问题是，更复杂的算法能不能做的更好？

有些情况下，散列整个数据集是不可行的，或者要求既查找位置，又查找数据本身。这个时候，用哈希表就不能实现O(1)的运行时间了。但对有序数组， 采用分治法通常可以实现O(log(n))的最坏运行时间。

在下结论前，有一点值得注意，那就是可以从很多方面“击败”一个算法：所需的空间，所需的运行时间，对底层数据结构的访问需求。接下来我们做一个运行时对比实验，实验中创建多个不同的随机数组，其元素个数均在10,000到81,920,000之间，元素均为4字节整型数据。

 

非缓存友好

二分检索算法的每一步，搜索空间总会减半，因此保证了运行时间。在数组中查找一个特定元素，可以保证在 O(log(n))时间内完成，而且如果找的正好是中间元素就更快了。也就是说，要从81,920,000个元素的数组中找某个元素的位置，只需要27个甚至更少的迭代。

由于二分检索的随机跳跃性，该算法并非缓存友好的，因此只要搜索空间小于特定值（64或者更少），一些微调的二分检索算法就会切换回线性检索继续查找。然而，这个最终的空间值是极其架构相关的，因此大部分框架都没有做这个优化。

 

 

快速检索

也叫作 "飞驰检索": http://www.cnblogs.com/jesse123/p/6026029.html

第一步

如果由于某些原因，数组长度未知，快速检索可以识别初始的搜索域。这个算法从第一个元素开始，一直加倍搜索域的上界，直到这个上界已经大于待查关键字。

 

第二步

之后，根据实现不同，

• • 或者采用标准的二分检索查找，保证O(log(n)) 的运行时间
  • 或者开始另一轮的快速检索。更接近O(n)的运行时间。

如果我们要找的元素比较接近数组的开头，快速检索就非常有效。 

 

 

抽样检索

抽样检索有点类似二分检索，不过在确定主要搜索区域之前，它会先从数组中拿几个样例。最后，如果范围足够小，就采用标准的二分检索确定待查元素的准确位置。这个理论很有趣，不过在实践中执行效果并不好。

 

 

插值检索

优化一，按照比例找下一个分界点

对于插值查找，就是对于二分查找的优化，将二分查找中的 mid = (low + high) / 2 ----> 改为 ----> mid = low + (high - low) * (key - a[low]) / (a[high] - a[low])。

插值查找是根据查找关键子key与查找表中最大最小记录关键字比较后的查找方法，核心在于插值计算公式(key-a[low])/(a[high] - a[low])。

 

 

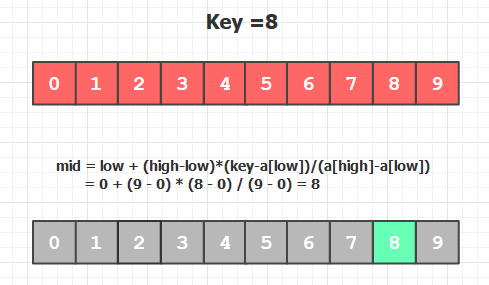
最后也可以回归到顺序查找的插值检索。

在被测的算法中，插值检索可以说是“最聪明”的一个算法。它类似于人类使用电话簿的方法，它试图通过假设元素在数组中均匀分布，来猜测元素的位置。

首先，它抽样选择出搜索空间的开头和结尾，然后猜测元素的位置。算法一直重复这个步骤，直到找到元素。

• • 如果猜测是准确的，比较的次数大概是O(log(log(n))，运行时间大概是O(log(n))；
  • 但如果猜测的不对，运行时间就会是O(n)了。

 

优化二，Interpolation + Seq

插值检索的一个改进版本是，只要可推测我们猜测的元素位置是接近最终位置的，就开始执行顺序查找。

相比二分检索，插值检索的每次迭代计算代价都很高，因此在最后一步采用顺序查找，无需猜测元素位置的复杂计算，很容易就可以从很小的区域（大概10个元素）中找到最终的元素位置。

围绕插值检索的一大疑问就是，O(log(log(n))的比较次数可能产生O(log(log(n))的运行时间。这并非个案，因为存储访问时间和计算下一次猜测的CPU时间相比，这两者之间要有所权衡。

 

大数据查找优势

如果数据量很大，而且存储访问时间也很显著，比如在一个实际的硬盘上，插值检索轻松击败二分检索。然而，实验表明，如果访问时间很短，比如说RAM，插值检索可能不会产生任何好处。

 

　　 

 

试验结果

---

每次检索的统计

试验中的源代码都是用Java写的；每个实验在相同的数组上运行10次；数组是随机产生的整型数组，存储在内存中。

在插值检索中，首先会采用抽样检索，从检索空间拿20个样例，以确定接下来的搜索域。如果假定的域只有10个或更少的元素，就开始采用线性检索。另外，如果这个搜索域元素个数小于2000，就回退到标准的二分检索了。

作为参考，java默认的Arrays.binarySearch算法也被加入实验，以同自定义的算法对比运行时间。

 

尽管我们对插值检索期望很高，它的实际运行时间并未击败java默认的二分检索算法。如果存储访问时间长，结合采用某些类型的哈希树和B+树可能是一个更好的选择。

但值得注意的是，对均匀分布的数组，组合使用插值检索和顺序检索在比较次数上总能胜过二分检索。不过平台的二分检索已经很高效，所以很多情况下，可能不需要用更复杂的算法来代替它。

 

平均运行时间 / 每次检索

Size	Arrays. binarySearch	Interpolation +Seq	Interpolation	Sampling	Binary	Gallop	Gallop +Binary
10,000	1.50E-04 ms	1.60E-04 ms	2.50E-04 ms	3.20E-04 ms	5.00E-05 ms	1.50E-04 ms	1.00E-04 ms
20,000	5.00E-05 ms	5.50E-05 ms	1.05E-04 ms	2.35E-04 ms	7.00E-05 ms	1.15E-04 ms	6.50E-05 ms
40,000	4.75E-05 ms	5.00E-05 ms	9.00E-05 ms	1.30E-04 ms	5.25E-05 ms	1.33E-04 ms	8.75E-05 ms
80,000	4.88E-05 ms	5.88E-05 ms	9.88E-05 ms	1.95E-04 ms	6.38E-05 ms	1.53E-04 ms	9.00E-05 ms
160,000	5.25E-05 ms	5.94E-05 ms	1.01E-04 ms	2.53E-04 ms	6.56E-05 ms	1.81E-04 ms	9.38E-05 ms
320,000	5.16E-05 ms	6.13E-05 ms	1.22E-04 ms	2.19E-04 ms	6.31E-05 ms	2.45E-04 ms	1.04E-04 ms
640,000	5.30E-05 ms	6.06E-05 ms	9.61E-05 ms	2.12E-04 ms	7.27E-05 ms	2.31E-04 ms	1.16E-04 ms
1,280,000	5.39E-05 ms	6.06E-05 ms	9.72E-05 ms	2.59E-04 ms	7.52E-05 ms	2.72E-04 ms	1.18E-04 ms
2,560,000	5.53E-05 ms	6.40E-05 ms	1.11E-04 ms	2.57E-04 ms	7.37E-05 ms	2.75E-04 ms	1.05E-04 ms
5,120,000	5.53E-05 ms	6.30E-05 ms	1.26E-04 ms	2.69E-04 ms	7.66E-05 ms	3.32E-04 ms	1.18E-04 ms
10,240,000	5.66E-05 ms	6.59E-05 ms	1.22E-04 ms	2.92E-04 ms	8.07E-05 ms	4.27E-04 ms	1.42E-04 ms
20,480,000	5.95E-05 ms	6.54E-05 ms	1.18E-04 ms	3.50E-04 ms	8.31E-05 ms	4.88E-04 ms	1.49E-04 ms
40,960,000	5.87E-05 ms	6.58E-05 ms	1.15E-04 ms	3.76E-04 ms	8.59E-05 ms	5.72E-04 ms	1.75E-04 ms
81,920,000	6.75E-05 ms	6.83E-05 ms	1.04E-04 ms	3.86E-04 ms	8.66E-05 ms	6.89E-04 ms	2.15E-04 ms

 

平均比较次数 / 每次检索

Size	Arrays. binarySearch	Interpolation +Seq	Interpolation	Sampling	Binary	Gallop	Gallop +Binary
10,000	?	10.6	17.6	19.0	12.2	58.2	13.2
20,000	?	11.3	20.7	19.0	13.2	66.3	14.2
40,000	?	11.0	16.9	20.9	14.2	74.9	15.2
80,000	?	12.1	19.9	38.0	15.2	84.0	16.2
160,000	?	11.7	18.3	38.0	16.2	93.6	17.2
320,000	?	12.4	25.3	38.2	17.2	103.8	18.2
640,000	?	12.4	19.0	41.6	18.2	114.4	19.2
1,280,000	?	12.5	20.2	57.0	19.2	125.5	20.2
2,560,000	?	12.8	22.7	57.0	20.2	137.1	21.2
5,120,000	?	12.7	26.5	57.5	21.2	149.2	22.2
10,240,000	?	13.2	25.2	62.1	22.2	161.8	23.2
20,480,000	?	13.4	23.4	76.0	23.2	175.0	24.2
40,960,000	?	13.4	21.9	76.1	24.2	188.6	25.2
81,920,000	?	14.0	19.7	77.0	25.2	202.7	26.2

 

源代码 点此获取检索算法的完整源代码。注意，代码不是产品级别的；比如，在某些例子里，可能有过多或过少的范围检查。