[OpenCV] Feature Extraction

特征检测

特征描述

特征匹配

特征跟踪

 

---

 

“不读白不读，读了还想读” 的一本基础书

---

 

低层次特征提取

阈值方法

1. 边缘检测

　　一阶检测算子

　　二阶检测算子

　　相位一致性（频域）

2. 角点检测（局部特征提取）

3. 光流（optical flow）

 

一阶边缘检测算子

基础算子：Roberts交叉算子

Prewitt算子

Sobel算子

Canny算子 (most popular recently)

既然号称“最优算子”，那就作为典型，深入一下。

Canny 的目标是找到一个最优的边缘检测算法，最优边缘检测的含义是：
(1)最优检测：
　　算法能够尽可能多地标识出图像中的实际边缘，漏检真实边缘的概率和误检非边缘的概率都尽可能小；
(2)最优定位准则：
　　检测到的边缘点的位置距离实际边缘点的位置最近，或者是由于噪声影响引起检测出的边缘偏离物体的真实边缘的程度最小；
(3)检测点与边缘点一一对应：
　　算子检测的边缘点与实际边缘点应该是一一对应。

为了满足这些要求 Canny 使用了变分法（calculus of variations），这是一种寻找优化特定功能的函数的方法。最优检测使用四个指数函数项表示，但是它非常近似于高斯函数的一阶导数。


近似的实现：
1.高斯平滑处理
2.sobel处理
3.非极大值抑制（即最后会保留一条边界处最亮的一条细线）
4.连接边缘点的滞后阈值处理 （和强边界相连的弱边界认为是边界，其他的弱边界则被抑制）


双阈值（Double Thresholding） 
经过非极大抑制后图像中仍然有很多噪声点。Canny算法中应用了一种叫双阈值的技术。
即设定一个阈值上界和阈值下界（opencv中通常由人为指定的），
　　图像中的像素点如果大于阈值上界则认为必然是边界（称为强边界，strong edge），
　　小于阈值下界则认为必然不是边界，
　　两者之间的则认为是候选项（称为弱边界，weak edge），需进行进一步处理。

 

二阶边缘检测算子

基础算子：Laplacian算子

不能得到边缘方向，但计算成本低。

与高斯平滑结合后得到的Laplacian of Gaussian算子

Marr-Hildreth算子

http://blog.csdn.net/tonyshengtan/article/details/43794359 

 

 

• 性质1，该模板对平坦区域应该无响应，所以算子内系数和应该为0，使用公式计算出来的结果不为零，需要整体上下平移模板
• 性质2，LoG可以使用laplace算子和高斯模板进行卷积后求得，其等效于使用LoG大小和标准差的高斯平滑后得到laplace结果
• 性质3，得到的结果要检测零交叉来定位边缘，因为噪声等原因，这里进行判断时可以使用阈值，也就是当出现零交叉的时候还要判断下正负值的差的绝对值是否满足阈值要求。
• 性质4，LoG模板的大小和标准差的选择关系，遵循高斯分布的3δ原则，也就是当位置超过均值正负3δ以外的值很小，也就是说，LoG模板应该选择大于6δ的最小奇数作为模板大小，过大效果不会有提高反而增加计算量，过小会造成截断，无法得到正确结果。

Spacek算子

Petrou算子

补充：performance 需要被量化，比如利用统计测试来评价边缘检测算子的性能（Yitzhaky and peli, 2003）。

 

相位一致性 

1. 可以检测大范围的特征。

2. 对局部光照变化具有不变性。

 

---

 

 

基于曲率的角点算子

- 边缘方向的差值。

- 亮度变化计算曲率

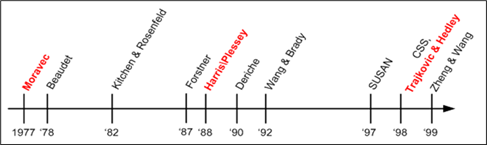
- 考虑图像P在特点方向上的变化来计算曲率(Moravec --> Harris检测器)

- FAST(SUSAN)角点检测

- 现代方法：区域/图像块分析

 

 

Harris详解 from 同道中人

1. 不同类型的角点

从图像分析的角度来定义角点可以有以下两种定义：

1. 1. 角点可以是两个边缘的角点；
   2. 角点是邻域内具有两个主方向的特征点；

前者往往需要对图像边缘进行编码，这在很大程度上依赖于图像的分割与边缘提取，具有相当大的难度和计算量，且一旦待检测目标局部发生变化，很可能导致操作的失败。早期主要有Rosenfeld和Freeman等人的方法，后期有CSS等方法。

基于图像灰度的方法通过计算点的曲率及梯度来检测角点，避免了第一类方法存在的缺陷，此类方法主要有Moravec算子、Forstner算子、Harris算子、SUSAN算子等。

这篇文章主要介绍的Harris角点检测的算法原理，比较著名的角点检测方法还有jianbo Shi和Carlo Tomasi提出的Shi-Tomasi算法，这个算法开始主要是为了解决跟踪问题，用来衡量两幅图像的相似度，我们也可以把它看为Harris算法的改进。

OpenCV中已经对它进行了实现，接口函数名为GoodFeaturesToTrack()。

另外还有一个著名的角点检测算子即SUSAN算子，SUSAN是Smallest Univalue Segment Assimilating Nucleus（最小核值相似区）的缩写。

SUSAN使用一个圆形模板和一个圆的中心点，通过圆中心点像素与模板圆内其他像素值的比较，统计出与圆中心像素近似的像元数量，

当这样的像元数量小于某一个阈值时，就被认为是要检测的角点。

我觉得可以把SUSAN算子看为Harris算法的一个简化。这个算法原理非常简单，算法效率也高，所以在OpenCV中，它的接口函数名称为：FAST() 。

 

2. Harris角点

2.1 基本原理

人眼对角点的识别通常是在一个局部的小区域或小窗口完成的。如果在各个方向上移动这个特征的小窗口，窗口内区域的灰度发生了较大的变化，那么就认为在窗口内遇到了角点。

如果这个特定的窗口在图像各个方向上移动时，窗口内图像的灰度没有发生变化，那么窗口内就不存在角点；

如果窗口在某一个方向移动时，窗口内图像的灰度发生了较大的变化，而在另一些方向上没有发生变化，那么，窗口内的图像可能就是一条直线的线段(边缘)。

 

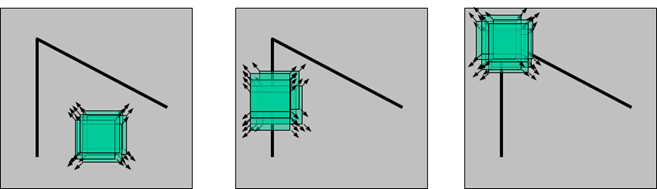
2.3 Harris角点的性质

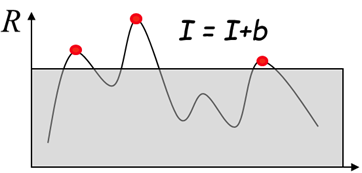
1. 参数α对角点检测的影响

由此，可以得出这样的结论：

增大α值，将减小角点响应值R，降低角点检测的灵敏性，减少被检测角点的数量；

减小α值，将增大角点响应值R，增加角点检测的灵敏性，增加被检测角点的数量。

2. Harris角点检测算子对亮度和对比度的变化不敏感

这是因为在进行Harris角点检测时，使用了微分算子对图像进行微分运算，而微分运算对图像密度的拉升或收缩和对亮度的抬高或下降不敏感。

换言之，对亮度和对比度的仿射变换并不改变Harris响应的极值点出现的位置，但是，由于阈值的选择，可能会影响角点检测的数量。

 

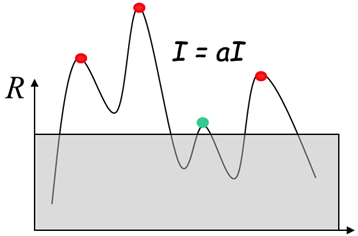
3. Harris角点检测算子具有旋转不变性

Harris角点检测算子使用的是角点附近的区域灰度二阶矩矩阵。

而二阶矩矩阵可以表示成一个椭圆，椭圆的长短轴正是二阶矩矩阵特征值平方根的倒数。

当特征椭圆转动时，特征值并不发生变化，

所以判断角点响应值R也不发生变化，由此说明Harris角点检测算子具有旋转不变性。

 

4. Harris角点检测算子不具有尺度不变性

如下图所示，当右图被缩小时，在检测窗口尺寸不变的前提下，在窗口内所包含图像的内容是完全不同的。左侧的图像可能被检测为边缘或曲线，而右侧的图像则可能被检测为一个角点。

 

2.4 Harris的OpenCV接口

OpenCV的Hairrs角点检测的函数为cornerHairrs()，但是它的输出是一幅浮点值图像，浮点值越高，表明越可能是特征角点，我们需要对图像进行阈值化。

C++: void cornerHarris(InputArray src, OutputArray dst, int blockSize, int apertureSize, double k, int borderType = BORDER_DEFAULT);

• • src – 输入的单通道8-bit或浮点图像。
  • dst – 存储着Harris角点响应的图像矩阵，大小与输入图像大小相同，是一个浮点型矩阵。
  • blockSize – 邻域大小。
  • apertureSize – 扩展的微分算子大。
  • k – 响应公式中的，参数α。
  • boderType – 边界处理的类型。

int main()
{
    Mat image = imread("../buliding.png");
    Mat gray;
    cvtColor(image, gray, CV_BGR2GRAY);

    Mat cornerStrength;
    cornerHarris(gray, cornerStrength, 3, 3, 0.01);
    threshold(cornerStrength, cornerStrength, 0.001, 255, THRESH_BINARY);
    return 0;
}

 

          

从上面上间一幅图像我们可以看到，有很多角点都是粘连在一起的，我们下面通过加入非极大值抑制来进一步去除一些粘在一起的角点。

非极大值抑制原理是，在一个窗口内，如果有多个角点则用值最大的那个角点，其他的角点都删除，窗口大小这里我们用3*3，程序中通过图像的膨胀运算来达到检测极大值的目的，因为默认参数的膨胀运算就是用窗口内的最大值替代当前的灰度值。

int main()
{
    Mat image = imread("buliding.png");
    Mat gray;
    cvtColor(image, gray, CV_BGR2GRAY);

    Mat cornerStrength;
    cornerHarris(gray, cornerStrength, 3, 3, 0.01);

    double maxStrength;
    double minStrength;
    // 找到图像中的最大、最小值
    minMaxLoc(cornerStrength, &minStrength, &maxStrength);

    Mat dilated;
    Mat locaMax;
    // 膨胀图像，最找出图像中全部的局部最大值点
    dilate(cornerStrength, dilated, Mat());
    // compare是一个逻辑比较函数，返回两幅图像中对应点相同的二值图像
    compare(cornerStrength, dilated, locaMax, CMP_EQ);

    Mat cornerMap;
    double qualityLevel = 0.01;
    double th = qualityLevel*maxStrength; // 阈值计算
    threshold(cornerStrength, cornerMap, th, 255, THRESH_BINARY);
    cornerMap.convertTo(cornerMap, CV_8U);
    // 逐点的位运算
    bitwise_and(cornerMap, locaMax, cornerMap);

    drawCornerOnImage(image, cornerMap);
    namedWindow("result");
    imshow("result", image);
    waitKey();

    return 0;
}
void drawCornerOnImage(Mat& image, const Mat&binary)
{
    Mat_<uchar>::const_iterator it = binary.begin<uchar>();
    Mat_<uchar>::const_iterator itd = binary.end<uchar>();
    for (int i = 0; it != itd; it++, i++)
    {
        if (*it)
            circle(image, Point(i%image.cols, i / image.cols), 3, Scalar(0, 255, 0), 1);
    }
}

现在我们得到的效果就比默认的函数得到的结果有相当的改善，如上面最右边效果图。

 

3. 多尺度Harris角点

3.1 多尺度Harris角点的原理

虽然Harris角点检测算子具有部分图像灰度变化的不变性和旋转不变性，但它不具有尺度不变性。但是尺度不变性对图像特征来说至关重要。人们在使用肉眼识别物体时，不管物体远近，尺寸的变化都能认识物体，这是因为人的眼睛在辨识物体时具有较强的尺度不变性。在图像特征提取：尺度空间理论这篇文章里就已经讲到了高斯尺度空间的概念。

下面将Harris角点检测算子与高斯尺度空间表示相结合，使用Harris角点检测算子具有尺度的不变性。

 

多尺度Harris角点检测C++实现：https://github.com/RonnyYoung/ImageFeatures/blob/master/source/harrisLaplace.cpp

 

4. 更多的讨论

在上面描述的Harris角点具有光照不变性、旋转不变性、尺度不变性，但是严格意义上来说并不具备仿射不变性。

Harris-Affine是一种新颖的检测仿射不变特征点的方法，可以处理明显的仿射变换，包括大尺度变化和明显的视角变化。Harris-Affine主要是依据了以下三个思路：

1. 1. 特征点周围的二阶矩的计算对区域进行的归一化，具有仿射不变性；
   2. 通过在尺度空间上归一化微分的局部极大值求解来精化对应尺度；
   3. 自适应仿射Harris检测器能够精确定位牲点；

这篇文章不对Harris-Affine作进一步的描述，有时间会对这一算法做专门的分析，有兴趣的可以参考原论文：Scale & Affine Invariant Interest Point Detectors.

 

---

 

Simple Harris 的尺度不变性是个大弱点，所以便有了貌似气场无比牛逼的现代方法：

-- David Lowe

尺度不变特征变换 (SIFT)

1. 特征提取

　　显著特征，尺度不变性，旋转不变性，对光照基本不变性（关注的是对比度）

2. 特征描述

 

一种基于视觉单词的图像检索方法 理解SIFT的好文章，不吹。

 

算法简介

SIFT由David Lowe在1999年提出，在2004年加以完善[1-2]。SIFT在数字图像的特征描述方面当之无愧可称之为最红最火的一种，许多人对SIFT进行了改进，诞生了SIFT的一系列变种。SIFT已经申请了专利。

SIFT特征是基于物体上的一些局部外观的兴趣点而与影像的大小和旋转无关。

对于光线、噪声、微视角改变的容忍度也相当高。

基于这些特性，它们是高度显著而且相对容易撷取，在母数庞大的特征数据库中，很容易辨识物体而且鲜有误认。

使用SIFT特征描述对于部分物体遮蔽的侦测率也相当高，甚至只需要3个以上的SIFT物体特征就足以计算出位置与方位。

在现今的电脑硬件速度下和小型的特征数据库条件下，辨识速度可接近即时运算。SIFT特征的信息量大，适合在海量数据库中快速准确匹配。[5]

SIFT算法的特点 

 

SIFT算法具有如下一些特点：[5]

1.SIFT特征是图像的局部特征，其对旋转、尺度缩放、亮度变化保持不变性，对视角变化、仿射变换、噪声也保持一定程度的稳定性；

2. 独特性（Distinctiveness）好，信息量丰富，适用于在海量特征数据库中进行快速、准确的匹配；

3. 多量性，即使少数的几个物体也可以产生大量的SIFT特征向量；

4.高速性，经优化的SIFT匹配算法甚至可以达到实时的要求；

5.可扩展性，可以很方便的与其他形式的特征向量进行联合。

 

 

SIFT特征检测

SIFT特征检测主要包括以下4个基本步骤：

1. 尺度空间极值检测：

搜索所有尺度上的图像位置。通过高斯微分函数来识别潜在的对于尺度和旋转不变的兴趣点。

2. 关键点定位

在每个候选的位置上，通过一个拟合精细的模型来确定位置和尺度。关键点的选择依据于它们的稳定程度。

3. 方向确定

基于图像局部的梯度方向，分配给每个关键点位置一个或多个方向。所有后面的对图像数据的操作都相对于关键点的方向、尺度和位置进行变换，从而提供对于这些变换的不变性。

4. 关键点描述

在每个关键点周围的邻域内，在选定的尺度上测量图像局部的梯度。这些梯度被变换成一种表示，这种表示允许比较大的局部形状的变形和光照变化。

 

SIFT特征匹配

SIFT特征匹配主要包括2个阶段：

第一阶段：SIFT特征的生成，即从多幅图像中提取对尺度缩放、旋转、亮度变化无关的特征向量。

第二阶段：SIFT特征向量的匹配。

 

SIFT特征实现步骤

1. 构建尺度空间，检测极值点，获得尺度不变性。 

 

2. 特征点过滤并进行精确定位。

 

3. 为特征点分配方向值。 

 

4. 生成特征描述子。

以特征点为中心取16×16的邻域作为采样窗口，将采样点与特征点的相对方向通过高斯加权后归入包含8个bin的方向直方图，最后获得4×4×8的128维特征描述子。示意图如下：

当两幅图像的SIFT特征向量生成以后，下一步就可以采用关键点特征向量的欧式距离来作为两幅图像中关键点的相似性判定度量。

取图1的某个关键点，通过遍历找到图像2中的距离最近的两个关键点。

在这两个关键点中，如果次近距离除以最近距离小于某个阈值，则判定为一对匹配点。

SIFT特征匹配的例子：

 

 

待续。。。

 

---

 

 描述图像运动

 

 

// 七月份的博客内容以及下载的论文足以让本人对该area的知识体系有了一定的了解，但写博客与传统的记笔记相比，总是发现后者有更佳的效果，更适合个人的deep learning。遂，我要开始写笔记学习了。“好记性不如烂笔头”，望诸位亦能体会。