[OpenCV] Image Processing - Spatial Filtering
"利用给定像素周围的像素的值决定此像素的最终的输出值“
教学效果:

策略:
1. 拉普拉斯,突出小细节; 2. 梯度,突出边缘; 3. 平滑过的梯度图像用于掩蔽; 4. 灰度变换,增加灰度动态范围。
扩展阅读:
使用模糊技术进行 灰度变换 和 空间滤波 。
线性空间滤波

Some neighborhood operations (邻域算子):
(a) original image;
(b) blurred;
(c) sharpened;
(d) smoothed with edge-preserving filter;
(e) binary image;
(f) dilated;
(g) distance transform;
(h) connected components.
空间相关与卷积

离散单位冲击
一个函数与离散单位冲击相关,在该冲击位置产生这个函数的一个翻转版本。
一维卷积:R = g*f
二维卷积:R = G**H
扩展到二维图像 (二维滤波器)

卷积后重现了了卷积核的内容。
二维相关与卷积


w:脉冲响应函数
叠加原理 & 位移不变性原理

移不变线性系统对激励的响应可以由卷积得到。
可分离的滤波
核函数是否可分离?
http://www.isnowfy.com/introduction-to-svd-and-lsa/
数学问题,待续。。。
常用的滤波器

模糊核(平滑核)或低通核(通过 较低频信号 衰减 较高频信号)
- 减少高频噪声。
- 通过非锐化掩模处理,对图像进行锐化。
度量效果?傅立叶分析查看频率响应。待续。。。
线性滤波算子的其他功能:
-
- 边缘处理的预处理阶段,例如Sobel算子。
- 兴趣点检测,例如角点检测器。
高斯滤波

如果不是高斯噪声,怎么办?
中值滤波(统计排序滤波器)
散离噪声通常位于邻域内正确值的两端。

(a) original image with Gaussian noise; (b) Gaussian filtered; (c) median filtered; (d) bilaterally filtered; (e) original image with shot noise; (f) Gaussian filtered; (g) median filtered; (h) bilaterally filtered.
中值滤波、阿尔法截尾法中值滤波、加权法中值滤波。
滤波器大的保边效果好!而高斯滤波对边缘不好。但中值也好不到哪里去,对裂痕的平滑效果不好。
中值滤波适合去除椒盐噪声。
双边滤波器
同时考虑了像素和距离两个因素。
定义域核(c) 乘以 值域核(d)

双边滤波器中,输出像素的值依赖于邻域像素的值的加权组合,
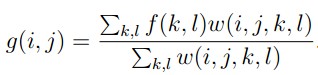
权重系数 w(i,j,k,l) 取决于定义域核
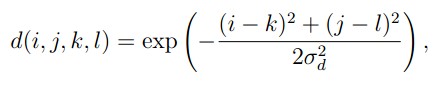
和值域核 (中间像素与邻域像素的矢量距离)
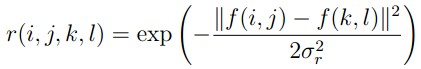
的乘积
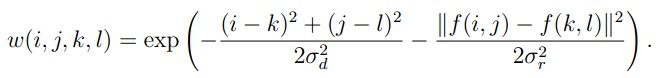
效果图:


高斯、中值、均值、双边滤波 (代码)

#include "cv.h" #include "highgui.h" #include <iostream> using namespace std; using namespace cv; int main(int argc, char* argv[]) { Mat src = imread("/home/unsw/lolo.jpg"); Mat dst; //参数是按顺序写的 //高斯滤波 //src:输入图像 //dst:输出图像 //Size(5,5)模板大小,为奇数 //x方向方差 //Y方向方差 GaussianBlur(src,dst,Size(5,5),0,0); imwrite("gauss.jpg",dst); //中值滤波 //src:输入图像 //dst::输出图像 //模板宽度,为奇数 medianBlur(src,dst,3); imwrite("med.jpg",dst); //均值滤波 //src:输入图像 //dst:输出图像 //模板大小 //Point(-1,-1):被平滑点位置,为负值取核中心 blur(src,dst,Size(3,3),Point(-1,-1)); imwrite("mean.jpg",dst); //双边滤波 //src:输入图像 //dst:输入图像 //滤波模板半径 //颜色空间标准差 //坐标空间标准差 bilateralFilter(src,dst,25, 25*2, 25/2); imwrite("bil.jpg",dst); waitKey(); return 0; }
噪声基础知识

1. 数字图像噪声的来源: 1)图像获取过程中; 2)图像信号传输过程中 2. 图像获取过程中产生的噪声: 1)主要受图像传感器的类型和质量影响:CCD采集图像过程中,受传感器材料属性、电子元器件和电路结构等影响,引入各种噪声,如 电阻引起的热噪声、 场效应管的沟道热噪声、 光子噪声、 暗电流噪声、 光响应非均匀性噪声 2)图像传感器的工作环境: 光照强度、 光照均匀度、 传感器温度 3. 图像传输过程中噪声: 主要由于传输信道被干扰而混入噪声 4. 噪声模型 1)使用随机过程的概率密度函数来描述 2)常见的噪声模型: a)高斯噪声; b)脉冲噪声 5. 高斯噪声 1)产生原因: a)图像传感器在拍摄时市场不够明亮、亮度不够均匀; b)电路各元器件自身噪声和相互影响; c)图像传感器长期工作,温度过高 2)在空间与和频域均为正态分布 6. 脉冲噪声 1)产生原因: 成像过程中的错误操作造成的 7. 去噪算法分类: 1)空间域去噪: a)均值去噪; b)顺序统计去噪(中值去噪、最大值去噪、最小值去噪、中点去噪、阿尔法均值去噪) 2)频率域去噪: a)针对固定频率噪声(带阻去噪、带通去噪、陷波去噪); b)针对噪声集中在高频区段(低通去噪) 3)小波去噪: 数学角度为函数逼近, 图像处理角度为低通去噪(对高频系数置零的线性去噪方法、基于阈值的小波去噪方法) 4)非局部均值去噪算法
锐化效果
导数和有限差分
有限差分估计导数,卷积核为:

但效果不好,因为快速变化是噪声的特点。
可以“先平滑”,再“差分操作”。


一阶微分 与 二阶微分

(1) 使用二阶微分进行图像锐化 -- 拉普拉斯Laplacian算子
拉普拉斯算子是最简单的各向同性微分算子,具有旋转不变性。一个二维图像函数 的拉普拉斯变换是各向同性的二阶导数,定义为:

以离散形式描述的话:(仔细体会这里的数学思想)

得到:
 (a)
(a)
然后,使用矩阵模板实现:

负值标注为0,为了之后与原图合并时保留背景信息。

(2) 使用“非锐化屏蔽“锐化
1. 模糊原图像
2. 从原图像中减去模板图像(产生的差值图像称为模板)
3. 将(模板*权值)加到原图像上。

(3) 使用一阶微分(梯度)对(非线性)图像锐化

指出了该像素点最大变化率的方向。
幅度值(长度)表示为M(x, y),即:

近似离散化为:

仍保留了灰度值的相对变化,但是通常各向同性特性丢失了。
(a) g的设计采用“罗伯特交叉梯度算子“:

那么,M(x, y) 得:

(b) 还可以采用“Sobel算子”:

那么,M(x, y) 得:
![]()
卷积模板设计:

特点:灰度不变或灰度变化缓慢的图案阴影被去除了。
(4) Laplacian of Gaussian 滤波器
带通滤波器
(1) 高斯滤波平滑

(2) Laplacian 算子

(1), (2) 等价于:

具有不错的尺度空间特性。
区域求和表(积分图像)
递归滤波器
无限脉冲响应(IIR)
有限脉冲响应(FIR)
计算“距离变换”

"曼哈顿距离"变换:通过两遍扫描的光栅算法(b), (c)。
(b)中的每个非0像素的值 == min(它北边 or 西边的邻域像素的距离+1)
逆向过程中,(b)中的每个非0像素的值 == min(此像素的值,它南边 or 东边的邻域像素的距离+1)
目的:获得内部达到最近边缘距离的信息(图)。
计算“连通量”
具有相同输入值(标签)的邻接像素的区域。

意义:

引伸:如何快速计算连通量?




 浙公网安备 33010602011771号
浙公网安备 33010602011771号