[ML] I'm back for Machine Learning

Hi, 

Long time no see. 

Briefly, I plan to step into this new area, data analysis. In the past few years, I have tried Linux programming, device driver development, android application development and RF SOC development. Thus, "data analysis become my fifth experience in IT field. This is not an easy technology if I want to be outstanding in coming two years. That's why I come back and look for the original power from blog. 

Time flies, I'm no longer the young guy with full energy. The only thing I would like to say to the rookie in their early 20s is "keep early hours and make valid plan". 

Good day!

 

Regards, 

/Jeff

Jupyter + Tensorflow + Nvidia GPU + Docker + Google Compute Engine

 

 

Ref: http://www.msra.cn/zh-cn/events/others/10years/79c3167b-b00c-43b8-ac56-4d3d1f895f2a.aspx

发这些论文的另外一个好处是吸引了很多好学生，这些年我见过很多非常优秀的学生，有些已不能用优秀来形容，只能说是天才。晓刚[5]是我见到的第一个天才学生，在硕士阶段就发表了五篇CVPR/ICCV。他的才华和人品如此出众，以至于我毫不犹豫地将妹妹嫁给了他。后来我的另一个天才级学生达华[6]发表了更多的文章，可是我已经没有妹妹可以再嫁了。好在最近的一个天才级学生靖宇[7]，来的时候就有女朋友了。靖宇编程打字的速度是如此之快，以至于我看不清他在键盘上快速移动的手。这三个学生共同特点是都收到MIT 和斯坦福的全额奖学金。晓刚和达华去了MIT，靖宇选择了斯坦福。我有种感觉，将来他们都会非常成功，成为各自领域的“天下第一铭”。我有种感觉，他们会越来越多。我更有种感觉，铭铭不属于他们。

 

作者介绍：汤晓鸥教授，是汤之铭的爸爸。1990年于中国科学技术大学获学士学位，1996年于麻省理工学院(MIT)获博士学位。现于香港中文大学信息工程系任终身教授。2005到2007年，于微软亚洲研究院担任视觉计算组主任。现任IEEE ICCV’09程序委员会主席 (Program Chair)及IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI)编委 (Associate Editor)。他的研究领域包括计算机视觉、模式识别、及视频处理。

晓鸥在亚洲研究院期间，被一致推选为研究院文工团团长，兼团委书记，连续三年出任研究院年度文艺晚会主持人，他的演艺生涯开始于研究院，也是在研究院达到顶峰，为此，他为自己起了个艺名叫“小o”，在研究院引起很大反响和误会，其正确发音应为Xiao Ou, 而不是“小圈”，“小圆”，“小饼”，“小豆”，“小球”，“小轮”，“小零”，或“小句号”。 小o的名言是：“看事物要一分为二，任何事物都有两个方面，有可笑的一面，同时也有更可笑的一面”。他就是这样看着铭铭一天天长大。

[1] SIGCHI: Special Interest Group for Computer Human Interaction，是世界上人机交互领域最大的专业组织，这是一个多学科交叉的学术组织，包括计算机科学家、软件工程师、心理学家、 交互设计人员、图形设计人员、社会学家和人类学家等等。大家共同理念是"设计有用且可用的技术是一个多学科交叉的过程，这一过程的恰当实施可以改变人们的生活"。

[2] ICCV: International Conference on Computer Vision，由IEEE主办的国际计算机视觉大会。作为世界顶级的学术会议，首届国际计算机视觉大会于1987年在伦敦揭幕，其后两年举办一届。2005年第10届ICCV在北京举行。

[3] CVPR: Computer Vision and Pattern Recognition，由IEEE主办的国际计算机视觉与模式识别大会，它是计算机视觉领域最顶级的三大学术会议之一。

[4] ECCV: European Conference on Computer Vision，两年举办一次，是计算机视觉领域三大顶级学术会议之一。

[5] 王晓刚：中国科大本科毕业，少年班第一名，郭沫若奖学金获得者，于香港中文大学取得硕士学位，现于麻省理工学院攻读博士学位。

[6] 林达华：中国科大本科毕业，于香港中文大学取得硕士学位，获香港中文大学工程院优秀硕士论文奖（每年度全院只选一人），现于麻省理工学院攻读博士学位。

[7] 崔靖宇：清华大学本科及硕士毕业，随汤晓鸥在研究院做了一年半的实习生，获微软学者奖学金，现于斯坦福大学攻读博士学位。

 

Jeff: 第一次读这篇文章是在三年前，那时除了老崔其他各位都显得陌生。接触该领域有段时间，三年后回头再看，原来文章中涉及的各位就是我一直研读论文的作者们，莫名的有了一种亲近感。冥冥中，妙不可言。

---

 

From: Computer Vision的尴尬 - 林达华

我不打算具体讨论一个topic，但是，我建议做vision的朋友在有时间的时候去看看一些表面应用完全不同，但是核心学理却是相通的领域。

• 做Sampling, particle filtering的，不妨看看统计物理学(Statistical Physics），他们对于蒙特卡罗方法已经应用数十年，积累极深，很可能在vision或者learning提出的一些新方法，已经是被他们以另外一种形式或者名称提出过了。
• 做Tracking, video, 和optimization的，可以看看控制论(Control theory)。控制科学对于动态系统（或者其它随时间变化的过程）的研究极为透彻。Alan本来是做控制的，正是他几次强烈的建议下，我才去看动态系统论和控制论，看过一些章节后有如醍醐灌顶。我曾经自己花了不少时间导出的一组矩阵微分方程的解，就是control theory里面已有深入探讨的Peano-Baker series在一定条件下的形式。至于做传导模型或者semi-supervised learning的，控制论中的许多观点和方法也是很有帮助的。
• 做Graphical model，和各种统计模型的，信息论(information theory)是肯定必要的，这个不用我在这啰嗦了。有一门叫做信息几何学(information geometry)，也值得一观。

 

林达华推荐的几本数学书

1. 线性代数 (Linear Algebra)：

我在科大一年级的时候就学习了这门课，后来到了香港后，又重新把线性代数读了一遍，所读的是

Introduction to Linear Algebra (3rd Ed.)  by Gilbert Strang.

这本书是MIT的线性代数课使用的教材，也是被很多其它大学选用的经典教材。它的难度适中，讲解清晰，重要的是对许多核心的概念讨论得比较透彻。

我个人觉得，学习线性代数，最重要的不是去熟练矩阵运算和解方程的方法——这些在实际工作中MATLAB可以代劳，关键的是要深入理解几个基础而又重要的概念：

• 子空间(Subspace)，
• 正交(Orthogonality)，
• 特征值
• 特征向量(Eigenvalues and eigenvectors)
• 线性变换(Linear transform)。

 

从我的角度看来，一本线代教科书的质量，就在于它能否给这些根本概念以足够的重视，能否把它们的联系讲清楚。Strang的这本书在这方面是做得很好的。

而且，这本书有个得天独厚的优势。书的作者长期在MIT讲授线性代数课(18.06)，课程的video在MIT的Open courseware网站上有提供。有时间的朋友可以一边看着名师授课的录像，一边对照课本学习或者复习。

http://ocw.mit.edu/OcwWeb/Mathematics/18-06Spring-2005/CourseHome/index.htm

 

2. 概率和统计 (Probability and Statistics):

概率论和统计的入门教科书很多，我目前也没有特别的推荐。我在这里想介绍的是一本关于多元统计的基础教科书：

Applied Multivariate Statistical Analysis (5th Ed.)  by Richard A. Johnson and Dean W. Wichern

这本书是我在刚接触向量统计的时候用于学习的，我在香港时做研究的基础就是从此打下了。实验室的一些同学也借用这本书学习向量统计。这本书没有特别追求数学上的深度，而是以通俗易懂的方式讲述主要的基本概念，读起来很舒服，内容也很实用。对于Linear regression, factor analysis, principal component analysis (PCA), and canonical component analysis (CCA)这些Learning中的基本方法也展开了初步的论述。

 

之后就可以进一步深入学习贝叶斯统计和Graphical models。一本理想的书是

Introduction to Graphical Models (draft version).  by M. Jordan and C. Bishop.

我不知道这本书是不是已经出版了（不要和Learning in Graphical Models混淆，那是个论文集，不适合初学）。这本书从基本的贝叶斯统计模型出发一直深入到复杂的统计网络的估计和推断，深入浅出，statistical learning的许多重要方面都在此书有清楚论述和详细讲解。MIT内部可以access，至于外面，好像也是有电子版的。

 

3. 分析 (Analysis)：

我想大家基本都在大学就学过微积分或者数学分析，深度和广度则随各个学校而异了。这个领域是很多学科的基础，值得推荐的教科书莫过于

Principles of Mathematical Analysis, by Walter Rudin

有点老，但是绝对经典，深入透彻。缺点就是比较艰深——这是Rudin的书的一贯风格，适合于有一定基础后回头去看。

 

在分析这个方向，接下来就是泛函分析(Functional Analysis)。

Introductory Functional Analysis with Applications, by Erwin Kreyszig.

适合作为泛函的基础教材，容易切入而不失全面。我特别喜欢它对于谱论和算子理论的特别关注，这对于做learning的研究是特别重要的。Rudin也有一本关于functional analysis的书，那本书在数学上可能更为深刻，但是不易于上手，所讲内容和learning的切合度不如此书。

 

在分析这个方向，还有一个重要的学科是测度理论(Measure theory)，但是我看过的书里面目前还没有感觉有特别值得介绍的。

 

4. 拓扑 (Topology)：

在我读过的基本拓扑书各有特色，但是综合而言，我最推崇：

Topology (2nd Ed.)  by James Munkres

这本书是Munkres教授长期执教MIT拓扑课的心血所凝。对于一般拓扑学(General topology)有全面介绍，而对于代数拓扑(Algebraic topology)也有适度的探讨。

此书不需要特别的数学知识就可以开始学习，由浅入深，从最基本的集合论概念（很多书不屑讲这个）到Nagata-Smirnov Theorem和Tychonoff theorem等较深的定理（很多书避开了这个）都覆盖了。

讲述方式思想性很强，对于很多定理，除了给出证明过程和引导你思考其背后的原理脉络，很多令人赞叹的亮点——我常读得忘却饥饿，不愿释手。很多习题很有水平。

 

5. 流形理论 (Manifold theory)：

对于拓扑和分析有一定把握时，方可开始学习流形理论，否则所学只能流于浮浅。我所使用的书是

Introduction to Smooth Manifolds.  by John M. Lee

虽然书名有introduction这个单词，但是实际上此书涉入很深，除了讲授了基本的manifold, tangent space, bundle, sub-manifold等，还探讨了诸如纲理论(Category theory)，德拉姆上同调(De Rham cohomology)和积分流形等一些比较高级的专题。

对于李群和李代数也有相当多的讨论。行文通俗而又不失严谨，不过对某些记号方式需要熟悉一下。

 

虽然李群论是建基于平滑流形的概念之上，不过，也可能从矩阵出发直接学习李群和李代数——这种方法对于急需使用李群论解决问题的朋友可能更加实用。而且，对于一个问题从不同角度看待也利于加深理解。下面一本书就是这个方向的典范：

Lie Groups, Lie Algebras, and Representations: An Elementary Introduction.  by Brian C. Hall

此书从开始即从矩阵切入，从代数而非几何角度引入矩阵李群的概念。并通过定义运算的方式建立exponential mapping，并就此引入李代数。这种方式比起传统的通过“左不变向量场(Left-invariant vector field)“的方式定义李代数更容易为人所接受，也更容易揭示李代数的意义。

最后，也有专门的论述把这种新的定义方式和传统方式联系起来。

 

 

Learning中的代数结构的建立

Learning是一个融会多种数学于一体的领域。说起与此有关的数学学科，我们可能会迅速联想到线性代数以及建立在向量空间基础上的统计模型——事实上，主流的论文中确实在很大程度上基于它们。

R^n (n-维实向量空间) 是我们在paper中见到最多的空间，它确实非常重要和实用，但是，仅仅依靠它来描述我们的世界并不足够。事实上，数学家们给我们提供了丰富得多的工具。

 

“空间”(space)，这是一个很有意思的名词，几乎出现在所有的数学分支的基础定义之中。归纳起来，所谓空间就是指一个集合以及在上面定义的某种数学结构。关于这个数学结构的定义或者公理，就成为这个数学分支的基础，一切由此而展开。

还是从我们最熟悉的空间——R^n 说起吧。大家平常使用这个空间的时候，除了线性运算，其实还用到了别的数学结构，包括度量结构和内积结构。

• 第一，它是一个拓扑空间(Topological space)。而且从拓扑学的角度看，具有非常优良的性质：Normal (implying Hausdorff and Regular), Locally Compact, Paracompact, with Countable basis, Simply connected (implying connected and path connected), Metrizable. 
• 第二，它是一个度量空间(Metric space)。我们可以计算上面任意两点的距离。
• 第三，它是一个有限维向量空间(Finite dimensional space)。因此，我们可以对里面的元素进行代数运算（加法和数乘），我们还可以赋予它一组有限的基，从而可以用有限维坐标表达每个元素。
• 第四，基于度量结构和线性运算结构，可以建立起分析(Analysis)体系。我们可以对连续函数进行微分，积分，建立和求解微分方程，以及进行傅立叶变换和小波分析。
• 第五，它是一个希尔伯特空间（也就是完备的内积空间）(Hilbert space, Complete inner product space)。它有一套很方便计算的内积(inner product)结构——这个空间的度量结构其实就是从其内积结构诱导出来。更重要的，它是完备的(Complete)——代表任何一个柯西序列(Cauchy sequence)都有极限——很多人有意无意中其实用到了这个特性，不过习惯性地认为是理所当然了。
• 第六，它上面的线性映射构成的算子空间仍旧是有限维的——一个非常重要的好处就是，所有的线性映射都可以用矩阵唯一表示。特别的，因为它是有限维完备空间，它的泛函空间和它本身是同构的，也是R^n。因而，它们的谱结构，也就可以通过矩阵的特征值和特征向量获得。
• 第七，它是一个测度空间——可以计算子集的大小（面积/体积）。正因为此，我们才可能在上面建立概率分布(distribution)——这是我们接触的绝大多数连续统计模型的基础。

我们可以看到，这是一个非常完美的空间，为我们的应用在数学上提供了一切的方便，在上面，我们可以理所当然地认为它具有我们希望的各种良好性质，而无须特别的证明；我们可以直接使用它的各种运算结构，而不需要从头建立；而且很多本来不一样的概念在这里变成等价的了，我们因此不再需要辨明它们的区别。

 

以此为界，Learning的主要工作分成两个大的范畴：

1. 建立一种表达形式，让它处于上面讨论的R^n空间里面。　　<----

2. 获得了有限维向量表达后，建立各种代数算法或者统计模型进行分析和处理。

 

这里只讨论第一个范畴。先看看，目前用得比较广泛的一些方法：

1.    直接基于原始数据建立表达

我们关心的最终目标是一个个现实世界中的对象：一幅图片，一段语音，一篇文章，一条交易记录，等等。这些东西大部分本身没有附着一个数值向量的。

为了构造一个向量表达，我们可以把传感器中记录的数值，或者别的什么方式收集的数值数据按照一定的顺序罗列出来，就形成一个向量了。如果有n个数字，就认为它们在R^n里面。

 

不过，这在数学上有一点小问题，在大部分情况下，根据数据产生的物理原理，这些向量的值域并不能充满整个空间。比如图像的像素值一般是正值，而且在一个有界闭集之中。这带来的问题是，对它们进行线性运算很可能得到的结果会溢出正常的范围——在大部分paper中，可能只是采用某些heuristics的手段进行简单处理，或者根本不管，很少见到在数学上对此进行深入探讨的——不过如果能解决实际问题，这也是无可厚非的，毕竟不是所有的工作都需要像纯数学那样追求严谨。

 

2.    量化(quantization)

这是在处理连续信号时被广泛采用的方式。只是习以为常，一般不提名字而已。比如一个空间信号（Vision中的image）或者时间信号，它们的domain中的值是不可数无限大的(uncountably infinite)，不要说表示为有限维向量，即使表达为无限序列也是不可能的。在这种情况下，一般在有限域内，按照一定顺序每隔一定距离取一个点来代表其周围的点，从而形成有限维的表达。这就是信号在时域或空域的量化。

这样做不可避免要丢失信息。但是，由于小邻域内信号的高度相关，信息丢失的程度往往并不显著。而且，从理论上说，这相当于在频域中的低通过率。对于有限能量的连续信号，不可能在无限高的频域中依然保持足够的强度，只要采样密度足够，丢失的东西可以任意的少。

除了表示信号，对于几何形体的表达也经常使用量化，比如表示curve和surface。

 

3.    找出有限个数充分表达一个对象也许不是最困难的。不过,在其上面建立数学结构却未必了

一般来说，我们要对其进行处理，首先需要一个拓扑结构用以描述空间上的点是如何联系在一起。直接建立拓扑结构在数学上往往非常困难，也未必实用。

因此，绝大部分工作采取的方式是首先建立度量结构。一个度量空间，其度量会自然地诱导出一个拓扑结构——不过，很多情况下我们似乎会无视它的存在。

最简单的情况，就是使用原始向量表达的欧氏距离(Euclidean distance)作为metric。不过，由于原始表达数值的不同特性，这种方式效果一般不是特别好，未必能有效表达实际对象的相似性（或者不相似性）。因此，很多工作会有再此基础上进行度量的二次建立。

方式是多种多样的，

　　(1) 一种是寻求一个映射，把原空间的元素变换到一个新的空间，在那里欧氏距离变得更加合适。这个映射发挥的作用包括对信息进行筛选，整合，对某些部分进行加强或者抑制。这就是大部分关于feature selection，feature extraction，或者subspace learning的文章所要做的。

　　(2) 另外一种方式，就是直接调节距离的计算方式（有些文章称之为metric learning）。

这两种方式未必是不同的。如果映射是单射，那么它相当于在原空间建立了一个不同的度量。反过来，通过改变距离计算方式建立的度量在特定的条件下对应于某种映射。

 

4.    大家可能注意到，上面提到的度量建立方法，比如欧氏距离，它需要对元素进行代数运算

对于普通的向量空间，线性运算是天然赋予的，我们无须专门建立，所以可以直接进行度量的构造——这也是大部分工作的基础。

可是，有些事物其原始表达不是一个n-tuple，它可能是一个set，一个graph，或者别的什么特别的object。怎么建立代数运算呢？

 

一种方法是直接建立。就是给这些东西定义自己的加法和数乘。这往往不是那么直接（能很容易建立的线性运算结构早已经被建立好并广泛应用了），可能需要涉及很深的数学知识，并且要有对问题本身的深入了解和数学上的洞察力。

不过，一个新的代数结构一旦建立起来，其他的数学结构，包括拓扑，度量，分析，以及内积结构也随之能被自然地诱导出来，我们也就具有了对这个对象空间进行各种数学运算和操作的基础。

加法和数乘看上去简单，但是如果我们对于本来不知道如何进行加法和数乘的空间建立了这两样东西，其理论上的贡献是非常大的。

（一个小问题：大家常用各种graphical model，但是，每次这些model都是分别formulate，然后推导出estimation和evaluation的步骤方法。是否可能对"the space of graphical model"或者它的某个特定子集建立某种代数结构呢？（不一定是线性空间，比如群，环，广群， etc）从而使得它们在代数意义上统一起来，而相应的estimation或者evaluation也可以用过代数运算derive。这不是我的研究范围，也超出了我目前的能力和知识水平，只是我相信它在理论上的重要意义，留作一个远景的问题。事实上，数学中确实有一个分支叫做 Algebraic statistics 可能在探讨类似的问题，不过我现在对此了解非常有限。）

 

5.    回到我们的正题，除了直接建立运算定义，另外一种方式就是嵌入(embedding)到某个向量空间，从而继承其运算结构为我所用

当然这种嵌入也不是乱来，它需要保持原来这些对象的某种关系。最常见的就是保距嵌入(isometric embedding)，

• • 首先建立度量结构（绕过向量表达，直接对两个对象的距离通过某种方法进行计算），
  • 然后把这个空间嵌入到目标空间，通常是有限维向量空间，要求保持度量不变。

“嵌入”是一种在数学上应用广泛的手段，其主要目标就是通过嵌入到一个属性良好，结构丰富的空间，从而利用其某种结构或者运算体系。

在拓扑学中，嵌入到metric space是对某个拓扑空间建立度量的重要手段。

而在这里，我们是已有度量的情况下，通过嵌入获取线性运算的结构。除此以来，还有一种就是前些年比较热的manifold embedding，这个是通过保持局部结构的嵌入，获取全局结构，后面还会提到。

 

6.    接下来的一个重要的代数结构，就是内积(inner product)结构

内积结构一旦建立，会直接诱导出一种性质良好的度量，就是范数(norm)，并且进而诱导出拓扑结构。

一般来说，内积需要建立在线性空间的基础上，否则连一个二元运算是否是内积都无法验证。不过，kernel理论指出，对于一个空间，只要定义一个正定核(positive kernel)——一个符合正定条件的二元运算，就必然存在一个希尔伯特空间（完备的内积空间），其内积运算等效于核运算。

这个结论的重要意义在于，我们可以绕开线性空间，通过首先定义kernel的方式，诱导出一个线性空间(叫做再生核希尔伯特空间 Reproducing Kernel Hilbert Space)，从而我们就自然获得我们所需要的度量结构和线性运算结构。这是kernel theory的基础。

在很多教科书中，以二次核为例子，把二维空间变成三维，然后告诉大家kernel用于升维。对于这种说法，我一直认为在一定程度上是误导的。事实上，kernel的最首要意义是内积的建立（或者改造），从而诱导出更利于表达的度量和运算结构。对于一个问题而言，选择一个切合问题的kernel比起关注“升维”来得更为重要。

kernel被视为非线性化的重要手段，用于处理非高斯的数据分布。这是有道理的。通过nonlinear kernel改造的内积空间，其结构和原空间的结构确实不是线性关联，从这个意义上说，它实施了非线性化。

不过，我们还应该明白，它的最终目标还是要回到线性空间，新的内积空间仍旧是一个线性空间，它一旦建立，其后的运算都是线性的，

因此，kernel的使用就是为了寻求一个新的线性空间，使得线性运算更加合理——非线性化的改造最终仍旧是要为线性运算服务。

值得一提的是，kernelization本质上说还是一种嵌入过程：对于一个空间先建立内积结构，并且以保持内积结构不变的方式嵌入到一个高维的线性空间，从而继承其线性运算体系。

 

7.    以局部而达全局——这就是流形(manifold)的思想，而其则根源于拓扑学

上面说到的都是从全局的方式建立代数结构的过程，但是那必须以某种全局结构为基础（无论预先定义的是运算，度量还是内积，都必须适用于全空间。）

但是，全局结构未必存在或者适合，而局部结构往往简单方便得多。这里就形成一种策略，以局部而达全局——这就是流形(manifold)的思想，而其则根源于拓扑学。

 

从拓扑学的角度说，流形就是一个非常优良的拓扑空间：符合Hausdorff分离公理（任何不同的两点都可以通过不相交的邻域分离），符合第二可数公理（具有可数的拓扑基），并且更重要的是，局部同胚于R^n。

因此，一个正则(Regular)流形基本就具有了各种最良好的拓扑特性。

而局部同胚于R^n，代表了它至少在局部上可以继承R^n的各种结构，比如线性运算和内积，从而建立分析体系。

事实上，拓扑流形继承这些结构后形成的体系，正是现代流形理论研究的重点。

继承了分析体系的流形，就形成了微分流形(Differential manifold)，这是现代微分几何的核心。

而微分流形各点上的切空间(Tangent Space)，则获得了线性运算的体系。

而进一步继承了局部内积结构的流形，则形成黎曼流形(Riemann manifold)，而流形的全局度量体系——测地距离(geodesics)正是通过对局部度量的延伸来获得。

进一步的，当流行本身的拓扑结构和切空间上的线性结构发生关系——也就获得一簇拓扑关联的线性空间——向量丛(Vector bundle)。

 

虽然manifold theory作为现代几何学的核心，是一个博大精深的领域，但是它在learning中的应用则显得非常狭窄。

事实上，对于manifold，很多做learning的朋友首先反应的是ISOMAP, LLE, eigenmap之类的算法。这些都属于embedding。

当然，这确实是流形理论的一个重要方面。严格来说，这要求是从原空间到其映像的微分同胚映射，因此，嵌入后的空间在局部上具有相同的分析结构，同时也获得了各种好处——全局的线性运算和度量。

不过，这个概念在learning的应用中被相当程度的放宽了——微分同胚并不能被完全保证，而整个分析结构也不能被完全保持。大家更关注的是保持局部结构中的某个方面——不过这在实际应用中的折衷方案也是可以理解的。

事实表明，当原空间中的数据足够密集的情况下，这些算法工作良好。

 

Learning中流形应用的真正问题在于它被过滥地运用于稀疏空间(Sparse space)，事实上在高维空间中撒进去几千乃至几十万点，即使最相邻的几点也难称为局部了，局部的范围和全局的范围其实已经没有了根本差别，连局部的概念都立不住脚的时候，后面基于其展开的一切工作也都没有太大的意义。

事实上，稀疏空间有其本身的规律和法则，通过局部形成全局的流形思想从本质上是不适合于此的。虽然，流形是一种非常美的理论，但是再漂亮的理论也需要用得其所——它应该用于解决具有密集数据分布的低维空间。至于，一些paper所报告的在高维空间（比如人脸）运用流形方法获得性能提升，其实未必是因为“流形”本身所起的作用，而很可能是其它方面的因素。

 

8.    流形应用

流形在实际应用中起重要作用的还有两个方面：

一个是研究几何形体的性质（我们暂且不谈这个），

还有就是它和代数结构的结合形成的李群(Lie group)和李代数(Lie algebra)。

 

当我们研究的对象是变换本身的时候，它们构成的空间是有其特殊性的，比如所有子空间投影形成了Grassmann流形，所有的可逆线性算子，或者仿射算子，也形成各自的流形。对他们的最重要操作是变换的结合，而不是加法数乘，因此，它们上面定义的更合适的代数结构应该是群和不是线性空间。而群和微分流形的结合体——李群则成为它们最合适的描述体系——而其切空间则构成了一种加强的线性空间：李代数，用于描述其局部变化特性。

李代数和李群的关系是非常漂亮的。它把变换的微变化转换成了线性空间的代数运算，使得移植传统的基于线性空间的模型和算法到李空间变得可能。而且李代数中的矩阵比起变换本身的矩阵甚至更能反映变换的特性。几何变换的李代数矩阵的谱结构就能非常方便地用于分析变换的几何特性。

 

 

最后，回头总结一下关于嵌入这个应用广泛的策略，在learning中的isometry, kernel和manifold embedding都属于此范畴，它们分别通过保持原空间的度量结构，内积结构和局部结构来获得到目标（通常是向量空间）的嵌入，从而获得全局的坐标表达，线性运算和度量，进而能被各种线性算法和模型所应用。

在获得这一系列好处的同时，也有值得我们注意的地方。

• 首先，嵌入只是一种数学手段，并不能取代对问题本身的研究和分析。一种不恰当的原始结构或者嵌入策略，很多时候甚至适得其反——比如稀疏空间的流形嵌入，或者选取不恰当的kernel。
• 另外，嵌入适合于分析，而未必适合于重建或者合成。这是因为嵌入是一个单射(injection)，目标空间不是每一个点都和原空间能有效对应的。嵌入之后的运算往往就打破了原空间施加的限制。比如两个元素即使都是从原空间映射过来，它们的和却未必有原像，这时就不能直接地回到原空间了。当然可以考虑在原空间找一个点它的映射与之最近，不过这在实际中的有效性是值得商榷的。

 

和Learning有关的数学世界是非常广博的，我随着学习和研究的深入，越来越发现在一些我平常不注意的数学分支中有着适合于问题的结构和方法。

比如，广群(groupoid)和广代数(algebroid)能克服李群和李代数在表示连续变换过程中的一些困难——这些困难困扰了我很长时间。

解决问题和建立数学模型是相辅相成的，

一方面，一个清晰的问题将使我们有明确的目标去寻求合适的数学结构，

另一方面，对数学结构的深入理解对于指导问题的解决也是有重要作用的。

 

对于解决一个问题来说，数学工具的选择最重要的是适合，而不是高深，但是如果在现有数学方法陷入困难的时候，寻求更高级别的数学的帮助，往往能柳暗花明。数学家长时间的努力解决的很多问题，并不都是理论游戏，他们的解决方案中很多时候蕴含着我们需要的东西，而且可能导致对更多问题的解决——但是我们需要时间去学习和发现它们。

 

 

拓扑：游走于直观与抽象之间

近日来，抽空再读了一遍点集拓扑(Point Set Topology)，这是我第三次重新学习这个理论了。我看电视剧和小说，极少能有兴致看第二遍，但是，对于数学，每看一次都有新的启发和收获。

代数，分析，拓扑，被称为是现代数学的三大柱石。

最初读拓扑，是在两三年前，由于学习流形理论的需要。可是，随着知识的积累，发现它是很多理论的根基。可以说，没有拓扑，就没有现代意义的分析与几何。我们在各种数学分支中接触到的最基本的概念，比如，极限，连续，距离（度量），边界，路径，在现代数学中，都源于拓扑。

拓扑学是一门非常奇妙的学科，它把最直观的现象和最抽象的概念联系在一起了。拓扑描述的是普遍使用的概念（比如开集，闭集，连续），我们对这些概念习以为常，理所当然地使用着，可是，真要定义它，则需要对它们本质的最深刻的洞察。数学家们经过长时间的努力，得到了这些概念的现代定义。这里面很多第一眼看上去，会感觉惊奇——怎么会定义成这个样子。

 

首先是开集。在学习初等数学时，我们都学习开区间 (a, b)。可是，这只是在一条线上的，怎么推广到二维空间，或者更高维空间，或者别的形体上呢？最直观的想法，就是“一个不包含边界的集合”。可是，问题来了，给一个集合，何谓“边界”？在拓扑学里面，开集(Open Set)是最根本的概念，它是定义在集合运算的基础上的。它要求开集符合这样的条件：开集的任意并集和有限交集仍为开集。

 

我最初的时候，对于这样的定义方式，确实百思不解。不过，读下去，看了和做了很多证明后，发现，这样的定义一个很重要的意义在于：它保证了开集中每个点都有一个邻域包含在这个集合内——所有点都和外界（补集）保持距离。这样的理解应该比使用集合运算的定义有更明晰的几何意义。但是，直观的东西不容易直接形成严谨的定义，使用集合运算则更为严格。而集合运算定义中，任意并集的封闭性是对这个几何特点的内在保证。

 

另外一个例子就是“连续函数”(Continuous Function)。在学微积分时，一个耳熟能详的定义是“对任意的epsilon > 0，存在delta > 0，使得。。。。”，背后最直观的意思就是“足够近的点保证映射到任意小的范围内”。可是，epsilon, delta都依赖于实空间，不在实空间的映射又怎么办呢？拓扑的定义是“如果一个映射的值域中任何开集的原象都是开集，那么它连续。”这里就没有epsilon什么事了。“开集的原象是开集”

 

这里的关键在于，在拓扑学中，开集的最重要意义就是要传递“邻域”的意思——开集本身就是所含点的邻域。

这样连续定义成这样就顺理成章了。稍微把说法调节一下，上面的定义就变成了“对于f(x)的任意邻域U，都有x的一个邻域V，使得V里面的点都映射到U中。”

 

这里面，我们可以感受到为什么开集在拓扑学中有根本性的意义。既然开集传达“邻域”的意思，那么，它最重要的作用就是要表达哪些点靠得比较近。给出一个拓扑结构，就是要指出哪些是开集，从而指出哪些点靠得比较近，这样就形成了一个聚集结构——这就是拓扑。

 

可是这也可以通过距离来描述，为什么要用开集呢，反而不直观了。某种意义上说，拓扑是“定性”的，距离度量是“定量”的。随着连续变形，距离会不断变化，但是靠近的点还是靠近，因此本身固有的拓扑特性不会改变。拓扑学研究的就是这种本质特性——连续变化中的不变性。

 

在拓扑的基本概念中，最令人费解的，莫过于“紧性”(Compactness)。它描述一个空间或者一个集合“紧不紧”。正式的定义是“如果一个集合的任意开覆盖都有有限子覆盖，那么它是紧的”。乍一看，实在有点莫名其妙。它究竟想描述一个什么东西呢？和“紧”这个形容词又怎么扯上关系呢？

一个直观一点的理解，几个集合是“紧”的，就是说，无限个点撒进去，不可能充分散开。无论邻域多么小，必然有一些邻域里面有无限个点。上面关于compactness的这个定义的玄机就在有限和无限的转换中。一个紧的集合，被无限多的小邻域覆盖着，但是，总能找到其中的有限个就能盖全。那么，后果是什么呢？无限个点撒进去，总有一个邻域包着无数个点。邻域们再怎么小都是这样——这就保证了无限序列中存在极限点。

 

Compact这个概念虽然有点不那么直观，可是在分析中有着无比重要的作用。因为它关系到极限的存在性——这是数学分析的基础。了解泛函分析的朋友都知道，序列是否收敛，很多时候就看它了。微积分中，一个重要的定理——有界数列必然包含收敛子列，就是根源于此。

在学习拓扑，或者其它现代数学理论之前，我们的数学一直都在有限维欧氏空间之中，那是一个完美的世界，具有一切良好的属性，Hausdorff, Locally compact, Simply connected，Completed，还有一套线性代数结构，还有良好定义的度量，范数，与内积。可是，随着研究的加深，终究还是要走出这个圈子。这个时候，本来理所当然的东西，变得不那么必然了。

• • 两个点必然能分开？你要证明空间是Hausdorff的。
  • 有界数列必然存在极限点？这只在locally compact的空间如此。
  • 一个连续体内任意两点必然有路径连接？这可未必。

一切看上去有悖常理，而又确实存在。从线性代数到一般的群，从有限维到无限维，从度量空间到拓扑空间，整个认识都需要重新清理。而且，这些绝非仅是数学家的概念游戏，因为我们的世界不是有限维向量能充分表达的。

当我们研究一些不是向量能表达的东西的时候，度量，代数，以及分析的概念，都要重新建立，而起点就在拓扑。

 

在数学的海洋中飘荡 - 达华

 

一些其他链接：

李群李代数与纤维丛

主讲人： 梁灿彬

主讲人单位：北京师范大学 

 

机器学习算法集锦

数学史

 

---

Brief History of Machine Learning

 

 

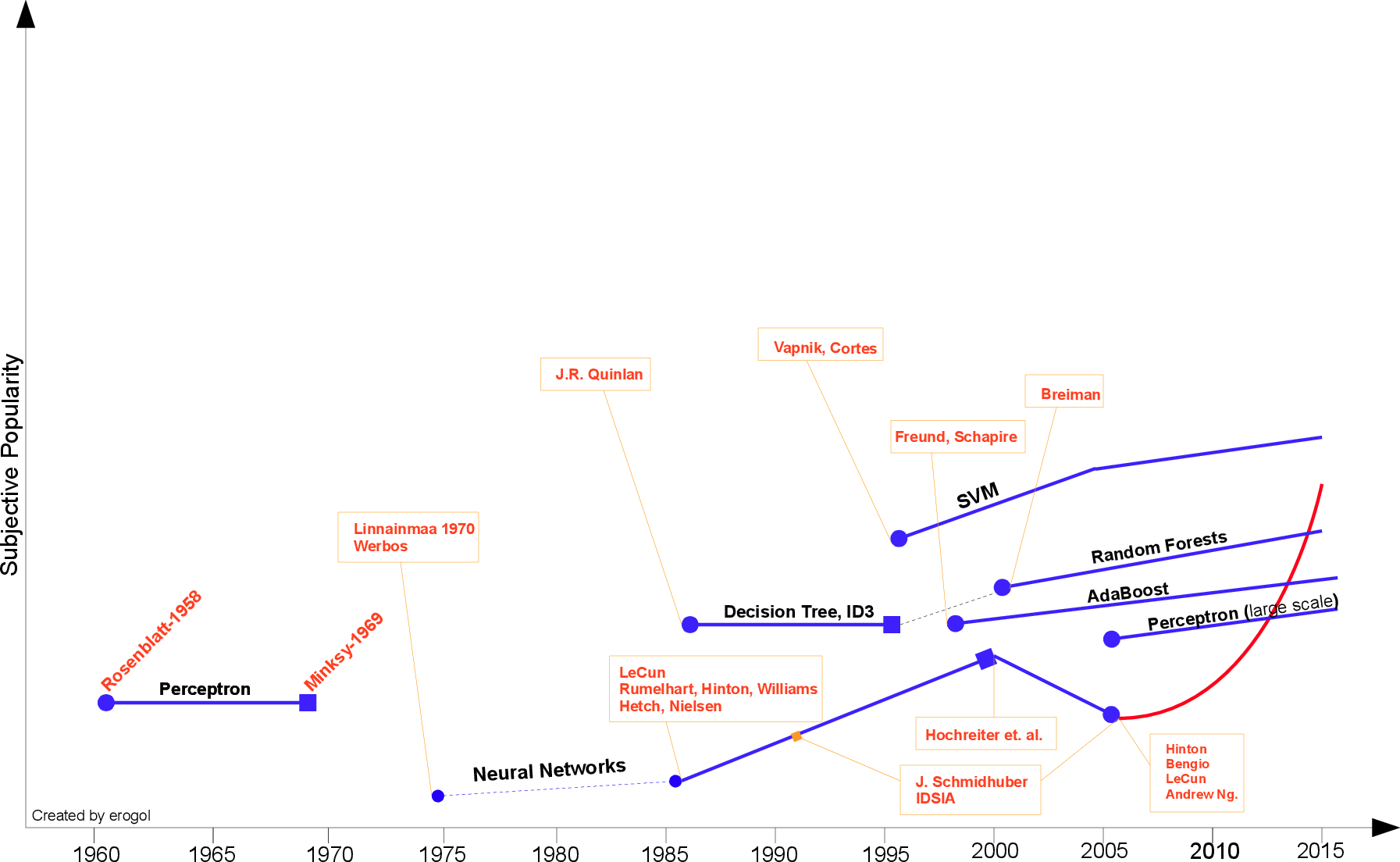
Hebb 在 1949 年基于神经心理的学习方式第一次提出了机器学习方法，该方法被称之为 Hebbian 学习理论。该学习理论通过简单的解释展示了循环神经网络（RNN）中结点之间的相关性关系。它记忆住神经网络上任何共性信息，就像后来的记忆一样。正式地，概念可以表述为下：

若我们假设持续或反复的反射活动（或「trace」）会倾向于引起持续的细胞变化，并增加其稳定性。那么当细胞 A 的轴突足够接近以激发细胞 B，然后反复或持续地激发它，就会在一个或两个细胞中发生一些生长过程或代谢改变，如 A 的效率在另一个细胞激发了 B 时提升 [1] 

 

1952 年 Arthur Samuel 在 IBM 开发了一款玩西洋棋的程序。该程序能够观察位置并学习一个隐式模型以在后一步棋中获得更好的策略。Samuel 用该程序下了许多盘棋，并发现程序最后能下得更好。

通过这个程序，Arthur Samuel 反驳了广义 providence 指令机不能超越所写的代码并学习类人模式这一观点。他还创造了「机器学习」这一术语，并定义为：

在没有明确指令的情况下赋予计算机能力的一个研究领域。

  

Rosenblatt 在 1957 年提出的感知机是拥有神经科学背景的第二个模型，该算法更像现在的机器学习模型。这一模型是十分重要的发现，实际上它要比 Hebbian 的想法更具适用性。Rosenblatt 通过下面的定义介绍了感知机模型：

感知机旨在说明一般智能系统的一些基本属性，它不会因为个别特例或通常不知道的东西所束缚住，也不会因为那些个别生物有机体的情况而陷入混乱。

 

在 3 年后，Widrow [4] 加上了 Delta 学习法则，该学习法则被用作感知机训练的可实践过程，其也通常称之为最小二乘问题。(delta法则的关键思想是利用梯度下降（gradient descent）来搜索可能的权向量的假设空间，以找到最佳拟合训练样例的权向量)

如果结合这两个观点，我们就能建立一个很好的线性分类器。

 

然而感知机的流行被 Minsky[3] 在 1969 年提出的问题所终止，他提出了著名的逻辑异或问题（XOR problem），并指出感知机在这种线性不可分的数据分布上是失效的。这是 Minsky 对神经网络社区的攻击，此后神经网络的研究者进入了寒冬，直到 1980 年才再一次复苏。

 

 

Minsky 后一段时间并没有什么研究结果，直到 Werbos[6] 1981 年在神经网络具体的反向传播（BP）算法中提出了多层感知机模型（MLP）才出现转机。

虽然 BP 算法的概念由 Linnainmaa [5] 在 1970 年就已经以「自动微分的反向模型」为名提出来了，但 BP 算法仍然是当今神经网络架构的重要组成部分。

有了这些新概念，神经网络的研究再一次加速。

 

在 1985-1986 年，研究者相继提出了使用 BP 算法训练的多参数线性规划（MLP）问题（Rumelhart, Hinton, Williams [7]—Hetch, Nielsen[8]）。

来自于 Hetch 和 Nielsen [8]

 

在另一个谱系中，J.R.Quinlan [9] 于 1986 年提出了一种非常出名的机器学习算法，我们称之为决策树，更具体的说是 ID3 算法。这是另一个主流机器学习算法的突破点。此外 ID3 算法也被发布成为了一款软件，它能以简单的规划和明确的推论找到更多的现实案例，而这一点正好和神经网络黑箱模型相反。

在 ID3 算法提出来以后，研究社区已经探索了许多不同的选择或改进（如 ID4、回归树、CART 算法等），这些算法仍然活跃在机器学习领域中。

  

最重要的机器学习突破之一是 Vapnik 和 Cortes[10] 在 1995 年提出的支持向量机（SVM），该算法具有非常强大的理论地位和实证结果。

那一段时间机器学习研究社区也分为 NN 和 SVM 两派。然而，在 2000 年左右提出了带核函数的支持向量机后，神经网络已经无力与其竞争。SVM 在许多以前由 NN 占据的任务中获得了更好的效果。此外，SVM 相对于 NN 还能利用所有关于凸优化、泛化边际理论和核函数的深厚知识。因此 SVM 可以从不同的学科中大力推动理论和实践的改进。

来自于 Vapnik 和 Cortes [10]

 

通过 1991 年 Hochreiter 的论文 [40] 和 Hochreiter et. al.[11] 在 2001 年的研究，神经网络遭受到又一个质疑。

因为他们的研究表明在我们应用 BP 算法学习时，NN 神经元饱和后会出现梯度损失（gradient loss）的情况。

简单地说，由于神经元饱和，在一定数量的 epochs 后训练的 NN 神经元是多余的，因此 NN 非常倾向于在小 epochs 数量上产生过拟合现象。

 

不久之后，Freund 和 Schapire 在 1997 年提出了另一个著名的机器学习模型，即利用多个弱分类器组合成强分类器的 Adaboost 算法。

该提升方法从弱学习算法出发，反复学习，得到一系列弱分类器（又称为基本分类器），然后组合这些弱分类器，构成一个强分类器。AdaBoost 通过改变训练数据的概率分布，针对不同的训练数据分布调用弱学习算法学习一系列弱分类器。AdaBoost 的做法是提高那些被前一轮弱分类器错误分类样本的权重。所以那些错误分类的样本由于其权重增加而会受到后一轮弱分类器的更大关注，从而利用多个弱分类器解决复杂问题。这种模型仍然是很多不同任务的基础，如面部识别和检测。它也是实现 PAC（Probably Approximately Correct）学习理论的方法。Freund 和 Schapire 将 Adaboost 算法描述为：

我们研究的模型可解释为将在线预测模型更宽、更抽象地扩展为通用的决策理论设定。

 

Breiman [12] 在 2001 年探索了另一种集成模型，该模型集成了多棵决策树，其中每一棵决策树都由样本的随机子集而构建，每一个结点都是从特征的随机子集中选择。由于该算法的性质，我们称之为随机森林（RF）。

RF 在过拟合耐性有理论和实证方面的证明。实际上 AdaBoost 显示了过拟合和数据中的异常值的缺点，而 RF 是针对这些缺点更具鲁棒性的模型。RF 在许多不同的任务，如 Kaggle 比赛中也取得了很多的成功。

随机森林是树型预测的组合，其中每棵树取决于独立采样的随机向量值，并且森林中所有的树都服从相同的分布。森林的泛化误差随着树的数量变多而收敛于一个极限值 [12]。

 

如今，NN 的一个新纪元由深度学习而引发。深度学习指具有许多广泛连续层的 NN 模型。

NN 模型的第三次崛起大概在 2005 年，其由最近的 Hinton、LeCun、Bengio、Andrew Ng 和其他研究员共同完成。

 

下面是一些深度学习重要的主题：

• GPU programming

• Convolutional NNs [18][20][40]

• Deconvolutional Networks [21] 反卷积网络

• Stochastic Gradient Descent [19][22]

• BFGS and L-BFGS [23] 拟牛顿法及其改进

• Conjugate Gradient Descent [24] 共轭梯度下降

• Backpropagation [40][19]

• Rectifier Units

• Sparsity [15][16] 稀疏性问题

• Dropout Nets [26]

• Maxout Nets [25] maxout 网络

• Unsupervised NN models [14] 非监督神经网络模型

• Deep Belief Networks [13] 深度置信网络

• Stacked Auto-Encoders [16][39] 栈式的自编码器

• Denoising NN models [17] 去噪神经网络模型

• (GAN) Generative Adversarial Networks [41] 生成式对抗网络

• Variational Auto-Encoders [42] 变分自编码器

 

AlexNet 赢得 ImageNet 挑战赛，深度学习起飞

 

结合以上列出的以及未列出的所有思路，神经网络模型能够在多种不同的人物上取得顶尖成果，例如目标识别、语音识别、NLP 等。然而，这并不意味着其他机器学习流派的终结。即使深度学习增长迅速，但深度学习所需要的训练成本、调整模型的大量参数上仍多有诟病。此外，SVM 因其简单性也有了更普遍的运用。

在深度学习潮流下，我们看到了图像识别要早于 NLP 成为了第一个突破点。这些问题看起来解决地很好，而且我们也看到了许多人工智能产品。

 

 

下一个趋势 :

看起来是在视频与生成式模型上面。

 

如果我们把人类视觉感知用时序输入来模拟，那么视频的输入量会变得更大，在计算和算法两方面也是个更难的问题，因此也就比一般的人工智能任务更重要。

生成式学习以倒序的方式处理问题，"给模型一定的线索，它会生成真实的图像"。这样的模型需要学习如何表达数据，而非只是进行分类。

 

这两种趋势都提供更智能的算法，并可能减少深度学习解决方案中所需要的大量数据。例如，有了视频输入，算法能够学习目标的多个不同方面，也能在没有 ImageNet 这样的大型数据集的情况下归纳这些信息。

生成式模型在数据稀缺的领域能很好的归纳表征知识，从而进行分类任务。

 

在结束之前，我想要提一下另外一个很热的机器学习话题。

随着互联网、社交媒体的兴起，大数据开始崛起并极大的影响着机器学习的研究。因为源自大数据的许多问题，众多强大的机器学习算法开始变得没用。

因此研究人员想出了一系列被称为 Bandit Algorithm 的新的简单模型（之前是在线学习），从而使得学习更简单、更适用于大规模问题。

我了个去，强盗算法！

 

参考文献

参考文献：

[1] Hebb D. O., The organization of behaviour.New York: Wiley & Sons.
[2]Rosenblatt, Frank. “The perceptron: a probabilistic model for information storage and organization in the brain.” Psychological review 65.6 (1958): 386.
[3]Minsky, Marvin, and Papert Seymour. “Perceptrons.” (1969).
[4]Widrow, Hoff “Adaptive switching circuits.” (1960): 96–104.
[5]S. Linnainmaa. The representation of the cumulative rounding error of an algorithm as a Taylor
 expansion of the local rounding errors. Master’s thesis, Univ. Helsinki, 1970.
[6] P. J. Werbos. Applications of advances in nonlinear sensitivity analysis. In Proceedings of the 10th
 IFIP Conference, 31.8–4.9, NYC, pages 762–770, 1981.
[7] Rumelhart, David E., Geoffrey E. Hinton, and Ronald J. Williams. Learning internal representations by error propagation. No. ICS-8506. CALIFORNIA UNIV SAN DIEGO LA JOLLA INST FOR COGNITIVE SCIENCE, 1985.
[8] Hecht-Nielsen, Robert. “Theory of the backpropagation neural network.” Neural Networks, 1989. IJCNN., International Joint Conference on. IEEE, 1989.
[9] Quinlan, J. Ross. “Induction of decision trees.” Machine learning 1.1 (1986): 81–106.
[10] Cortes, Corinna, and Vladimir Vapnik. “Support-vector networks.” Machine learning 20.3 (1995): 273–297.
[11] Freund, Yoav, Robert Schapire, and N. Abe. “A short introduction to boosting.”Journal-Japanese Society For Artificial Intelligence 14.771–780 (1999): 1612.
[12] Breiman, Leo. “Random forests.” Machine learning 45.1 (2001): 5–32.
[13] Hinton, Geoffrey E., Simon Osindero, and Yee-Whye Teh. “A fast learning algorithm for deep belief nets.” Neural computation 18.7 (2006): 1527–1554.
[14] Bengio, Lamblin, Popovici, Larochelle, “Greedy Layer-Wise
 Training of Deep Networks”, NIPS’2006
[15] Ranzato, Poultney, Chopra, LeCun “ Efficient Learning of Sparse Representations with an Energy-Based Model “, NIPS’2006
[16] Olshausen B a, Field DJ. Sparse coding with an overcomplete basis set: a strategy employed by V1? Vision Res. 1997;37(23):3311–25. Available at: http://www.ncbi.nlm.nih.gov/pubmed/9425546.
[17] Vincent, H. Larochelle Y. Bengio and P.A. Manzagol, Extracting and Composing Robust Features with Denoising Autoencoders, Proceedings of the Twenty-fifth International Conference on Machine Learning (ICML‘08), pages 1096–1103, ACM, 2008.
[18] Fukushima, K. (1980). Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biological Cybernetics, 36, 193–202.
[19] LeCun, Yann, et al. “Gradient-based learning applied to document recognition.”Proceedings of the IEEE 86.11 (1998): 2278–2324.
[20] LeCun, Yann, and Yoshua Bengio. “Convolutional networks for images, speech, and time series.” The handbook of brain theory and neural networks3361 (1995).
[21] Zeiler, Matthew D., et al. “Deconvolutional networks.” Computer Vision and Pattern Recognition (CVPR), 2010 IEEE Conference on. IEEE, 2010.
[22] S. Vishwanathan, N. Schraudolph, M. Schmidt, and K. Mur- phy. Accelerated training of conditional random fields with stochastic meta-descent. In International Conference on Ma- chine Learning (ICML ’06), 2006.
[23] Nocedal, J. (1980). ”Updating Quasi-Newton Matrices with Limited Storage.” Mathematics of Computation 35 (151): 773782. doi:10.1090/S0025–5718–1980–0572855-
[24] S. Yun and K.-C. Toh, “A coordinate gradient descent method for l1- regularized convex minimization,” Computational Optimizations and Applications, vol. 48, no. 2, pp. 273–307, 2011.
[25] Goodfellow I, Warde-Farley D. Maxout networks. arXiv Prepr arXiv …. 2013. Available at: http://arxiv.org/abs/1302.4389. Accessed March 20, 2014.
[26] Wan L, Zeiler M. Regularization of neural networks using dropconnect. Proc …. 2013;(1). Available at: http://machinelearning.wustl.edu/mlpapers/papers/icml2013_wan13.Accessed March 13, 2014.
[27] Alekh Agarwal, Olivier Chapelle, Miroslav Dudik, John Langford, A Reliable Effective Terascale Linear Learning System, 2011
[28] M. Hoffman, D. Blei, F. Bach, Online Learning for Latent Dirichlet Allocation, in Neural Information Processing Systems (NIPS) 2010.
[29] Alina Beygelzimer, Daniel Hsu, John Langford, and Tong ZhangAgnostic Active Learning Without Constraints NIPS 2010.
[30] John Duchi, Elad Hazan, and Yoram Singer, Adaptive Subgradient Methods for Online Learning and Stochastic Optimization, JMLR 2011 & COLT 2010.
[31] H. Brendan McMahan, Matthew Streeter, Adaptive Bound Optimization for Online Convex Optimization, COLT 2010.
[32] Nikos Karampatziakis and John Langford, Importance Weight Aware Gradient Updates UAI 2010.
[33] Kilian Weinberger, Anirban Dasgupta, John Langford, Alex Smola, Josh Attenberg, Feature Hashing for Large Scale Multitask Learning, ICML 2009.
[34] Qinfeng Shi, James Petterson, Gideon Dror, John Langford, Alex Smola, and SVN Vishwanathan, Hash Kernels for Structured Data, AISTAT 2009.
[35] John Langford, Lihong Li, and Tong Zhang, Sparse Online Learning via Truncated Gradient, NIPS 2008.
[36] Leon Bottou, Stochastic Gradient Descent, 2007.
[37] Avrim Blum, Adam Kalai, and John Langford Beating the Holdout: Bounds for KFold and Progressive Cross-Validation. COLT99 pages 203–208.
[38] Nocedal, J. (1980). “Updating Quasi-Newton Matrices with Limited Storage”. Mathematics of Computation 35: 773–782.
[39] D. H. Ballard. Modular learning in neural networks. In AAAI, pages 279–284, 1987.
[40] S. Hochreiter. Untersuchungen zu dynamischen neuronalen Netzen. Diploma thesis, Institut f ̈ur In-
 formatik, Lehrstuhl Prof. Brauer, Technische Universit ̈at M ̈unchen, 1991. Advisor: J. Schmidhuber.
[41] Goodfellow, Ian, et al. “Generative adversarial nets.” Advances in neural information processing systems. 2014.
[42] Diederik P Kingma. Auto-Encoding Variational Bayes https://arxiv.org/abs/1312.6114

 

附录：补充近期的研究热点

选自GitHub

作者：Simon Brugman

<从文本到视觉：各领域最前沿的论文集合>

目录

1. 文本
    1.1. 代码生成（Code Generation）
    1.2. 情感分析（Sentiment Analysis）
    1.3. 翻译（Translation）
    1.4. 分类（Classification）
2. 视觉
    2.1. 游戏（Gaming）
    2.2. 风格迁移（Style Transfer）
    2.3. 跟踪（Tracking）
    2.4. 图像分割（Image Segmentation）
    2.5. 室外的文本识别（Text (in the Wild) Recognition）
    2.6. 脑机接口（Brain Computer Interfacing）
    2.7. 自动驾驶汽车（Self-Driving Cars）
    2.8. 目标识别（Object Recognition）
    2.9. 标识识别（Logo Recognition）
    2.10. 超分辨率（Super Resolution）
    2.11. 姿态估计（Pose Estimation）
    2.12. 图像描述（Image Captioning）
    2.13. 图像压缩（Image Compression）
    2.14. 图像合成（Image Synthesis）
    2.15. 面部识别（Face Recognition）
3. 音频
    3.1. 音频合成（Audio Synthesis）
4. 其它
    4.1. 未分类
    4.2. 正则化（Regularization）
    4.3. 神经网络压缩（Neural Network Compression）
    4.4. 优化器（Optimizers）

 

 

顶级会议的重要性

我在机器学习、计算机视觉和人工智能领域，顶级会议才是王道。顶级会议的重要性无论怎么强调都不为过。

可以从以下几点说明：

（1）因为机器学习、计算机视觉和人工智能领域发展非常迅速，新的工作层出不穷，如果把论文投到期刊上，一两年后刊出时就有点out了。因此大部分最新的工作都首先发表在顶级会议上，这些顶级会议完全能反映“热门研究方向”、“最新方法”。

（2）很多经典工作大家可能引的是某顶级期刊上的论文，这是因为期刊论文表述得比较完整、实验充分。但实际上很多都是在顶级会议上首发。比如PLSA, Latent Dirichlet Allocation等。

（3）如果注意这些领域大牛的pulications，不难发现他们很非常看重这些顶级会议，很多人是80%的会议+20%的期刊。即然大牛们把最新工作发在顶级会议上，有什么理由不去读顶级会议？

(1)
以下是不完整的列表，但基本覆盖。
机器学习顶级会议：　　NIPS, ICML, UAI, AISTATS;  （期刊：JMLR, ML, Trends in ML, IEEE T-NN）
计算机视觉和图像识别：ICCV, CVPR, ECCV;  （期刊：IEEE T-PAMI, IJCV, IEEE T-IP）
人工智能：　　　　　　IJCAI, AAAI; （期刊AI）

另外相关的还有SIGRAPH, KDD, ACL, SIGIR, WWW等。

神经信息处理系统大会 (Conference and Workshop on Neural Information Processing Systems)

国际机器学习大会 (International Conference on Machine Learning)

特别是，

• • 如果做机器学习，必须地，把近4年的NIPS, ICML翻几遍；
  • 如果做计算机视觉，要把近4年的ICCV, CVPR, NIPS, ICML翻几遍。

(2)
另外补充一下：大部分顶级会议的论文都能从网上免费下载到，比如

CV方面：http://www.cvpapers.com/index.html; 

NIPS: http://books.nips.cc/;  

JMLR(期刊): http://jmlr.csail.mit.edu/papers/;  

COLT和ICML(每年度的官网): http://www.cs.mcgill.ca/~colt2009/proceedings.html。

希望这些信息对大家有点帮助。

 

(3)
说些自己的感受。我的研究方向主要是统计学习和概率图模型，但对计算机视觉和计算神经科学都有涉及，对Data mining和IR也有些了解。

这些领域，从方法和模型的角度看，统计模型（包括probabilistic graphical model和statistical learning theory）是主流也是非常有影响力的方法。

有个非常明显的趋势：

1. 1. 重要的方法和模型最先在NIPS或ICML出现，
   2. 然后应用到CV, IR和 MM。

虽然具体问题和应用也很重要，但多关注和结合这些方法也很有意义。