[Algorithm] Sort for Fun!

Updated, July, 2019

---

2011年的原文

看到园子里有人发排序算法的随笔，想起之前发现的一个好网页，日本人写的，用脚本编写的一个算法柱形图演示，很是形象。趁着一时的兴趣，也就自己写了个程序，希望能通过终端实现类似的演示效果。写了一半，最后的图形显示遇到点小麻烦，之后也就忙的没再解决。

程序也简单，将不同的算法模块加进去，比较不同的算法的排序效率。当一百万的随机数用快排在数秒钟搞定，而其他则是花费数倍，甚至十几倍的时间才能出结果时，“效率”两个字便突然间有了很重要的地位。花时间在代码质量方面做做文章，虽不会有立竿见影的效果，但对一个人的编程态度会有很大的改观。米卢不是说了么：“态度决定一切”。

这个是日本人的那个网页链接：http://jsdo.it/norahiko/oxIy/fullscreen

 

 

OUTLINE

Ref: 十大经典排序算法最强总结

 

 

一、比较排序法

选择排序：关键是　再剩余项中选出最大值。

冒泡排序：关键是　两个循环，与“选择排序”相比，会有频繁的“相邻的两两比较”。

插入排序：list preferred，讲剩余项中选出一个插入到“已有序的序列”中。

 

希尔排序：

希尔排序也是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序，同时该算法是冲破O(n2）的第一批算法之一。

－　通过排序子列表， 我们已将项目移动到更接近他们实际所属的位置。

－　最后一次就是增量为１的标准插入排序，但此时大部分是有序的。

－　通过执行之前的子列表排序， 我们减少了将列表置于其最终顺序所需的移位操作的总数。

[与插入排序的不同之处]

它会优先比较距离较远的元素。希尔排序又叫缩小增量排序 (“希尔增量”是减半变化的，但不是最优的选择)。

 

快速排序：（Quick Sort）

快排之所以块，就是因为它高度优化的内部循环（分割）。

它既不像 "归并排序" 那样需要辅助数组来回复制元素，也不像 "堆排序" 无法利用缓存并且有许多无用的比较，并且最坏情况可以采用一些方法避免。

 

• 最左边的6作为“基准”，右边先走，“不对劲”时轮到左边走。（同时走也是可以的）

 

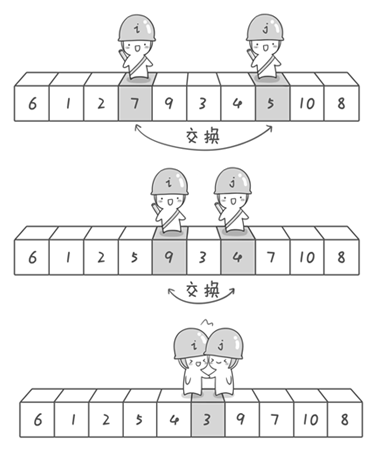
• 交换6和3，3作为下一次的“基准”。此时，6的左边都小于6，6的右边都大于6。

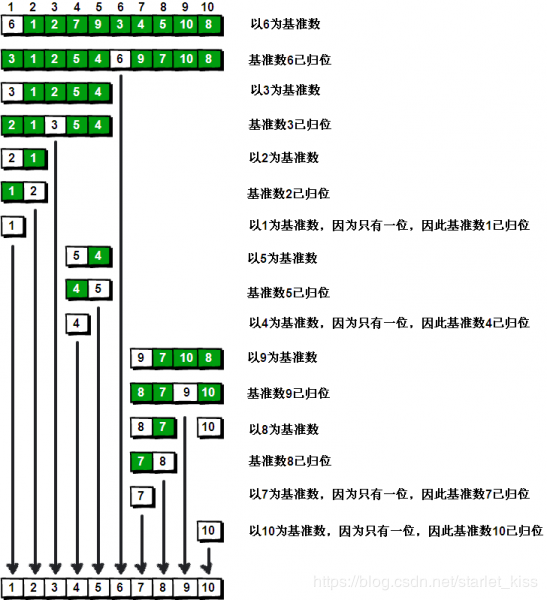
#include<stdio.h>

void Swap(int arr[], int low, int high)
{
    int temp;
    temp = arr[low];
    arr[low] = arr[high];
    arr[high] = temp;
}

//////////////////////////////////////////////////////

int Partition(int arr[], int low, int high)
{
    int base = arr[low];
    while(low < high)
    {
        while(low < high && arr[high] >= base)
        {
            high --;
        }
        Swap(arr, low, high);
        while(low < high && arr[low] <= base)
        {
            low ++;
        }
        Swap(arr, low, high);
    }
    return low;
}

//////////////////////////////////////////////////////

void QuickSort(int arr[], int low, int high)
{
    if(low < high)
    {
        int base = Partition(arr, low, high);　　// 可随机选择主元
        QuickSort(arr, low, base - 1);
        QuickSort(arr, base + 1, high);
    }
}

//////////////////////////////////////////////////////

int main()
{
    int n;
    scanf("%d\n",&n);
    int arr[n];
    int i , j;
    for(i = 0; i < n; i ++)
    {
        scanf("%d",&arr[i]);
    }
    printf("\n");
    QuickSort(arr, 0, n-1);
    for(j = 0; j < n; j ++)
    {
        printf("%4d",arr[j]);
    }
    return 0;
}

 

归并排序：（Merge Sort）也可适用于“外存”；但频繁复制降低了效率。

def mergeSort(alist):
　　print("Splitting ",alist)
　　if len(alist)>1:
　　　　mid = len(alist)//2
　　　　lefthalf = alist[:mid]
　　　　righthalf = alist[mid:]

　　　　mergeSort(lefthalf)
　　　　mergeSort(righthalf)

　　　　i=0
　　　　j=0
　　　　k=0
　　　　# 俩指针同步移动
　　　　while i < len(lefthalf) and j < len(righthalf):
　　　　　　if lefthalf[i] < righthalf[j]:
　　　　　　　　alist[k]=lefthalf[i]
　　　　　　　　i=i+1
　　　　　　else:
　　　　　　　　alist[k]=righthalf[j]
　　　　　　　　j=j+1
　　　　　　k=k+1

　　　　# 剩余部分的处理
　　　　while i < len(lefthalf):
　　　　　　alist[k]=lefthalf[i]
　　　　　　i=i+1
　　　　　　k=k+1

　　　　while j < len(righthalf):
　　　　　　alist[k]=righthalf[j]
　　　　　　j=j+1
　　　　　　k=k+1

　　print("Merging ",alist)


alist = [54,26,93,17,77,31,44,55,20]
mergeSort(alist)
print(alist)

 

堆排序：（Heap Sort）每次更新都需维护，无法充分利用缓冲技术。

  

Tim排序：Python、 Java、 Android平台 和 GNU Octave 的默认排序算法。 

Ref: Timsort——自适应、稳定、高效排序算法

针对现实中需要排序的数据分析看，大多数据通常是有部分已经排好序的数据块，Timsort 就利用了这一特点。

本质上 Timsort 是一个经过大量优化的归并排序，而归并排序已经到达了最坏情况下，比较排序算法时间复杂度的下界，所以在最坏的情况下，Timsort 时间复杂度为 O(nlogn)O(nlogn)O(nlogn)。在最佳情况下，即输入已经排好序，它则以线性时间运行O(n)O(n)O(n)。可以看出Timsort是目前最好的排序方式。

Ref: Tim Sort Explained

(1) Binary Insertion Sort.

窗口逐渐增大，所以新的元素要插入“sorted"的序列时，可以通过二分查找法找到插入位置。

(2) Chunk

Chunk，也可能叫做"run"：从左到右，如下，当发现有一个元素不是”递增“ or ”递减“时，插入排序，然后当chunk结束；

遍历整个序列后，便得到一堆的”有序小序列”。（有点希尔排序的意思）

(3) Merging runs efficiently

不等长序列的合并，如何高效实现。

[优化一]

涉及到贪心算法，序列长度排序，从小的开始两两合并。

如此，有点Fibonacci的意思：Run(n) > Run(n-1) + Run(n-2)

(4) Merging runs optimally with Galloping

[优化二] 

合并过程中，需要找到合适的点，这是一个搜索问题，可以考虑"Galloping research"。

 

From: TimSort | Sorting Algorithm【代码】

import random

def InsertionSort(array):

    for x in range (1, len(array)):
        for i in range(x, 0, -1):
            if array[i] < array[i - 1]:
                t = array[i]
                array[i] = array[i - 1]
                array[i - 1] = t
            else:
                break
            i = i - 1
    return array

def Merge(aArr, bArr):
    
    a = 0
    b = 0
    cArr = []

    while a < len(aArr) and b < len(bArr):
        if aArr[a] < bArr[b]:
            cArr.append(aArr[a])
            a = a + 1
        elif aArr[a] > bArr[b]:
            cArr.append(bArr[b])
            b = b + 1
        else:
            cArr.append(aArr[a])
            cArr.append(bArr[b])
            a = a + 1
            b = b + 1

    while a < len(aArr):
        cArr.append(aArr[a])
        a = a + 1

    while b < len(bArr):
        cArr.append(bArr[b])
        b = b + 1

    return cArr

def TimSort():

    for x in range(0, len(arr), RUN):
        arr[x : x + RUN] = InsertionSort(arr[x : x + RUN])
    RUNinc = RUN
    while RUNinc < len(arr):
        for x in range(0, len(arr), 2 * RUNinc):
            arr[x : x + 2 * RUNinc] = Merge(arr[x : x + RUNinc], arr[x + RUNinc: x + 2 * RUNinc])
        RUNinc = RUNinc * 2


arr = []
RUN = 32
for x in range(0, 50):
    arr.append(random.randint(0, 100))
TimSort()
print(arr)

 

 

二、非比较排序法

桶排序是基础

Ref: 基数排序、桶排序和计数排序的区别

其中, d 表示位数， k 在基数排序中表示 k 进制，在桶排序中表示桶的个数， maxV 和 minV 表示元素最大值和最小值。

首先，基数排序和计数排序都可以看作是桶排序。

• • 计数排序本质上是一种特殊的桶排序，当桶的个数取最大( maxV-minV+1 )的时候，就变成了计数排序。
  • 基数排序也是一种桶排序。桶排序是按值区间划分桶，基数排序是按数位来划分；基数排序可以看做是多轮桶排序，每个数位上都进行一轮桶排序。

 

基数排序"退化"

当用最大值作为基数时，基数排序 ----> 退化成 ----> 计数排序。

当使用2进制时， k=2 最小，位数 d 最大，时间复杂度 O(nd) 会变大，空间复杂度 O(n+k) 会变小。

当用最大值作为基数时， k=maxV 最大， d=1 最小，此时时间复杂度 O(nd) 变小，但是空间复杂度 O(n+k) 会急剧增大，此时基数排序退化成了计数排序。
 

 

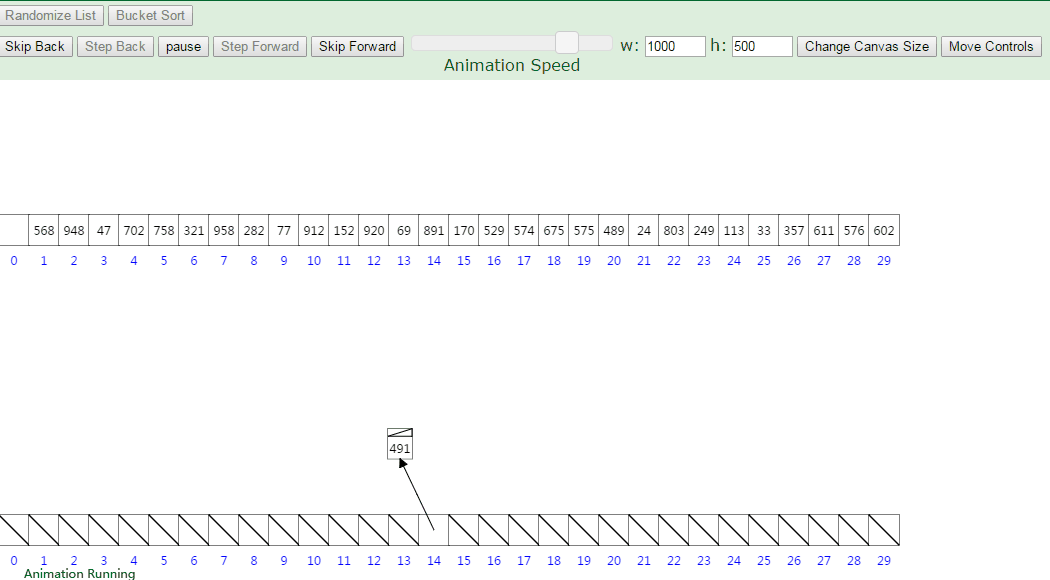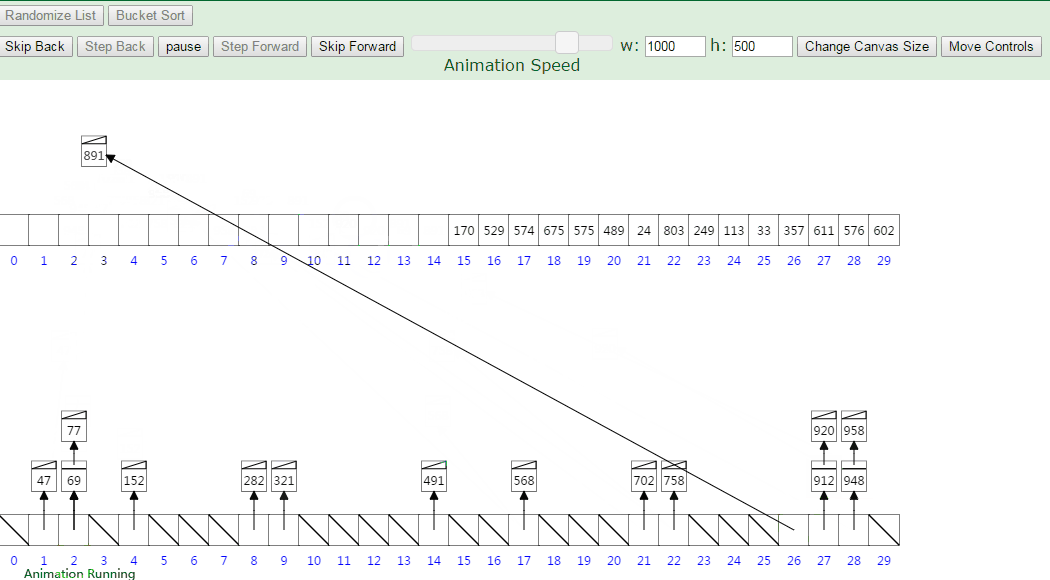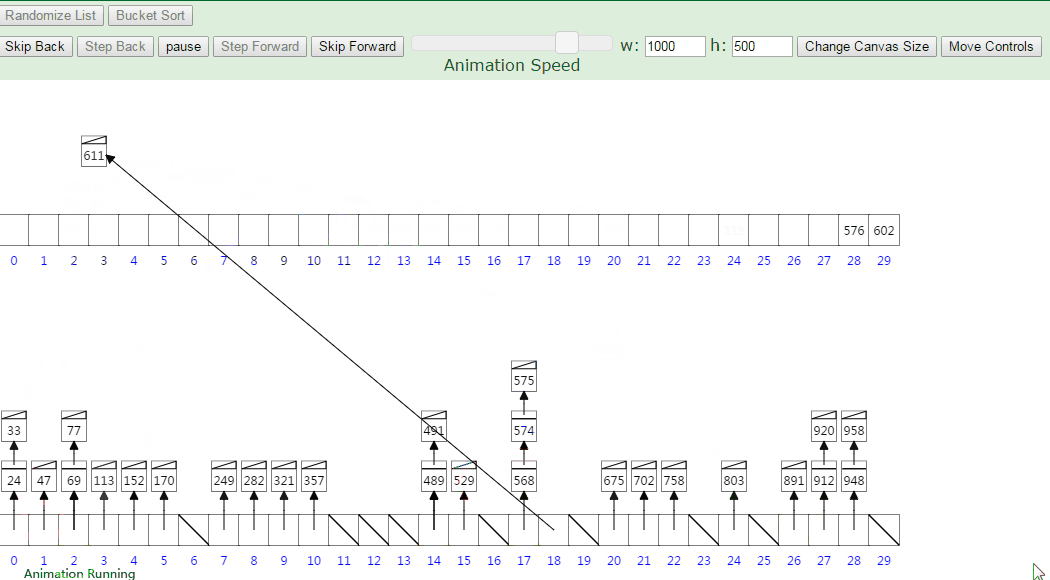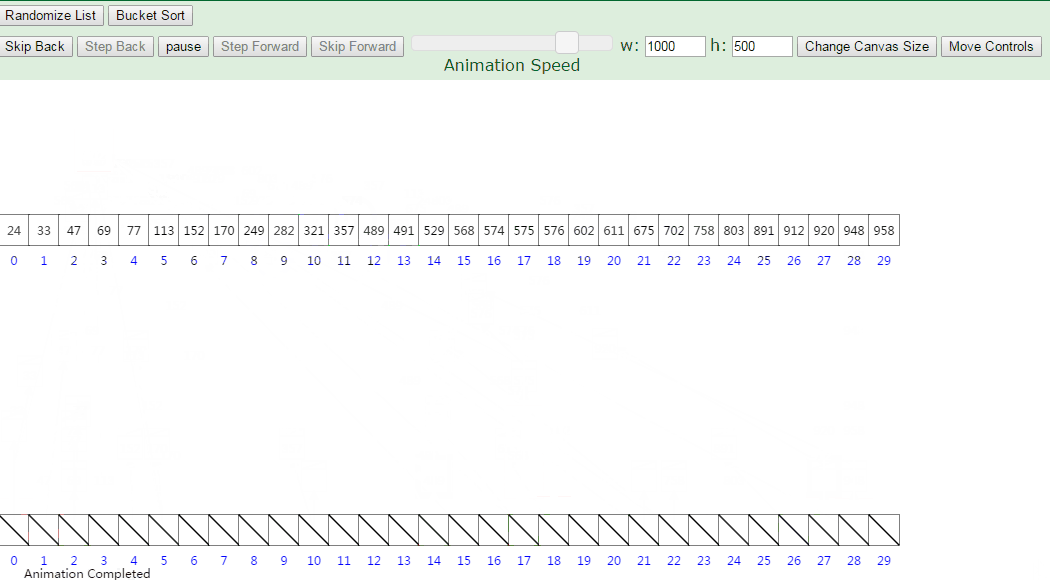
桶排序：（Bucket Sort）

Ref: 算法：排序算法之桶排序

利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。

 

基数排序：（Radix Sort）

Ref: 基数排序 顺序实现与链式实现

 

计数排序：（Counting Sort）

Ref: 漫画：什么是计数排序？ 

以“数列最大值和最小值的差+1”作为统计数组的长度。

 

 

三、大数据排序

Ref: 硅谷之路 054 深入浅出Spark（七）如何排序100TB Preview

/* 略，不在此学习，但仍然是一个不可忽视的话题 */

 

  

2011年的旧代码

下面是我的这个小程序，随便一看。

#ifndef _HEAD_H_
#define _HEAD_H_

#include<stdio.h>
#include<stdlib.h>
#include<string.h>

#include <unistd.h>
#include <sys/times.h>

#define FOR(i, count)   \
    for(i = 0; i < count; ++i)

#endif
#include"head.h"

#define COUNT   1000000     //比较的数字个数，randArr[0]有其他用处。
#define LEN     (COUNT+1)
#define ROW     
#define COL     (COUNT+1)
#define TIME_VALUE  200000    //改速度



#define BLACK       40
#define WHITE       47
#define RED         41
#define PURPLE      45
#define GREEN       42
#define BLUE        44


#define BG  BLACK
#define FG  WHITE 



int randArr[COUNT+1];    //randArr[0]有其他用处。
int dlta[] = {5, 3, 1};

typedef enum {
    StraightInsertion = 0,
    Shell = 1,
    Quick = 2,
    Merge = 3,
    Bubble = 4,
    Heap = 5,
    /*添加算法标志*/
}SORTING_STYPE;

//------------------------------------------------------------------------

typedef int* TYPE;  

int swap(TYPE a, TYPE b)
{
    *a ^= *b; 
    *b ^= *a; 
    *a ^= *b; 

    return 0;
}





//------------------------------------------------------------------------

void _draw_clr(int which)    //which: 把第几个柱子清除
{
    int i, j;

    /*draw column*/
    FOR(j, ROW) {

        printf("\33[%d;%dH", j, which);
        printf("\33[%dm \33[0m", BG);
    }  
    printf("\33[%d;%dH", ROW, which);
}


void _draw_col(int which, int color )    //以何种颜色显示第几根柱子
{
    int i, j;

    /*clear column*/
    _draw_clr(which);

    /*draw column*/
    FOR(j, randArr[which]) {

        printf("\33[%d;%dH", j, which);
        printf("\33[%dm \33[0m", color);
    }  
    printf("\33[%d;%dH", ROW, which);
    usleep(TIME_VALUE);
}

//------------------------------------------------------------------------


void drawArr(void)
{
    int i, j;

#if 0
    /*clear and init tty*/
    printf("\33[1;1H");

    FOR(i, ROW) {
        FOR(j, COL) {

            printf("\33[%dm \33[0m", BG);
        }   
        printf("\n");
    }

    FOR(i, LEN) {
        FOR(j, randArr[i]) {
            printf("\33[%d;%dH", j, i+1);
            printf("\33[%dm \33[0m", FG);
        }
    }

    printf("\33[%d;%dH", ROW-2, 0);

#endif

#if 1
    FOR(j, COUNT) {
        printf("randArr[%d] = %d\n", j+1, randArr[j+1]);
    }
#endif
}


void init(void)
{
    int i = 0, j = 0;
    srand(getpid());

    /*80 number*/
    FOR(i, COUNT) {
        randArr[i+1] = rand() % ROW + 1;
        //randArr[i+1] = i;
    }

    //drawArr();
}

//------------------------------------------------------------------------

/*排序参数简化，查找参数要全*/

/*查找*/

int Search_Bin(int low, int high, int key)
{
    int mid = 0;

    while (low < high)
    {
        mid = (low + high) >> 1;
        if (randArr[mid] == key)
        {
            return mid;
        }
        else if (randArr[mid] > key) 
        {
            high = mid - 1;
        }
        else 
        {
            low = mid + 1;
        }
    }
    
    return 0;
}


//------------------------------------------------

/*排序算法实现*/
/*排序的图形化演示，未实现，有兴趣可以一试*/
/*
void InsertSort(void)
{
    int i = 0, j = 0;

    for (i = 2; i <= COUNT; ++i)
    {
_draw_col(i, RED);
_draw_col(i-1, GREEN);
        if(randArr[i] < randArr[i-1])   //not ascend...
        {
_draw_col(i-1, FG);
//_draw_col(i-1, BLUE);

_draw_clr(i);
            randArr[0] = randArr[i];
_draw_col(0, RED);

_draw_clr(i-1);
            randArr[i] = randArr[i-1];
_draw_col(i, GREEN);
_draw_col(i, FG);

            j = i - 1;
_draw_col(0, RED);
_draw_col(j, GREEN);
            while(randArr[0] < randArr[j])
            {
//_draw_col(0, BLUE);

_draw_clr(j);
                randArr[j+1] = randArr[j];
_draw_col(j+1, GREEN);
_draw_col(i, FG);
                --j;
_draw_col(0, RED);
_draw_col(j, GREEN);
            }
_draw_col(j, FG);
_draw_clr(0);
            randArr[j+1] = randArr[0];
_draw_col(j+1, RED);

        }
_draw_col(i, FG);
_draw_col(i-1, FG);
    }
}
*/


void InsertSort(void)
{
    int i = 0, j = 0;
    int tmp = 0;
    
    for (i = 2; i <= COUNT; ++i)
    {
        if(randArr[i] < randArr[i-1]) 
        {
            /*放哨兵*/
            randArr[0] = randArr[i];
            
            /*找位置*/
            j = i - 2;
            while(randArr[0] < randArr[j])
            {
                --j;
            }
            
            /*整体移动，腾位置*/
            tmp = i-1;
            while(j+1 <= tmp)
            {
                randArr[tmp+1] = randArr[tmp];
                --tmp;
            }

            /*坐位置*/
            randArr[j+1] = randArr[0];
        }
    }
}

//--------------------------------------------

void ShellInsert(int dk)
{
    int i = 0, j = 0;
    int tmp = 0;

    for (i = dk+1; i <= COUNT; ++i)
    {   
        if(randArr[i] < randArr[i-1*dk]) 
        {
            /*放哨兵*/
            randArr[0] = randArr[i];
            
            /*找位置*/
            j = i - 2*dk;
            while(randArr[0] < randArr[j])
            {
                j -= dk;
            }
            
            /*整体移动，腾位置*/
            tmp = i - 1*dk;
            while(j+1*dk <= tmp)
            {
                randArr[tmp+1*dk] = randArr[tmp];
                tmp -= dk;
            }

            /*坐位置*/
            randArr[j+1*dk] = randArr[0];
        }
    }
}


void ShellSort(void)
{
    int k = 0;
    int t = 3;
    int shellArr[] = {5, 3, 1};
    
    //按增量序列dlta[0..t-1]对顺序表作排序
    for (k = 0; k < t; ++k)
    {
        ShellInsert(shellArr[k]);
    }
}



//------------------------------------------------------------------------

int Partition2(int low, int high)   //升级版， 取中值
{
    int tmp = 0;        //= randArr[low];
    int pivotkey = 0;   //= randArr[low];
    int mid = 0;

    mid = (low + high) / 2;
    swap(&randArr[mid], &randArr[low]);
    
    tmp = randArr[low];
    pivotkey = randArr[low];

    while(low < high)
    {
        while(low < high && randArr[high] >= pivotkey)
        {
            --high;
        }
        randArr[low] = randArr[high];

        while(low < high && randArr[low] <= pivotkey)
        {
            ++low;
        }
        randArr[high] = randArr[low];
    }
    
    randArr[low] = tmp;

    return low;
}

int Partition(int low, int high)
{
    int tmp = randArr[low];
    int pivotkey = randArr[low];

    while(low < high)
    {
        while(low < high && randArr[high] >= pivotkey)
        {
            --high;
        }
        randArr[low] = randArr[high];

        while(low < high && randArr[low] <= pivotkey)
        {
            ++low;
        }
        randArr[high] = randArr[low];
    }
    
    randArr[low] = tmp;

    return low;
}



void QSort(int low, int high)
{
    int pivotloc;

    if (low < high)
    {
        pivotloc = Partition2(low, high);
        QSort(low, pivotloc-1);
        QSort(pivotloc+1, high);
    }
}


void QuickSort2(void)
{
    QSort(1, COUNT);
}


void QuickSort(void)
{
    QSort(1, COUNT);
}


//------------------------------------------------------------------------


void merge(int tmpArr[], int i, int m, int n)
{
    int j = m + 1;
    int k = i;

    while(i <= m && j <= n)
    {
        if (randArr[i] < randArr[j])
        {
            tmpArr[k++] = randArr[i++];
        }
        else
        {
            tmpArr[k++] = randArr[j++];
        }
    }

    while (i <= m)
    {
        tmpArr[k++] = randArr[i++];
    }
    while (j <= n)
    {
        tmpArr[k++] = randArr[j++];
    }
}



void copy(int mergeArr[], int l, int r)
{
    int i;
    for( i = l ; i <= r; i ++ ){
        randArr[i] = mergeArr[i];
    }
}



void Msort(int mergeArr[], int left, int right)
{
    int mid;

    if( left < right )
    {
        mid = ( left + right ) / 2;
        Msort(mergeArr, left, mid );    
        Msort(mergeArr, mid + 1, right );

        merge (mergeArr, left, mid, right );
        copy(mergeArr, left, right );
    }   
}



void MergeSort()
{
    int randArrMerge[COUNT+1];

    Msort(randArrMerge, 1, COUNT);
}





//------------------------------------------------------------------------

void BubbleSort(void)
{
    int i, j;
    FOR(i, COUNT-1) {
        FOR(j, COUNT - 1 - i) {

            swap(&randArr[j], &randArr[j+1]);
        }
    }
}

//------------------------------------------------------------------------


/* i为根节点,n为节点总数...关键 */
void sift(int a[], int i, int n)
{
    int child, tmpParent;

    for (tmpParent = a[i]; n >= 2 * i; i = child)
    {
        /* i的左孩子为2*i,右孩子为2*i+1 */
        child = 2 * i;

        /* 让child指向孩子中较大的一个 */
        if (child != n && a[child + 1] > a[child])
        {   
            /*i*2之后且=n，表明为左孩子即当前末结点*/
            
            child++;
        }

        /* 如果孩子节点大 */
        if (tmpParent < a[child])
        {
            /* 交换孩子节点和根节点 */
            a[i] = a[child];
        }
        else 
        {
            /*若比孩子结点大，肯定比孙子大，则不用再比较*/
            break;
        }
    }

    /* 将根放在合适位置, tmpParent无需每次移动 */
    a[i] = tmpParent;
}



void heapsort(int a[], int n)
{
    int i;

    /* 将a[1...n]建成大根堆 */
    for (i = n / 2; i >= 1; i--)
    {
        sift(a, i, n);
    }


    /* 进行n-1趟排序 */
    for (i = n; i >= 2; i--)
    {
        /* 交换堆顶元素和最后一个元素 */
        swap(&a[1], &a[i]);

        /* 将a[1...i-1]重建为大顶堆 */
        sift(a, 1, i-1);
    }
} 



void HeapSort(void)
{
    heapsort(randArr, COUNT);
}


//------------------------------------------------------------------------


void do_job(int style)
{

    switch(style) {
        case StraightInsertion:
            {
                fprintf(stderr, "\nStraight Insertion Sort:\n");
                InsertSort();
                break;
            }
        case Shell:
            {
                fprintf(stderr, "\nShell's Sort:\n");
                ShellSort();
                break;
            }
        case Quick:
            {
                fprintf(stderr, "\nQuick Sort:\n");
                QuickSort();
                break;
            }
        case Merge: //超过一百万 堆栈溢出
            {
                fprintf(stderr, "\nMerge Sort:\n");
                MergeSort();
                break;
            }
         case Bubble:
            {
                fprintf(stderr, "\nBubble Sort:\n");
                BubbleSort();
                break;
            }
          case Heap:
            {
                fprintf(stderr, "\nHeap Sort:\n");
                HeapSort();
                break;
            }
            /*这里添加排序算法*/

        default:
            {
                break;
            }
    }
}

//------------------------------------------------------------------------

int main(void)
{

    clock_t start, end;

 

End.