hdu 5093 Battle ships （二分图）

二分图最大匹配问题

遇到冰山就把行列拆成两个部分。每个部分x也好，y也好只能匹配一次

图画得比较草，将就着看

 

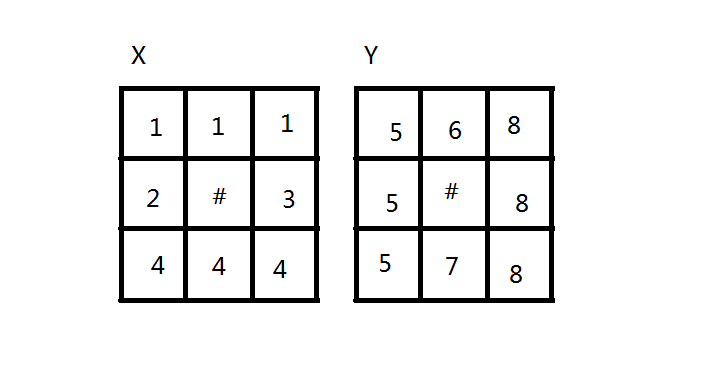
横着扫一遍，竖着扫一遍，得到编号

一个位置就对应一个（xi，yi）就是X集到Y集的一条边，

由题意，每个点只能被选择一次。所以最大匹配的边数就是答案了。

 

算法过程

当增广路不存在的时候，就是二分图最大匹配。（同样适用其他任意图，可以求最大流）

通常都是先贪心求一个匹配，然后开始增广。

寻找增广路的过程：

　　一个没有和任意边匹配的点叫做未盖点，从左集X中一个未盖点u出发寻找增广路。

　　从u出发，选一个非匹配边到达Y集中的v，如果v没匹配，那么就找到一条增广路（只要把之前走过的匹配边和非匹配边交换，匹配边数加一）。否则沿着v的匹配边回来，然后重复以上过程。

做这题的过程中，把数组开小了导致TLE...还加了个反向边，不过在debug过程中到是发现了不用每次都memset vis数组的小技巧

#include<cstdio>
#include<cstring>

const int maxn = 52;
const int maxv = 2550; // 500
const int maxe = (maxv*maxv);
char pg[maxn][maxn];
int g[maxn][maxn][2];

int to[maxe],nxt[maxe],head[maxv],ecnt;
int match[maxv];


void addEdge(int u,int v)
{
    to[ecnt] = v;
    nxt[ecnt] = head[u];
    head[u] = ecnt++;
}

int vis[maxv];
int times;
//find augmenting path
bool dfs(int u)
{
    for(int i = head[u]; ~i; i = nxt[i]){
        int v = to[i];
        if(vis[v]!= times){
            vis[v]  = times;
            if(!~match[v] || dfs(match[v]) ){
                match[v] = u;
                return true;
            }
        }

    }
    return false;
}

int x_num,y_num;

void go()
{
    memset(match,-1,sizeof(match));
    int ans = 0;
    for(int i = 0; i < x_num; i++ ){
        times++;
        if(dfs(i)) ans++;
    }
    printf("%d\n",ans);
}

void init(){
    memset(head,-1,sizeof(head));
    ecnt = 0;
    x_num = 0;
}
int main()
{
    //freopen("in.txt","r",stdin);
    int T;
    times = 0;
    scanf("%d",&T);
    while(T--){
        init();
        int m,n;
        scanf("%d%d",&m,&n);
        for(int i = 0; i < m; i++)
            scanf("%s",pg[i]);
        bool flag;//如果某行没有找到那么编号不应该增加
        for(int i = 0; i < m; i++){
            flag = false;
            for(int j = 0; j < n; j++){
                if(pg[i][j] == 'o') g[i][j][0] = -1;
                else if(pg[i][j] == '#') g[i][j][0] = -1,x_num++;
                else g[i][j][0] =  x_num,flag = true;
            }
            if(flag) x_num++;
        }

        y_num = x_num;
        for(int j = 0; j < n; j++){
            flag = false;
            for(int i = 0; i < m; i++){
                 if(pg[i][j] == 'o') ;
                else if(pg[i][j] == '#') y_num++;
                else g[i][j][1] =  y_num,flag = true;
            }
            if(flag) y_num++;
        }

        for(int i = 0; i < m; i++)
            for(int j = 0; j < n; j++){
                if(~g[i][j][0]){
                    addEdge(g[i][j][0],g[i][j][1]);
                }
            }
        go();
    }
    return 0;
}