拓扑排序
拓扑排序
一、概述
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若<u,v> ∈E(G),则u在线性序列中出现在v之前。
通常,这样的线性序列称为满足拓扑次序(TopoiSicai Order)的序列,简称拓扑序列。
注意:
①若将图中顶点按拓扑次序排成一行,则图中所有的有向边均是从左指向右的。
②若图中存在有向环,则不可能使顶点满足拓扑次序。
③一个DAG的拓扑序列通常表示某种方案切实可行。
【例】一本书的作者将书本中的各章节学习作为顶点,各章节的先学后修关系作为边,构成一个有向图。按有向图的拓扑次序安排章节,才能保证读者在学习某章节时,其预备知识已在前面的章节里介绍过。
④一个DAG可能有多个拓扑序列。
【例】对图G9进行拓扑排序,至少可得到如下的两个(实际远不止两个)拓扑序列:C0,C1,C2,C4,C3,C5,C7,C8,C6和C0,C7,C9,C1,C4,C2,C3,C6,C5。
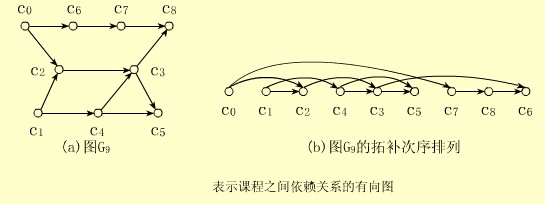
⑤当有向图中存在有向环时,拓扑序列不存在
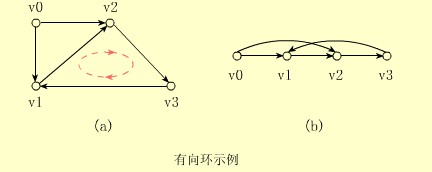
【例】下面(a)图中的有向环重排后如(b)所示,有向边<v3,vl>和其它边反向。若有向图被用来表示某项工程实施方案或某项工作计划,则找不到该图的拓扑序列(即含有向环),就意味着该方案或计划是不可行的。
二、无前趋的顶点优先的拓扑排序方法
该方法的每一步总是输出当前无前趋(即人度为零)的顶点,其抽象算法可描述为:
NonPreFirstTopSort(G){//优先输出无前趋的顶点
while(G中有人度为0的顶点)do{
从G中选择一个人度为0的顶点v且输出之;
从G中删去v及其所有出边;
}
if(输出的顶点数目<|V(G)|)
//若此条件不成立,则表示所有顶点均已输出,排序成功。
Error("G中存在有向环,排序失败!");
}
注意:
无前趋的顶点优先的拓扑排序算法在具体存储结构下,为便于考察每个顶点的人度,可保存各顶点当前的人度。为避免每次选入度为0的顶点时扫描整个存储空间,可设一个栈或队列暂存所有入度为零的顶点:
在开始排序前,扫描对应的存储空间,将人度为零的顶点均入栈(队)。以后每次选人度为零的顶点时,只需做出栈(队)操作即可。
三、无后继的顶点优先拓扑排序方法
1、思想方法
该方法的每一步均是输出当前无后继(即出度为0)的顶点。对于一个DAG,按此方法输出的序列是逆拓扑次序。因此设置一个栈(或向量)T来保存输出的顶点序列,即可得到拓扑序列。若T是栈,则每当输出顶点时,只需做人栈操作,排序完成时将栈中顶点依次出栈即可得拓扑序列。若T是向量,则将输出的顶点从T[n-1]开始依次从后往前存放,即可保证T中存储的顶点是拓扑序列。
2、抽象算法描述
算法的抽象描述为:
NonSuccFirstTopSort(G){//优先输出无后继的顶点
while(G中有出度为0的顶点)do {
从G中选一出度为0的顶点v且输出v;
从G中删去v及v的所有人边
}
if(输出的顶点数目<|V(G)|)
Error("G中存在有向环,排序失败!");
}
3、算法求精
在对该算法求精时,可用逆邻接表作为G的存储结构。设置一个向量outdegree[0..n-1]或在逆邻接表的顶点表结点中增加1个出度域来保存各顶点当前的出度;设置一个栈或队列来暂存所有出度为零的顶点。除了增加一个栈或向量T来保存输出的顶点序列外,该算法完全类似于NonPreFirstTopSort。
四、利用深度优先遍历对DAG拓扑排序
当从某顶点v出发的DFS搜索完成时,v的所有后继必定均已被访问过(想像它们均已被删除),此时的v相当于是无后继的顶点,因此在DFS算法返回之前输出顶点v即可得到 DAG的逆拓扑序列。
其中第一个输出的顶点必是无后继(出度为0)的顶点,它应是拓扑序列的最后一个顶点。若希望得到的不是逆拓扑序列,同样可增加T来保存输出的顶点。若假设T是栈,并在DFSTraverse算法的开始处将T初始化,
利用DFS求拓扑序列的抽象算法可描述为:
1 void DFSTopSort(G,i,T) 2 { 3 //在DisTraverse中调用此算法,i是搜索的出发点,T是栈 4 int j; 5 visited[i]=TRUE; //访问i 6 for(所有i的邻接点j)//即<i,j>∈E(G) 7 if(!visited[j]) 8 DFSTopSort(G,j,T); 9 //以上语句完全类似于DFS算法 10 Push(&T,i); //从i出发的搜索已完成,输出i 11 }
只要将深度优先遍历算法DFSTraverse中对DFS的调用改为对DFSTopSort的调用,即可求得拓扑序列T。其具体算法不难从上述抽象算法求精后得到。
若G是一个DAG,则用DFS遍历实现的拓扑排序与NonSuccFirstTopSort算法完全类似;但若C中存在有向环,则前者不能正常工作。
*************************************************************************
dfs实现拓扑排序 函数(算法竞赛入门经典)
1 E(u,v) 2 3 4 5 int c[maxn]; 6 7 int topo[maxn],t; 8 9 bool dfs(int u) 10 11 { 12 13 c[u]=-1; //开始访问该顶点 14 15 for(int v=0;v<n;v++) 16 17 { 18 19 if(G[u][v]==1) 20 21 { 22 23 if(c[v]<0) return false; //c[v]=-1代表正在访问该定点(即递归调用dfs(u)正在帧栈中,尚未返回) 24 25 else if(!c[v] && !dfs(v)) return false; //(c[v]==0 && dfs(v)==false即当前顶点没有后即顶点时, 26 27 //开始返回 (结束)) 28 29 } 30 31 } 32 33 c[u]=1; //访问结束 34 35 topo[--t]=u; 36 37 return true; 38 39 } 40 41 42 43 bool toposort() 44 45 { 46 47 t=n; 48 49 memset(c,0,sizeof(c)); 50 51 for(int u=0;u<n;u++) 52 53 if(!c[u]) if(!dfs()) return false; 54 55 return ture; 56 57 }
1 int graph[narray][narray]; //邻接阵 2 int indegree[narray]; //记录顶点的入度 3 int n; //n为顶点个数 4 memset(graph,0,sizeof(graph)); 5 memset(indegree,0,sizeof(indegree)); 6 for(i=1;i<=n;++i) //遍历n次每次找出一个顶点 7 { 8 for(j=1;j<=n;++j) //遍历所有的结点 9 { 10 if(indegree[j]==0) 11 { 12 indegree[j]--; //该顶点的入度为-1,防止该顶点被在此遍历到 13 if(i!=n) printf("%d ",j); 14 else printf("%d\n",j); 15 for(k=1;k<=n;++k) 16 { 17 if(graph[j][k]) 18 indegree[k]--; //与该顶点关联的顶点的入度递减 19 } 20 break; 21 } 22 } 23 }



