斯坦福机器学习实现与分析之三（逻辑回归）

　　前一节讲线性回归已提过，回归问题的根本目的在于预测。直观上看，线性回归训练与预测的值域都为实数域R，而逻辑回归训练样本值域为{0,1}，预测的值域则是(0,1)，也就是说逻辑回归用于分类，其结果能给出样本属于某个类的概率。逻辑回归逻辑回归作为机器学习中的一个简单而有效的算法，其应用之广泛已超出我们的想象。

 

逻辑回归算法推导

---

　　首先，确定逻辑回归函数模型，如下：

\(\begin{aligned} h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}} \end{aligned}\)

　　可以看出该函数定义域为实数域R，值域为(0,1)。这里关于选择该函数的原因暂不讨论，待后面广义线性模型一节再讲。先看看该函数的一个特性，令

\(\begin{aligned} g(z)=\frac{1}{1+e^{-z}} \end{aligned}\)

　　则

\( \begin{aligned} g^{'}(z)&=\frac{1}{(1+e^{-z})^2}{e^{-z}}\\&={\frac{1}{1+e^{-z}}}{\frac{e^{-z}}{1+e^{-z}}}\\&=g(z)(1-g(z)) \end{aligned} \) 

　　此函数应用甚广，神经网络的激励函数，独立成分分析中源信号分布都是使用该函数的。

　　假设2个类分别为0和1，回归结果\( h_\theta(x) \)表示样本属于类1的概率，因此样本属于类0的概率则为\( 1- h_\theta(x) \)，则有

\( P(y=1|x,\theta)=h_\theta(x) \)

\( P(y=0|x,\theta)=1-h_\theta(x) \)

　　实际上就是一个两点分布，可写为

\( P(y|x,\theta)=h_\theta(x)^y(1-h_\theta(x))^{1-y} \)

　　从而给定样本集，其对数似然函数为：

\(\begin{aligned} l(\theta)&=log(L(\theta))\\&=log(\prod_{i=1}^m{h_\theta(x^{(i)})^{y^{(i)}}(1-h_\theta(x^{(i)}))^{1-y^{(i)}}})\\&=\sum_{i=1}^m{(y^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)})log(1-h_\theta(x^{(i)})))} \end{aligned}\)

　　最大化该对数似然函数，也采用梯度下降法，下面对其求导。

　　首先有

\(\begin{aligned} \frac{\partial logh_\theta(x^{(i)})}{\partial\theta_j}&=\frac{\partial log(g(\theta^T x^{(i)}))}{\partial\theta_j}\\&=\frac{1}{g(\theta^T x^{(i)})}{ g(\theta^T x^{(i)})) (1-g(\theta^T x^{(i)}))x_j^{(i)}}\\&=(1- g(\theta^T x^{(i)}))) x_j^{(i)}\\&=(1-h_\theta(x^{(i)}))x_j^{(i)} \end{aligned}\)

　　类似可得

\(\begin{aligned} \frac{\partial(1-logh_\theta(x^{(i)}))}{\partial\theta_j}=-h_\theta(x^{(i)})x_j^{(i)} \end{aligned}\)

　　因此有：

\(\begin{aligned} \frac{\partial l(\theta)}{\partial\theta_j}&=\sum_{i=1}^m{(y^{(i)}(1-h_\theta(x^{(i)}))x_j^{(i)}+(1-y^{(i)})(-h_\theta(x^{(i)})x_j^{(i)}))}\\&=\sum_{i=1}^m{(y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)}} \end{aligned}\)

　　由于这里是最大化对数似然函数，故迭代规则为：

\(\begin{aligned} \theta_j=\theta_j+\alpha\frac{\partial l(\theta)}{\partial\theta_j} \end{aligned}\)

　　同样地，这里也有批量梯度下降和随机梯度下降两种实现方法。

 

算法实现

---

　　仔细对比，该迭代公式与线性回归是一样的，但其中的区别在于\(h_\theta(x^{(i)}) \)这个函数是不同的。因此，二者的算法实现可重用代码，只需更改\(h_\theta(x^{(i)}) \)的实现即可。

顺便提一下，在线性回归和逻辑回归的推导中， \(\theta^Tx\)中的常数项为\(\theta_0\)，但由于matlab数组下标从1开始，因此程序中常数项\(\theta_{n}\)其中\(x\)为\(n-1\)维的。

　　具体代码如下，可兼容线性回归与逻辑回归，通过参数传入切换即可：

%返回值Theta为回归结果
%IterInfo为迭代的中间过程信息，用于调试，查看
%Sample为训练样本，每一行为一个样本，每个样本最后一个为Label值
%Type为回归算法类型，'Linear'--线性回归， 'Logistic'--逻辑回归
%BatchSize为每次批量迭代的样本数
function [Theta, IterInfo]=Regression(Sample, Type, BatchSize)
    if strcmpi(Type, 'Linear')
        fun = @Linear;
    elseif strcmpi(Type, 'Logistic')
        fun = @Sigmod;
    else
        return;
    end
    [m, n] = size(Sample); %m个样本，每个n维
    Y = Sample(:, end); %label
    X = [Sample(:,1:end-1), ones(m,1)]';%x加入常数项1，并转换为每列表示1个样本
    
    %将样本顺序随机打乱
    ord = randperm(m);
    X = X(:, ord);
    Y = Y(ord);
    
    BatchSize = min(m, BatchSize);
    Theta = zeros(n, 1);
    Theta0= Theta;
    Alpha = 1e-2 * ones(n, 1);
    StartID = 1;
    
    IterInfo.Grad = [];
    IterInfo.Theta = [Theta];
    
    %梯度下降，迭代求解
    MaxIterTime = 5000;
    for i = 1:MaxIterTime
        EndID = StartID + BatchSize;
        if(EndID > m) 
            TX = [X(:, StartID:m) X(:, 1:EndID-m)];
            TY = [Y(StartID:m); Y(1:EndID-m)];
        else
            TX = X(:, StartID:EndID);
            TY = Y(StartID:EndID);
        end
        
        Grad = CalcGrad(TX, TY, Theta, fun);  

        Theta = Theta + Alpha .* Grad;
        
        %记录中间结果
        IterInfo.Grad = [IterInfo.Grad Grad];
        IterInfo.Theta = [IterInfo.Theta Theta];
        
        %迭代收敛检验
        Delta = Theta - Theta0;
        if(Delta' * Delta < 1e-10)
            break;
        end
        
        Theta0 = Theta;
        StartID = EndID + 1;
        StartID = mod(StartID, m) + 1;
    end
    
    IterInfo.Time = i;
end

%梯度计算
function Grad = CalcGrad(X, Y, Theta, fun)    
    D = 0;
    for i = 1:size(X,2)
        h = fun(Theta, X(:,i));
        G = (Y(i) - h) * X(:,i);
        D = D + G;
    end
    Grad = D / size(X,2);
end

%线性函数
function y = Linear(Theta, x)
    y = Theta' * x;
end

%逻辑回归函数
function y = Sigmod(Theta, x)
    t = Theta' * x;
    y = 1 / (1 + exp(-t));
end

 

　　测试代码中绘制结果部分会有所不同，首先生成测试样本数据的代码如下：

        N = 100;
        %生成第0类数据
        mu = [2 2];
        Sigma = [1 .5; .5 2]; R = chol(Sigma);
        x = repmat(mu,N,1) + randn(N,2)*R;
        y = zeros(N,1);
        Sample = [x y];
        figure, plot(x(:,1),x(:,2),'ro'); hold on
        %生成第1类数据
        mu = [5 6];
        Sigma = [2 1.5; 1.5 3]; R = chol(Sigma);
        x = repmat(mu,N,1) + randn(N,2)*R;
        y = ones(N,1);
        Sample = [Sample;x y];
        plot(x(:,1),x(:,2),'g*');
        save('log_data.mat', 'Sample')

　　生成的两类数据为二维平面上服从不同高斯分布的点，如图：

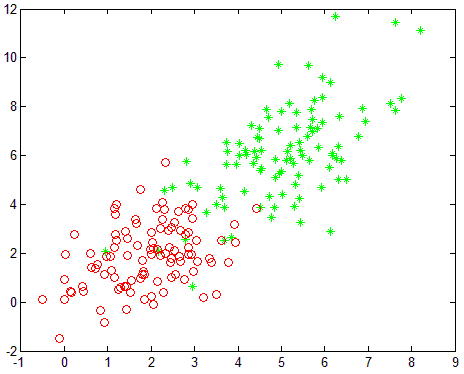
　　测试代码调用比较简单，后面部分为绘制训练结果。

function test
   %回归
    load('log_data.mat');

    BatchSize = 20;   
    [Theta, IterInfo] = Regression(Sample, 'Logistic', BatchSize)
    
    %显示结果，以下代码不通用，样本维数增加时显示不可用
    figure,
    idx = find(Sample(:,3)==1);
    plot(Sample(idx,1), Sample(idx,2), 'g*');hold on
    idx = find(Sample(:,3)==0);
    plot(Sample(idx,1), Sample(idx,2), 'ro');hold on
 
    %显示回归训练的分割线
    x = min(Sample(:,1)):1:max(Sample(:,1));
    y = -(Theta(1) * x + Theta(3))/Theta(2);
    plot(x,y,'b');
     
   %显示对数似然函数的变化
    for i = 1:size(IterInfo.Theta,2)    
        l(i) = L(Sample, IterInfo.Theta(:,i));       
    end
    figure,plot(l,'b');     
end

%似然函数计算
function l = L(Sample, Theta)
    [m, n] = size(Sample); %m个样本，每个n维
    Y = Sample(:, end); %label
    X = [Sample(:,1:end-1), ones(m,1)]';%x加入常数项1，并转换为每列表示1个样本
    l = 0;
    for k = 1:m
        h = 1 / (1 + eps(-Theta' * X(:,k)));
        z = Y(k) * log(h + eps) + (1 - Y(k)) * log(1 - h + eps);
        l = l + z;
    end
end

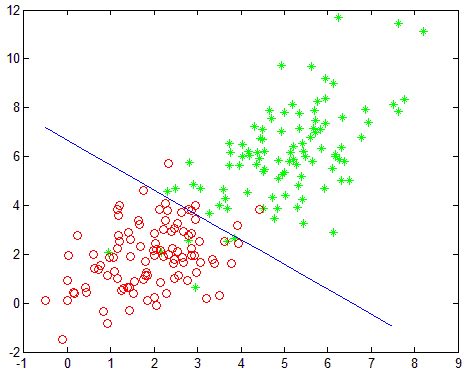
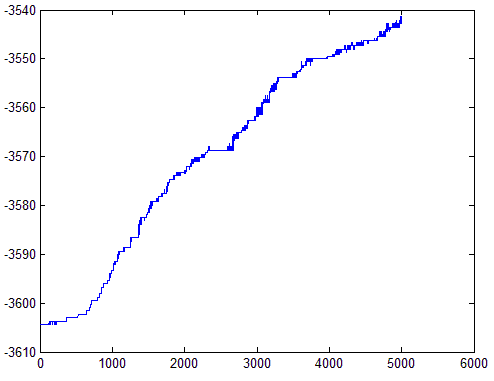
　　实验结果如下，左红绿点分别为两类的训练样本点，图中蓝色直线即是逻辑回归训练处出的分割线。右图为对数似然函数随着迭代过程的变化。

                       

 

算法分析

---

　　1.关于BatchSize的影响与线性回归相同。但在此段代码中，增加了将样本顺序打乱的操作，在逻辑回归中，若正负样本未交叉排列，则使用随机梯度下降时可能导致快速收敛到非最佳解。

　　2.从逻辑回归公式以及上面实验结果可以看到，逻辑回归只能处理线性可分的分类，对于非线性可分问题，需自行转换为线性可分问题来处理。

　　3.上述逻辑回归算法推导与线性回归推导似乎完全不同，但实质上线性回归也可使用类似的最大似然估计来推导，不过对于其值y的假设为高斯分布而已。另外最大似然估计在ML的很多算法中都在使用，需要特别关注下。