JS算法之A*(A星)寻路算法
今天写一个连连看的游戏的时候,接触到了一些寻路算法,我就大概讲讲其中的A*算法。
这个是我学习后的一点个人理解,有错误欢迎各位看官指正。
寻路模式主要有三种:广度游戏搜索、深度优先搜索和启发式搜索。
广度优先搜索(Breadth First Search):又称为"宽度优先搜索"或"横向优先搜索",简称BFS。
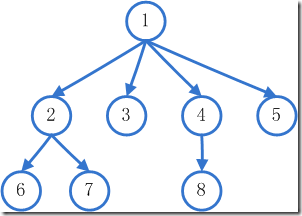
BFS的搜索模式是:从图中某节点v出发,在访问了v之后依次访问v的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使得先被访问的节点的邻接点先于后被访问的节点的邻接点被访问,直至图中所有已被访问的节点的邻接点都被访问到。如果此时图中尚有节点未被访问,则需要另选一个未曾被访问过的节点作为新的起始点,重复上述过程,直至图中所有节点都被访问到为止。
就像这张图,节点1先访问完他相邻的节点2 3 4 5,然后再访问先被访问的节点2,直至节点2的相邻点都被访问完了再接着访问节点4(中间会判断节点3有没有相邻点)。
深度优先搜索(Depth First Search):简称DFS。
DFS的搜索模式是:从某个节点v出发,首先访问该节点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的节点都被访问到。 若此时尚有其他节点未被访问到,则另选一个未被访问的节点作起始点,重复上述过程,直至图中所有节点都被访问到为止。 深度优先搜索是一个递归的过程。
以这图为例,访问顺序是图中的标号。

启发式搜索:启发式搜索就是在状态空间中的访问对每一个访问的位置进行评估,得到最好的位置,再从这个位置进行访问直到目标。启发式算法有很多,例如蚁群算法、遗传算法和模拟退火算法等,其中A*寻路算法就属于启发式算法。
A*估价函数
A*算法最重要的就是他的A*估价函数,用来评估哪个节点离目标点最近,用f(n) = g(n) + h(n)来表示。
f(n)是n节点的估价函数;
g(n)是初始点到n节点的实际代价;
h(n)是n节点到目标点的实际代价;
实际代价可以简单理解为两节点的距离(不同的场景实际代价所表示的意义有所不同)。
估价算法根据各自的需求有很多种,计算距离的估价算法主要的就是曼哈顿算法、几何算法和对角算法。
//曼哈顿估价法
private function manhattan(node:Node):Number
{
return Math.abs(node.x - _endNode.x) * _straightCost + Math.abs(node.y + _endNode.y) * _straightCost;
}
//几何估价法
private function euclidian(node:Node):Number
{
var dx:Number=node.x - _endNode.x;
var dy:Number=node.y - _endNode.y;
return Math.sqrt(dx * dx + dy * dy) * _straightCost;
}
//对角线估价法
private function diagonal(node:Node):Number
{
var dx:Number=Math.abs(node.x - _endNode.x);
var dy:Number=Math.abs(node.y - _endNode.y);
var diag:Number=Math.min(dx, dy);
var straight:Number=dx + dy;
return _diagCost * diag + _straightCost * (straight - 2 * diag);
}
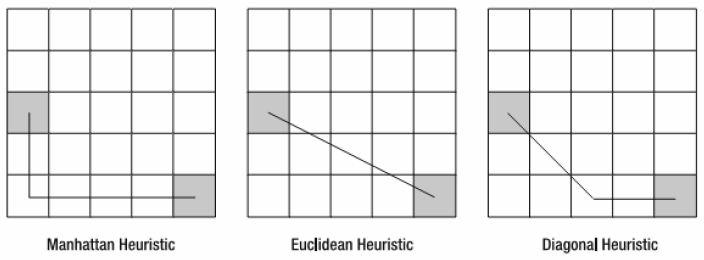
曼哈顿算法是根据网格走直线,直到目标点所在的水平或垂直平行就拐弯;
几何算法实际上就是通过勾股定理,计算两点间的直线距离;
对角算法结合了以上二种算法,先按对角线走,一直走到与目标点水平或垂直平行后,再笔直的走。
Open和Closed列表
open列表:用来记录当前节点所有可能访问的节点;
closed列表:用来记录估价后被否决掉的节点,以后就不用再对这些节点估价了;
工作原理
有了上面基本认识后,现在大概介绍一下A*算法的工作原理。
- 把与当前节点相邻的节点加入到open列表(若非起始结点,则不包括被上一个节点加入到closed列表的节点);
- 算出open列表里所有节点的估价函数f(n)值(总实际代价),得出最小的节点并移动到该节点,还原(清空)open列表;
- 把第2步否决掉的节点记录到closed列表中;
这样就选出了在与当前节点相邻的节点中,离目标节点最近的节点,然后重复123步骤,直到下一个节点为目标节点。