HDU 1227 Fast Food

Fast Food

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 1464    Accepted Submission(s): 633

Problem Description

The fastfood chain McBurger owns several restaurants along a highway. Recently, they have decided to build several depots along the highway, each one located at a restaurant and supplying several of the restaurants with the needed ingredients. Naturally, these depots should be placed so that the average distance between a restaurant and its assigned depot is minimized. You are to write a program that computes the optimal positions and assignments of the depots. 
To make this more precise, the management of McBurger has issued the following specification: You will be given the positions of n restaurants along the highway as n integers d1 < d2 < ... < dn (these are the distances measured from the company's headquarter, which happens to be at the same highway). Furthermore, a number k (k <= n) will be given, the number of depots to be built. 
The k depots will be built at the locations of k different restaurants. Each restaurant will be assigned to the closest depot, from which it will then receive its supplies. To minimize shipping costs, the total distance sum, defined as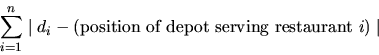must be as small as possible.
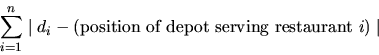
Write a program that computes the positions of the k depots, such that the total distance sum is minimized. 

 

 

Input

The input file contains several descriptions of fastfood chains. Each description starts with a line containing the two integers n and k. n and k will satisfy 1 <= n <= 200, 1 <= k <= 30, k <= n. Following this will n lines containing one integer each, giving the positions di of the restaurants, ordered increasingly.
The input file will end with a case starting with n = k = 0. This case should not be processed. 

 

 

Output

For each chain, first output the number of the chain. Then output a line containing the total distance sum. 
Output a blank line after each test case.

 

 

Sample Input

6 3

5

6

12

19

20

27

0 0

 

 

Sample Output

Chain 1

Total distance sum = 8

 

 

Source

Southwestern Europe 1998

 

 

Recommend

JGShining

 

 

 

转：

在n个商店中建m个仓库，使各个商店到仓库的路程之和最小，商店到哪个仓库是有选择的，

总之路程之和要最小！

 

我还以给的例子来说，这道题的具体思路：

本来想做个图的，这样更清晰，我辛苦做出来的弄上面无法显示啊！我泪奔啊，我只能用汉字来说了，考验一下额的汉字表达水平！

• 仓库要建在商店的位置，也就是说，它一定在某个商店的坐标处；

首先：

我们可以将一下n个商店的位置存入dis[]数组（这里注意，这里说的是位置，我们可以想象，highway当做一个数轴来看，那么dis[i]就代表第i个商店在数轴上的坐标，就是位置，它不代表距离）；

然后：

我们要算出从第i个商店到第j个商店之间建一个仓库之后又增加的距离case[i][j]，这里要明白，从第i个商店到第j个商店建一个仓库，这个仓库所建的位置一定是dis[(i+j)/2],即建在它的中位数处，所以，这个增加值就是case[i][j]=abs(dis[k]-dis[(i+j)/2])(i<=k<=j);

接下来找dp[i][j];dp[i][j]代表前j个商店建i个仓库的最小距离；

下面就是最难理解的一步了，动态转移方程的寻找，

不好理解就在于有多个阶段，每个阶段都有多个状态，每个阶段的初始值都是不确定的，我们要把它初始为一个尽可能大的数，要找dp[i][j],首先dp[i][j]=10000000（尽可能的大）；然后找前一个状态，dp[i-1][m]

为啥是m呢？因为，上一个状态的仓库数是一定的，肯定是比该状态少1，但是商店数就是不确定的了，它最小是

i-1，最大是j-1,即m的范围就是(i-1<=m<=j-1)，找到上个状态后，再加上一个增加值，这个增加值是从m+1

到j之间建一个仓库所增加的距离，即case[m+1][j];该状态是dp[i-1][m]+case[m+1][j];那么dp[i][j]就是两值得最小，每次m的改变就会将最小的存入dp[i][j]，最后一次的更新，得到该状态的最小值；

这样，我们就找到了状态转移方程

dp[i][j]=MIN(dp[i-1][m]+case[m+1][j]),(i-1<=m<=j-1);

 

 

#include<stdio.h>
#include<string.h>

const int maxn=220;
const int INF=99999999;

int dis[maxn],dp[maxn][maxn],cost[maxn][maxn];

int abs(int x){
    return x<0?-x:x;
}

int min(int a,int b){
    return a<b?a:b;
}

int main(){

    //freopen("input.txt","r",stdin);

    int n,k;
    int cases=0;
    while(scanf("%d%d",&n,&k)){
        int i,j,m;
        if(n==0 && k==0)
            break;
        for(i=1;i<=n;i++)
            scanf("%d",&dis[i]);
        for(i=1;i<=n;i++)
            for(j=i;j<=n;j++){
                cost[i][j]=0;
                for(m=i;m<=j;m++)
                    cost[i][j]+=abs(dis[m]-dis[(i+j)/2]);
            }
        for(i=1;i<=n;i++)
            dp[1][i]=cost[1][i];
        for(i=2;i<=k;i++)
            for(j=i;j<=n;j++){
                dp[i][j]=INF;
                for(m=i-1;m<=j-1;m++)
                    dp[i][j]=min(dp[i][j],dp[i-1][m]+cost[m+1][j]);
            }
        printf("Chain %d\nTotal distance sum = %d\n\n",++cases,dp[k][n]);
    }
    return 0;
}