神经网络学习笔记

神经网络是使用代码模拟生物神经系统，由具有适应性简单元组成的广泛并行互联网络。

 

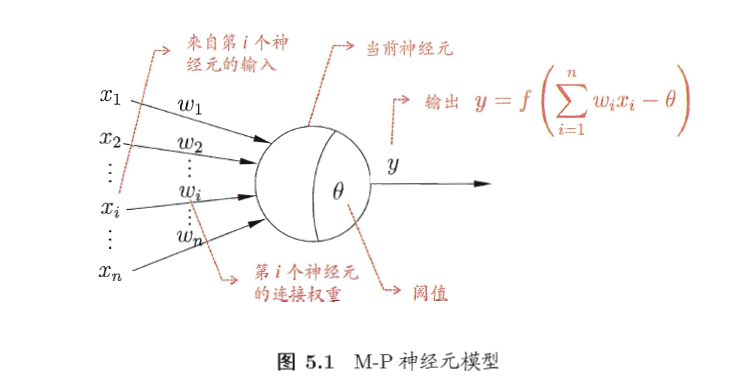
x1 x2 xi ... xn为输入

w1 w2 wi... wn为对应输入的权值

所有输入乘以权值的和 与 阈值对比

然后通过激活函数进行输出值的处理

一般直觉上来说输出值就为0或者1 对应计算机里的真假概念

函数图像如图

但是这种处理方法处理过于简单 非黑即白 函数不连续不光滑

所以会使用Sigmoid函数代替

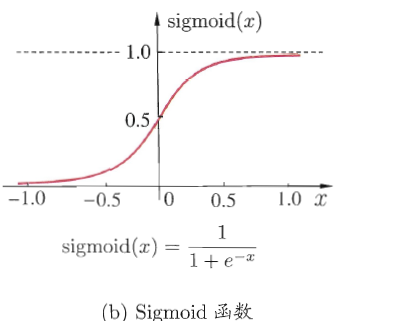
这样函数就会平滑许多而且输出的大部分范围在 (-1.0 , 1.0)之间

 

先来看一个两层神经元的感知机 激活函数是阶跃函数

 

使用它来表示

与或非中的与示例

正确的与示例 输入与输出应该是这样

x1     x2      y

1       1       1

0       0       0

1       0       0

0       1       0

这里对神经元的参数进行一个随机初设

w1 = 1 w2 = 1  阀值为1

那么 对于 x1 = 1 x2= 1的输入 则是

y= f(1*1 + 1 *1 -1) = f(1) = 1 (阶跃函数中 输入大于等于0的值 输出值为1)

与预想结果相同 不做调整

 

对于 x1 = 0   x2= 0的输入 则是

y= f(0*1 + 0 *1 -1) = f(-1) = 0 (阶跃函数中 输入小于0的值 输出值为0)

与预想结果相同 不做调整

 

对于 x1 = 1   x2= 0的输入 则是

y= f(1*1 + 0 *1 -1) = f(0) = 1 (阶跃函数中 输入大于等于0的值 输出值为1)

与结果就不一样了 这个时候就需要进行调整

根据式 5.2

权值调整

△w1 = 0.1(0-1)1 = -0.1

△w2 = 0.1(0-1)0 = 0

那么 w1+△w1 = 0.9 

w2 + △w2 = w2 不变

对于 x1 = 1   x2= 0的输入 则是

y= f(1*0.9 + 0 *1 -1) = f(-0.1) = 0 (阶跃函数中 输入小于0的值 输出值为0)

调整完毕

 

对于 x1 = 0   x2= 1的输入 则是

y= f(0*0.9 + 1 *1 -1) = f(0) = 1 (阶跃函数中 输入等于0的值 输出值为1)

与结果不一致 需要调整

△w1 = 0.1(0-1)0 = 0

△w2 = 0.1(0-1)1 = -0.1

 

w1+△w1 = 0.9+0 = 0.9

w2+△w2 = 1 - 0.1 = 0.9

对于 x1 = 0   x2= 1的输入 则是

y= f(0*0.9 + 1 *0.9 -1) = f(-0.1) = 0

系统调整完毕

 

最终结果

w1 =0.9  w2 = 0.9 阀值=1  

阶跃函数

 

可正确计算 与计算

 

 

 

 

笔记中可能存在学习过程中的错误理解 仅供参考

截图来自 《机器学习》 作者周志华